【基本】一次方程式の利用（速さ）

ここでは、一次方程式を利用して解く問題を見ていきます。速さに関連する問題を見ていきます。

追いかける問題

速さに関する問題です。苦手な人も多いかもしれませんが、基本的には使う関係は次の式だけです。

　速さ × 時間 = 距離

この問題では、速さがわかっています。時間については、「弟の出発の10分後に兄が出発」ということしかわかりません。しかも、距離については、何もわかりません。この状態では、解ける気がしませんね。

わからないことが多いので、仮の話をして、少し様子を見てみましょう。例えば、兄が家を出発してから5分後の状況を考えてみましょう。このとき、二人はどこにいるでしょうか。

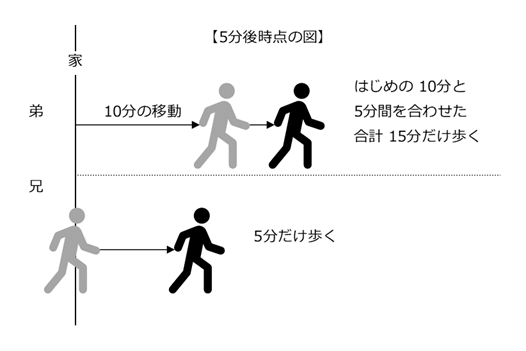
まず、弟は、10分間、先に歩いているので、合計で15分歩いていることになります。なので、家から\[ 50 \times 15=750 \]m離れたところにいることがわかりますね。一方、兄が歩いたのは5分だけなので、\[ 70 \times 5=350 \]m離れたところにいることがわかります。まだまだ追いついていませんね。

ところで、「追いつく」とはどのような状況でしょうか。少し考えると、兄が弟に追いついたとき、二人は、家から同じだけ離れたところにいることがわかります。

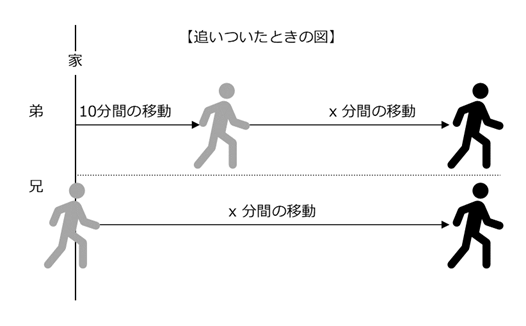
ということは、先ほどの例で「5分後」としていたところを「 $x$ 分後」に変え、「二人の歩いた距離が等しい」という関係を方程式で表せばよさそうですね。以上を踏まえると、次のような解答になります。

実際、25分後には、弟は $50\times(25+10)=1750$ m 進んでいることがわかります。一方、兄は、 $70\times 25 = 1750 $ m 歩くことになり、たしかに追いついていることがわかります。なお、後半に出てくる「これは問題にあっている」は、後に出てくる別ページで説明します。

往復する問題

自転車を撤去された経験がない人にはわかりにくいかもしれませんが、単純に、2つの地点を往復する問題だと考えてもらってかまいません。

ここでも使う関係式はこれです。

　速さ × 時間 = 距離

今回は、距離を求めなさいと言われています。速さはわかっています。が、時間がわかりません。往復でかかった時間はわかりますが、それぞれでかかった時間はわかりません。

何に注目するかで、方程式の作り方は異なってきます。まず、行きにかかった時間を $x$ 時間とする方法があります。この場合、帰りにかかった時間は、 $(3-x)$ 時間ですね。行きも帰りも、距離は同じなので、\[ 4\times x=12(3-x) \]という方程式が成り立ちます。これを解いて
\begin{eqnarray} 4x &=& 12(3-x) \\[5pt] 4x &=& 36-12x \\[5pt] 16x &=& 36 \\[5pt] x &=& \frac{9}{4} \\[5pt] \end{eqnarray}となります。行きにかかった時間がわかったので、距離は\[ 4\times\dfrac{9}{4}=9 \]kmだと求められます。

一方、距離を聞かれているのだから、素直に距離を文字で置く方法もあります。自転車の保管場所までの距離を $x$ kmとすると、行きにかかった時間は $\dfrac{x}{4}$ 時間、帰りの時間は $\dfrac{x}{12}$ 時間です。この和が $3$ 時間なのだから、\[ \frac{x}{4}+\frac{x}{12}=3 \]という方程式が成り立ちます。これを解いて
\begin{eqnarray} \frac{x}{4}+\frac{x}{12} &=& 3 \\[5pt] 3x+x &=& 36 \\[5pt] x &=& 9 \\[5pt] \end{eqnarray}となります。こうして、距離が $9$ km だと求めることができます。

おわりに

ここでは、速さに関する、一次方程式の問題を見てきました。速さに関する問題では、時間や距離とからめて考えることになります。このページで見た問題では、「兄と弟の移動距離が等しい」「行きと帰りの移動距離が等しい」という距離に関する関係や「行きと帰りに掛かった時間は3時間」という時間に関する関係をもとに方程式を作っています。等しいものがないかを考えて、方程式を作るようにしましょう。