【基本】一次方程式の利用（ものを配る）

ここでは、一次方程式を利用して解く問題を見ていきます。ものを配ることに関連する問題を見ていきます。

子どもの人数を文字で置く

このページでは、次のような問題を考えます。

この問題では、わからないものが2つあります。子どもの人数と折り紙の枚数ですね。

【基本】一次方程式の利用（差を利用） や 【基本】一次方程式の利用（和を使う）では、わからないものが2つありました。ただ、これらの問題では、「片方がわかれば残りもすぐにわかる」という状況でした。今回は、片方がわかっても、残りはそう簡単にはわかりません。なので、少し難しいですね。

問題を解く手がかりは、2つあります。「1人に3枚ずつ配ると16枚余る」「1人に4枚ずつ配ると2枚足りない」ですね。これらをヒントに、子どもの人数と折り紙の枚数の関係を考えてみましょう。

仮に、子どもの数が5人だったとしてみます。このときに折り紙の枚数がどうなるかを考えてみましょう。

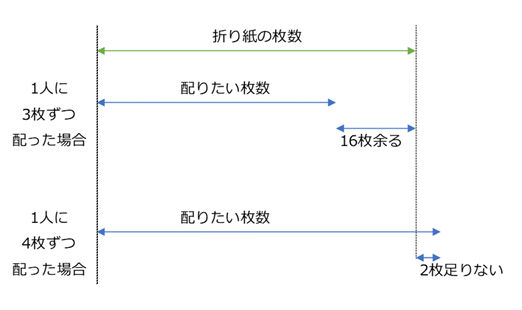
1人3枚ずつ配ると16枚折り紙が余るので、この状況をもとに折り紙の枚数を計算すると\[ 3\times5+16=31 \]枚となります。一方、4枚ずつ配ると2枚足りないので、折り紙の枚数は\[ 4\times5-2=18 \]枚となります。2つの結果が同じではないので、折り紙の枚数のつじつまが合いません。なので、子どもの数が5人だとすると、条件を満たさないことがわかります。

逆にいうと、この2つの計算結果が同じなら、折り紙の枚数についてはつじつまがあうということですね。つまり、「3を掛けて16を足した数」と「4を掛けて2を引いた数」が同じになる場合を考えればいいことになります。これは、方程式で表すことができますね。

子どもの人数を $x$ 人とすれば、折り紙の枚数は $(3x+16)$ 枚であり、 $(4x-2)$ 枚とも書けるので、\[ 3x+16=4x-2 \]が成り立ちます。これを解けば、答えが得られます。解答は以下のようになります。

今までも、「あるものを2通りで表す」ことで方程式を作っていましたが、今まではもっと簡単でした。上のリンク先では、「みかんとりんごを買ったら1200円だった」というような問題を考えましたが、その問題では「みかんの代金 + りんごの代金 = 1200」という式を作りました。問題文を読めば、どんな式を作ればいいかはわかりやすかったです。

一方、この例題では、折り紙の枚数を2通りで表すことで、方程式を作りました。今回は、問題文を読んでも、どんな式を作ればいいかは、すぐにはわからなかったかもしれません。しかし、「同じものを2通りで表す」という方針は同じです。同じものを2通りで表せば、方程式ができ、わからなかったものを求めることができます。

2通りで表せるものはないか、を考えるようにしましょう。

なお、後半に出てくる「これは問題にあっている」は、後に出てくる別ページで説明します。

折り紙の枚数を文字で置く

先ほどの例題を、別の角度から考えてみましょう。

先ほどは、子どもの人数を $x$ で置いて、折り紙の枚数を2通りで表しました。一方で、折り紙の枚数を $x$ で置いて、子どもの人数を2通りで表す解き方もあります。この方法を見ていきましょう。

折り紙の枚数を $x$ 枚とします。まずは、1人に3枚ずつ配る場合を考えましょう。このときの子どもの人数はどのような式で表すことができるでしょうか。3枚ずつ配ると16枚余ったのだから、逆にいうと、16枚引けば、過不足なく配れるということですね。なので、 $(x-16)$ 枚であれば、3枚ずつ配るとちょうどみんなに配れることがわかります。

同様に考えると、1人に4枚ずつ配る場合は、2枚足りないのだから、2枚増やせば過不足なく配れることがわかります。よって、 $(x+2)$ 枚なら、4枚ずつ配るとみんなに配れます。

これらのことから、子どもの人数は、 $\dfrac{x-16}{3}$ とも $\dfrac{x+2}{4}$ とも書けることがわかります。これを用いて方程式を作ることもできます。解答は次のようになります。

最後に子どもの人数を求めるときに、 $\dfrac{x-16}{3}$ の式に代入していますが、 $\dfrac{x+2}{4}$ に代入しても構いません。方程式の解は、この2つが同じになるような値なので、どちらに代入しても、子どもの人数は18人となります。

おわりに

ここでは、一次方程式を使って、ものを配る問題を解く方法を見てきました。何人に配るか、何個を配るか、どちらを基準にしても方程式を作ることができます。同じものを2通りで表すことを考えるようにしましょう。