【基本】微分係数と導関数（の復習）

ここでは、昔学んだ微分係数や導関数のことを振り返りながら、内容をまとめていきます。

微分係数の復習

昔学んだ「微分」の内容について振り返っていきましょう。

もともとは、【導入】微分を考える意味についてで見たように、三次関数やそのグラフを調べるためのツールとして、微分を導入しましょう、という話をしました。一次関数や二次関数のグラフのときとは異なり、いくつかの点をとって線をつなげても、正しいグラフが得られないケースがありました。

例えば、 $y=2x^3-x$ のグラフは、 $(0,0)$, $(1,1)$, $(2,14)$, $(3,51)$ といった点を通りますが、これらをなめらかにつないだもの（下の図の破線）は、正しいグラフ（赤線）とは異なってしまいます。

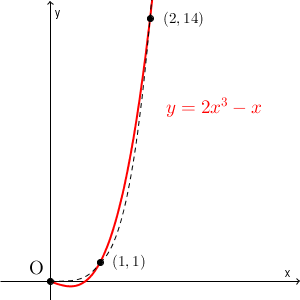
いくつかの点をとってなめらかにつないだだけでは、谷の部分があったことに気づけません。 $x$ の変化幅が大きすぎたんですね。

そこで、【基本】微分係数や【基本】極限値と微分係数で見たように、少し考え方を変えたのでした。 $x$ をちょっと動かしたときに、関数 $f(x)$ がどのくらいの割合で変化するかを考えることにしたんですね。このときの $x$ の変動幅は、大きすぎると、先ほどのように谷などの重要情報を見過ごしてしまうからダメなのですが、逆にどれくらい小さくすればいいのかはわかりません。なので、限りなく小さくする、つまり、極限を考えることにしたのでした。このときの極限を微分係数(derivative) というのでしたね。

この右辺の分母が $x$ の変動幅、分子が関数の変動幅に対応しています。この割合を平均変化率といい、この極限をとったものが微分係数です。

右辺の式は、 $a+h=x$ とおいて、次のように書くこともあります。置き換えているだけで、まったく同じ式です。\[ f'(a)=\lim_{x\to a} \dfrac{f(x)-f(a)}{x-a} \]

どんな関数、どんな（定義域内の）値に対しても、微分係数が存在するとは限りません。もし、ある関数 $f(x)$ について、 $x=a$ で微分係数が存在する場合は、 $f(x)$ は $x=a$ で微分可能 といいます。

【基本】微分と接線の方程式で見たように、この「微分係数」は、図形的には、接線の傾きを表しています。下の図を見てみましょう。

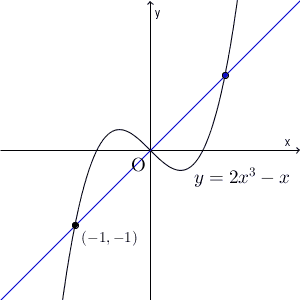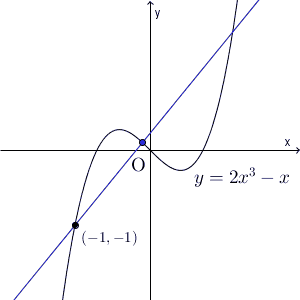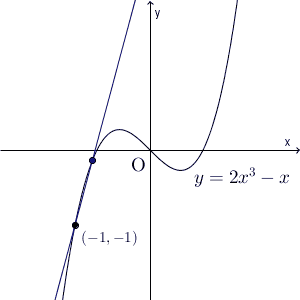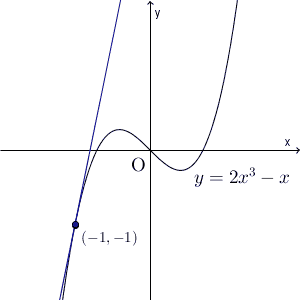
2点をつなぐ直線の傾きが平均変化率で、この2点の距離を限りなく近づけると、点 $(a,f(a))$ を通る、傾きが $f'(a)$ の直線に近づいていきます。この直線のことを接線といいます。

導関数の復習

先ほどは「 $x=a$ での微分係数」を考えましたが、ここでは、この $a$ をいろいろ動かしてみることを考えていきます。ここで見る内容は、【基本】導関数の復習です。

関数 $f(x)$ が $x=a$ で微分可能なら、 $f'(a)$ が存在するのでしたね。このとき、 $a$ に対して $f'(a)$ を対応させる、という関数を考えることができます。この関数のことを導関数(derivative function) といいます。

ある区間のすべての $x$ の値で微分可能であるとき、「 $f(x)$ はその区間で微分可能」といいます。定義域全体で微分可能なら、単純に「微分可能」といいます。

また、関数 $f(x)$ から導関数 $f'(x)$ を求めることを「 $f(x)$ を微分する」といいます。

通常、 $y=f(x)$ の導関数は $f'(x)$ と表しますが、 $y'$ と書くこともあります。また、\[ \dfrac{dy}{dx},\ \dfrac{d}{dx}f(x) \]といった書き方をすることもあります（参考：【標準】導関数のいろいろな表し方）。

なぜ微分係数と導関数の復習をするのか

さて、なぜ今頃になって、微分係数や導関数、微分のことについて復習をするかというと、これから微分する対象の関数を増やしていきたいからなんですね。

過去に微分に学んだときには、主に三次関数を微分しました。今後は、もっと様々な関数、例えば、無理関数や分数関数、三角関数や指数関数・対数関数の微分などを考えていきます。微分というのは、極限の一種であり、いろんな関数の極限について学んだ（参考：関数と極限）ので、今となっては、微分の計算ができる対象が増えたわけなんですね。なので、改めていろんな関数に対して、微分を考えていこう、というわけです。

おわりに

ここでは、微分係数、導関数、微分などについての復習を行いました。今後、いろんな関数を微分することができるようになることで、複雑な数式で書かれた関数の微分が計算できたり、グラフがかけたり、いろいろな不等式が証明できたりと、できることの範囲が急激に広がっていきます。三次関数の微分を学んでいたときよりも、さらに「微分」の世界のすごさがわかってくると思います。