【導入】微分を考える意味について

ここでは、これから新しく見ていく分野「微分」（びぶん）について、なぜ必要なのか、どういうものなのか、というのを、ざっくりと見ていきます。

一次関数、二次関数、と来たら

過去を振り返ってみると、中学の数学で一次関数を習い、その後、中学から高校にかけて、二次関数を習いました。この流れでいくと、三次関数、四次関数も出てくるんだろうな、という予感はしますよね。

しかし、三次関数を調べて、四次関数も調べて…とやっていくと、いつまでも終わりません。次数が上がっても使える「こうやって調べればいい」という手法やツールがあったほうが便利です。

例えば、小学生の時には、はじめに1桁の足し算を学び、次に2桁の足し算を学びました。しかし、その後、3桁、4桁、5桁…の足し算を、1つ1つやっていくことはありませんでした。3桁以上の場合の足し算は、筆算を使えば、計算方法は同じです。なので、1つ1つやっていくことはなかったんですね。「後は同じようにやればいいんだよ」で終わりです。実際、僕たちは10桁同士でも100桁同士でも、直接は習っていないけど、足し算をすることができます（頑張れば）。

関数の場合も、一次、二次とやってきましたが、三次以上の場合は、三次以上のすべての場合に使える新しいツールを導入します。それが、今後見ていく「微分」です。微分を知れば、理論上は、三次以上の関数でも、グラフをかくことができます。

なぜ新しいツールがいるのか

三次以上の関数では、「微分」を導入すると、グラフがかけるようになる、と言いましたが、そもそもなぜ新しいツールがいるのでしょうか。具体例を使って、少し考えてみましょう。

例えば、 $y=2x^3-x$ という三次関数のグラフを考えてみます。一次関数や二次関数の場合は、いくつか点をとってみて、それをつないでグラフをかきました。これによって、一次関数のグラフは直線に、二次関数のグラフは放物線になるのでしたね。同じように、この三次関数の場合もやってみましょう。

$y=2x^3-x$ のグラフが通る点をいくつか計算してみます。とりあえず、 $x\geqq 0$ の部分だけを考えてみると、 $(0,0)$, $(1,1)$, $(2,14)$, $(3,51)$ などとなります。

上過ぎて $(3,51)$ が入っていませんが、これらを緩やかにつなげば、三次関数のグラフになるのかな、と予想できます。

しかし、残念ながらこれは正しくありません。 $y=2x^3-x$ の正しいグラフは、次の赤い線のようになります。

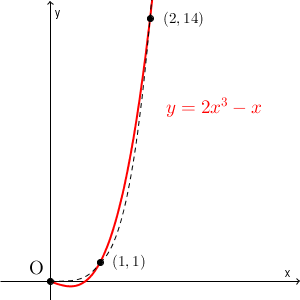
途中に、谷があったんですね。原点のまわりを拡大して全体のグラフをかくと、 $y=2x^3-x$ のグラフは次のようになります。

山も谷もありました。これに気づかずに、 $(-1,-1)$, $(0,0)$, $(1,1)$ をまっすぐにつないでしまうのは、まずいですね。明らかに形が違います。しかし、どうやったら、山や谷があったことに気づけたのでしょうか。

今の場合は、 $2x^3-x=x(2x^2-1)$ なので、 $x=0,\pm\dfrac{\sqrt{2} }{2}$ のときに、この関数のグラフは x 軸と交わることがわかります。3点で交わるから山や谷がある、と判断することができたかもしれません。しかし、 $y=2x^3-x+1$ という関数のグラフだったらどうでしょうか。

x 軸と交わる箇所は1ヶ所です。こうなると、 x 軸と交わる点の個数から、山や谷があることが判断できません。

「三次関数のグラフは、山や谷がいつもあるんじゃないか」と思う人もいるかもしれません。しかし、先ほどの関数で x の部分の符号を変えた関数 $y=2x^3+x$ のグラフを見てみましょう。このグラフは、次のような形になります。

山も谷もありません。

こうしたことから、三次関数の場合は、一次関数や二次関数のときとは違い、「通る点をいくつか求めて、それらをつなぐ」という方法では、グラフをかくことができません。なので、今までにはない、新しいツールが必要となります。

微分があるとどうなるのか

先ほど、三次関数のグラフの場合は、一次関数や二次関数のグラフで考えたような「通る点をいくつか求めてつなぐ」という方法が使えないことを見ました。通る点をいくつか集めても、その間で何が起こっているかがわからないんですね。だから、単純に「つなぐ」ことができません。

$y=2x^3-x$ のグラフを見て、特徴的だなと感じるのは、やはり、山や谷となっている部分でしょう。少なくとも、これがなければ、グラフをかいたとは言えません。

ここで、 x を小さい方から徐々に動かしていったと考えましょう。 $x=-100$ などの小さな値であれば、 y の値もマイナスです。なので、はじめは、左下の方にいます。これを徐々に大きくしていくと、いつかは x 軸を超え、山の頂点までいきます。この間、つねに y の値は増え続けます。山の頂点を超えると、 x が増えるたびに y は減り、谷底へと向かいます。そして、谷底を過ぎれば、 x が増えるたびに、 y は増えるようになっていきます。

つまり、 x を増やしたときに、 y がどう変化するか、ということが、山や谷の情報につながっていることがわかります。「 x を増やしたとき」と書きましたが、この増やし方には注意が必要です。というのも、「 $x=-1$ から $x=0$ と増やせば、 y は増える」となりますが、こう考えてしまうと、この間にある山の情報が消えてしまいます。つまり、x の動かし方はすごく小さくないといけません。

よって、「 x が少し変化したときに、 y がどう変化するか」がポイントなんですね。これがまさに微分の考えです。今後は、この考えをベースに、微分や三次関数のグラフなどについて考えていきます。まずは、【基本】平均変化率について、見ていきましょう。