【基本】円と媒介変数表示

🕒 2018/05/29 🔄 2023/05/01

ここでは、円を媒介変数表示で表すとどうなるかを見ていきます。

📘 目次

一般角を用いた円の媒介変数表示

【基本】媒介変数表示と内容がかぶりますが、一般角を用いた円の媒介変数表示を見ていきましょう。

原点を中心とする半径 $a$ の円の方程式は\[ x^2+y^2=a^2 \]で表されます。この円周上の点を $\mathrm{ P }(x,y)$ とし、点 P は、原点を中心に点 $\mathrm{ A }(a,0)$ を $\theta$ だけ反時計回りに回転した点だとすると
\begin{eqnarray} x &=& a\cos\theta \\ y &=& a\sin\theta \\ \end{eqnarray}が成り立ちます。

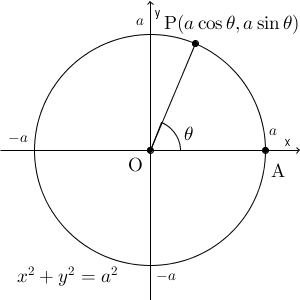
$\theta$ を用いて円周上の点の座標 $(x,y)$ を表すことができているので、これは円の媒介変数表示である、といえます。

このように $\theta$ を使って書くと、次のような場合に便利です。例えば、円周上の点 $(x,y)$ に対して、 $x+y$ が最大になるときを考えてみましょう。 $x,y$ だけで解くこともできますが、上のように $x=a\cos\theta$, $y=a\sin\theta$ と表してから変形すると
\begin{eqnarray} x+y &=& a(\cos\theta+\sin\theta) \\[5pt] &=& \sqrt{2}a \sin\left(\theta+\dfrac{1}{4}\pi\right) \\[5pt] \end{eqnarray}となります。後半では、三角関数の合成を用いています（参考：【標準】三角関数の合成）。

この変形から、 $x+y$ の最大値は $\sqrt{2}a$ であることがすぐにわかります。また、そのとき、 $\theta=\dfrac{1}{4}\pi$ なので、 $x=y=\dfrac{1}{\sqrt{2} }$ のときであることもわかります。

このように、 $x,y$ で考えるよりも、三角関数を用いて表し、三角関数での様々な性質を用いて変形すると、問題が解きやすくなる、というケースがあります。

動く直線と円の媒介変数表示

円の媒介変数表示の例として、直線を使うものも紹介します。

ここでは、単位円 $x^2+y^2=1$ を考えます。 $\mathrm{ A }(-1,0)$ とし、この点を通る傾き $t$ の直線と、単位円との、点A 以外の交点を考えましょう。

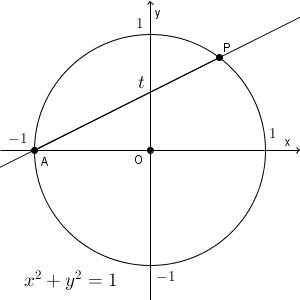
交点を $\mathrm{ P }(x,y)$ とおきます。この直線の方程式は\[ y=t(x+1) \]なので、これを円の方程式に代入して
\begin{eqnarray} x^2+\{t(x+1)\}^2 &=& 1 \\[5pt] x^2-1+t^2(x+1)^2 &=& 0 \\[5pt] (x+1)\{(x-1)+t^2(x+1)\} &=& 0 \\[5pt] (x+1)\{(1+t^2)x +t^2-1\} &=& 0 \\[5pt] \end{eqnarray}となることがわかります。ここで、 $x\ne -1$ なので、\[ x=\dfrac{1-t^2}{1+t^2} \]となります。また、 \begin{eqnarray} y &=& t(x+1) \\[5pt] &=& t \left(\dfrac{1-t^2}{1+t^2}+1\right) \\[5pt] &=& \dfrac{2t}{1+t^2} \\[5pt] \end{eqnarray}となります。

傾きを動かすと、単位円の円周上の点のうち、 $(-1,0)$ を除いた点は、すべて上のように表すことができます。よって、
\begin{eqnarray} x &=& \dfrac{1-t^2}{1+t^2} \\[5pt] y &=& \dfrac{2t}{1+t^2} \\[5pt] \end{eqnarray}は、単位円から $(-1,0)$ を除いた部分の媒介変数表示となります。

ところで、この $t$ は何を表しているかを考えてみましょう。単位円周上の点を $\mathrm{ P }(x,y)$ とし、 x 軸の正の向きと OP とのなす角を $\theta$ とします（反時計回りが正）。このとき、 $\mathrm{ P }(\cos\theta,\sin\theta)$ となりますね。

また、 $t$ は直線 AP の傾きでした。これは $\angle \mathrm{ PAO }$ が $\dfrac{1}{2}\theta$ であることを考えると、\[ t=\tan\frac{1}{2}\theta \]と書けます。

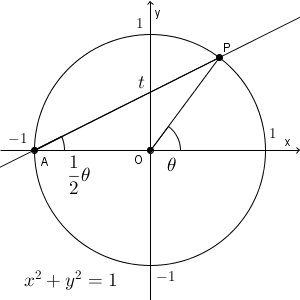
つまり、上の媒介変数表示は、 $\tan\dfrac{1}{2}\theta$ を用いて、 $\cos\theta$, $\sin\theta$ を表していた、と考えることができます。この表し方は、【応用】半角のtanを用いた三角関数の媒介変数表示や【応用】三角関数の媒介変数表示を図形的に考えてみるで取り上げています。

上では $x,y$ の方程式について考えていましたが、リンク先では三角関数（倍角の公式など）について考えていました。別々のアプローチで同じ式にたどりつくのはおもしろいですね。