東京大学 理系 2021年度 第1問 解説
問題編
問題
$a,b$ を実数とする。座標平面上の放物線\[ C:\ y=x^2+ax+b \]は放物線 $y=-x^2$ と2つの共有点を持ち、一方の共有点の $x$ 座標は $-1\lt x\lt 0$ を満たし、他方の共有点の $x$ 座標は $0\lt x\lt 1$ を満たす。
(1) 点 $(a,b)$ のとりうる範囲を座標平面上に図示せよ。
(2) 放物線 $C$ の通りうる範囲を座標平面上に図示せよ。
考え方
(1)は $(a,b)$ の話で、(2)は $(x,y)$ の話なので、よく考えないと頭が混乱してきます。(2)は放物線を直接動かすことを考えるよりも、(1)の結果を利用することを考えましょう。
解答編
問題
$a,b$ を実数とする。座標平面上の放物線\[ C:\ y=x^2+ax+b \]は放物線 $y=-x^2$ と2つの共有点を持ち、一方の共有点の $x$ 座標は $-1\lt x\lt 0$ を満たし、他方の共有点の $x$ 座標は $0\lt x\lt 1$ を満たす。
(1) 点 $(a,b)$ のとりうる範囲を座標平面上に図示せよ。
解答例
(1)
$f(x)=x^2+ax+b-(-x^2)$ とすると、条件より、 $f(x)=0$ は $-1\lt x\lt 0$ を満たす解と $0\lt x\lt 1$ を満たす解を持つ。このグラフは下に凸の放物線なので、 $f(-1)\gt 0$, $f(0)\lt 0$, $f(1)\gt 0$ の3つが同時に成り立つことと同値である。
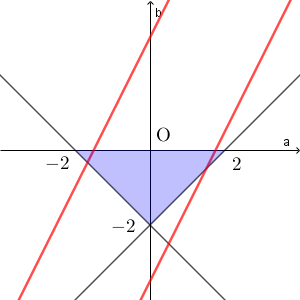
$f(-1)\gt 0$ より $b\gt a-2$ 、 $f(0)\lt 0$ より $b\lt 0$ 、 $f(1)\gt 0$ より $b\gt -a-2$ なので、点 $(a,b)$ のとりうる範囲は次の図の色のついた部分となる(境界線上の点は含まない)。
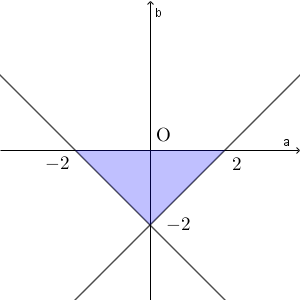
(終)
解答編 続き
問題
(2) 放物線 $C$ の通りうる範囲を座標平面上に図示せよ。
解答例
(2)
$y=x^2+ax+b$ は、 $b=-xa+(y-x^2)$ と変形できる。これを $a$ と $b$ の関係式と考えて $ab$ 平面上にグラフをかき、(1)で求めた範囲と共有点を持つ場合を考えればよい( $x,y$ を決めたときに(1)の範囲と共有点を持てば、対応する $(a,b)$ が存在することを意味し、共有点を持たなければ対応する $(a,b)$ が存在しないことを意味するため)。
なお、 $a$ の関数 $f(a)$ を $f(a)=-xa+(y-x^2)$ で定める。このとき、直線 $b=f(a)$ の傾きは $-x$ である。
(i) $x\gt 1$ の場合
$b=f(a)$ の傾きは $-x\lt -1$ である。
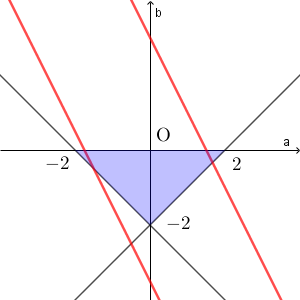
(1)の範囲と共有点を持つことは、 $f(-2)\gt 0$ かつ $f(2)\lt 0$ が成り立つことと同値である。 $f(-2)\gt 0$ より $y\gt x^2-2x$ が得られ、 $f(2)\lt 0$ より $y\lt x^2+2x$ が得られる。
(ii) $0\leqq x \leqq 1$ の場合
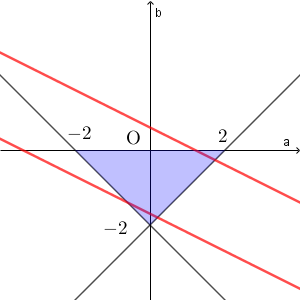
(1)の範囲と共有点を持つことは、 $f(0)\gt -2$ かつ $f(2)\lt 0$ が成り立つことと同値である。 $f(0)\gt -2$ より $y\gt x^2-2$ が得られ、 $f(2)\lt 0$ より $y\lt x^2+2x$ が得られる。
(iii) $-1 \leqq x \lt 0$ の場合
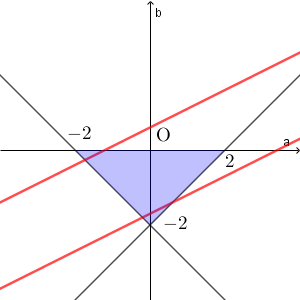
(1)の範囲と共有点を持つことは、 $f(0)\gt -2$ かつ $f(-2)\lt 0$ が成り立つことと同値である。 $f(0)\gt -2$ より $y\gt x^2-2$ が得られ、 $f(-2)\lt 0$ より $y\lt x^2-2x$ が得られる。
(iv) $x \lt -1$ の場合
(1)の範囲と共有点を持つことは、 $f(2)\gt 0$ かつ $f(-2)\lt 0$ が成り立つことと同値である。 $f(2)\gt 0$ より $y\gt x^2+2x$ が得られ、 $f(-2)\lt 0$ より $y\lt x^2-2x$ が得られる。
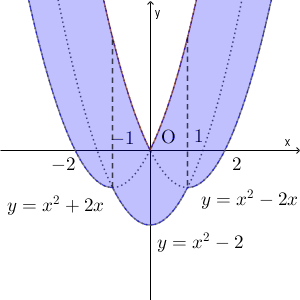
以上より、放物線 $C$ の通りうる範囲は、次の色のついた部分となる(境界線上の点は含まない)。
(終)
解説
$(a,b)$ を動かして放物線がどう動くか、を考えるのは難しいので、 $(x,y)$ を決めたときに、それを満たす放物線があるか、と考えます。(1)を使えば、「 $(x,y)$ を決めたときに、対応する $(a,b)$ が存在するか?」を考えることができるので、これを利用して解くことができます。
放物線を動かして考える場合は、 $x$ を固定してそのときの $y$ のとりうる範囲を考える、という方法もあります。ただ、境界の点が含まれていないため、少し説明が書きづらいです。





