東京大学 理系 2021年度 第2問 解説
問題編
問題
複素数 $a,b,c$ に対して整式 $f(z)=az^2+bz+c$ を考える。 $i$ を虚数単位とする。
(1) $\alpha$, $\beta$, $\gamma$ を複素数とする。 $f(0)=\alpha$, $f(1)=\beta$, $f(i)=\gamma$ が成り立つとき、 $a,b,c$ をそれぞれ $\alpha,\beta,\gamma$ で表せ。
(2) $f(0)$, $f(1)$, $f(i)$ がいずれも $1$ 以上 $2$ 以下の実数であるとき、 $f(2)$ のとりうる範囲を複素数平面上に図示せよ。
考え方
(1)は計算するだけです。(2)は見た目は複素数平面の問題ですが、ベクトルのように考えたほうがわかりやすいかもしれません。
解答編
問題
複素数 $a,b,c$ に対して整式 $f(z)=az^2+bz+c$ を考える。 $i$ を虚数単位とする。
(1) $\alpha$, $\beta$, $\gamma$ を複素数とする。 $f(0)=\alpha$, $f(1)=\beta$, $f(i)=\gamma$ が成り立つとき、 $a,b,c$ をそれぞれ $\alpha,\beta,\gamma$ で表せ。
解答例
(1)
$f(0)=\alpha$ より、 $c=\alpha$ が成り立つ。
$f(1)=\beta$ より、\[ a+b+c=\beta \]が成り立ち、 $f(i)=\gamma$ より\[ -a+bi+c=\gamma \]が成り立つ。辺々を加えると
\begin{eqnarray}
(1+i)b &=& -2\alpha+\beta+\gamma \\[5pt]
b &=& (-2\alpha+\beta+\gamma)\cdot\frac{1-i}{2} \\[5pt]
&=& (-1+i)\alpha+\frac{1-i}{2}\beta+\frac{1-i}{2}\gamma
\end{eqnarray}が得られる。これより
\begin{eqnarray}
a
&=&
\beta-b-c \\[5pt]
&=&
\beta-(-1+i)\alpha-\frac{1-i}{2}\beta-\frac{1-i}{2}\gamma)-\alpha \\[5pt]
&=&
-i\alpha+\frac{1+i}{2}\beta+\frac{-1+i}{2}\gamma \\[5pt]
\end{eqnarray}が得られる。
以上から
\begin{eqnarray}
a &=& -i\alpha+\frac{1+i}{2}\beta+\frac{-1+i}{2}\gamma \\[5pt]
b &=& (-1+i)\alpha+\frac{1-i}{2}\beta+\frac{1-i}{2}\gamma \\[5pt]
c &=& \alpha
\end{eqnarray}と表すことができる。
(終)
解答編 続き
問題
(2) $f(0)$, $f(1)$, $f(i)$ がいずれも $1$ 以上 $2$ 以下の実数であるとき、 $f(2)$ のとりうる範囲を複素数平面上に図示せよ。
解答例
$f(0)=\alpha'+1$, $f(1)=\beta'+1$, $f(i)=\gamma'+1$ とおいて、 $\alpha',\beta',\gamma'$ が $0$ 以上 $1$ 以下の実数を動く場合を考える。
\begin{eqnarray} f(2) &=& 4a+2b+c \\[5pt] &=& 4\left(-i\alpha+\frac{1+i}{2}\beta+\frac{-1+i}{2}\gamma\right) \\ & & +2\left\{(-1+i)\alpha+\frac{1-i}{2}\beta+\frac{1-i}{2}\gamma\right\} +\alpha \\[5pt] &=& -4i\alpha+(2+2i)\beta+(-2+2i)\gamma \\ & & +(-2+2i)\alpha+(1-i)\beta+(1-i)\gamma +\alpha \\[5pt] &=& (-1-2i)\alpha+(3+i)\beta+(-1+i)\gamma \\[5pt] &=& (-1-2i)+(3+i)+(-1+i)\\ & & +(-1-2i)\alpha'+(3+i)\beta'+(-1+i)\gamma' \\[5pt] &=& 1+(-1-2i)\alpha'+(3+i)\beta'+(-1+i)\gamma' \\[5pt] \end{eqnarray}となる。$\alpha'$ が $0\leqq \alpha'\leqq 1$ を満たしながら動くとき、点 $\left( 1+(-1-2i)\alpha' \right)$ の動く範囲の全体は次の線分となる(両端を含む)。

さらに、 $\beta'$ も $0\leqq \beta'\leqq 1$ を満たしながら動くとき、点 $\left( 1+(-1-2i)\alpha'+(3+i)\beta' \right)$ の動く範囲の全体は次の四角形となる(境界線上の点を含む)。

また、点 $\left( 1+(-1-2i)\alpha'+(3+i)\beta'+(-1+i)\gamma' \right)$ の動く範囲の全体は、 $\gamma'=0$ のときは先ほどの図のようになり、 $\gamma'=1$ のときは次の通りとなる(境界線上の点も含む)。

$\gamma'$ が $0\leqq \gamma'\leqq 1$ を満たしながら動くとき、この2つの図形を、原点と点 $(-1+i)$ とを結んだ線分に平行に移動するので、 $f(2)$ のとりうる範囲は次の通りとなる(境界線上の点を含む)。
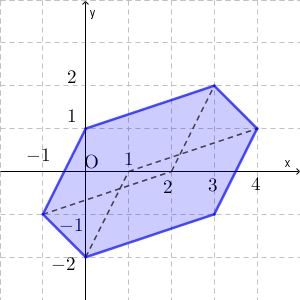
(終)





