東京大学 理系 2020年度 第3問 解説
問題編
問題
$-1\leqq t\leqq 1$ を満たす実数 $t$ に対して、
\begin{eqnarray} x(t) &=& (1+t)\sqrt{1+t} \\[5pt] y(t) &=& 3(1+t)\sqrt{1-t} \\[5pt] \end{eqnarray}とする。座標平面上の点 $\mathrm{P}(x(t),y(t))$ を考える。(1) $-1\lt t\leqq 1$ における $t$ の関数 $\dfrac{y(t)}{x(t)}$ は単調に減少することを示せ。
(2) 原点と P の距離を $f(t)$ とする。 $-1\leqq t\leqq 1$ における $t$ の関数 $f(t)$ の増減を調べ、最大値を求めよ。
(3) $t$ が $-1\leqq t \leqq 1$ を動くときの P の軌跡を $C$ とし、 $C$ と $x$ 軸で囲まれた領域を $D$ とする。原点を中心として $D$ を時計回りに $90^{\circ}$ 回転させるとき、 $D$ が通過する領域の面積を求めよ。
考え方
(1)は微分するまでもないですが、微分して示してもいいです。
(2)は、 $\{f(t)\}^2$ を計算すればいいですね。計算はそれほど大変ではありません。
(3)は、まず図形をかいてみます。サイクロイドのような図形になりますが、 $y(t)$ の式にある $3$ のせいで、少し縦長になります。そのため、通過する領域に少し注意が必要です。ただ、このことは(2)の結果を使えばすぐにわかりますね。誘導が親切です。
どの小問も、油断すると計算が大変になってしまいます。簡略化できないか考えつつ、計算していくようにしましょう。
解答編
問題
$-1\leqq t\leqq 1$ を満たす実数 $t$ に対して、
\begin{eqnarray} x(t) &=& (1+t)\sqrt{1+t} \\[5pt] y(t) &=& 3(1+t)\sqrt{1-t} \\[5pt] \end{eqnarray}とする。座標平面上の点 $\mathrm{P}(x(t),y(t))$ を考える。(1) $-1\lt t\leqq 1$ における $t$ の関数 $\dfrac{y(t)}{x(t)}$ は単調に減少することを示せ。
解答
(1)
\begin{eqnarray}
\frac{y(t)}{x(t)}
&=&
\dfrac{3(1+t)\sqrt{1-t} }{(1+t)\sqrt{1+t} } \\[5pt]
&=&
3\sqrt{\dfrac{2}{1+t}-1} \\[5pt]
\end{eqnarray}なので、 $-1\lt t\leqq 1$ において、 $\dfrac{y(t)}{x(t)}$ は単調に減少する。
(終)
解答編 つづき
問題
(2) 原点と P の距離を $f(t)$ とする。 $-1\leqq t\leqq 1$ における $t$ の関数 $f(t)$ の増減を調べ、最大値を求めよ。
解答
\begin{eqnarray} \{f(t)\}^2 &=& \{x(t)\}^2+\{y(t)\}^2 \\[5pt] &=& (1+t)^3+9(1+t)^2(1-t) \\[5pt] &=& (1+t)^2\{(1+t)+9(1-t)\} \\[5pt] &=& (1+t)^2(10-8t) \\[5pt] \end{eqnarray}であり、これを微分すると \begin{eqnarray} & & 2(1+t)(10-8t)+(1+t)^2\cdot(-8) \\[5pt] &=& (1+t)\{2(10-8t)-8(1+t) \} \\[5pt] &=& (1+t)(12-24t) \\[5pt] \end{eqnarray}となる。よって、 $\{f(t)\}^2$ は $-1\leqq t\leqq \dfrac{1}{2}$ の範囲で単調増加、 $\dfrac{1}{2}\leqq t\leqq 1$ の範囲で単調減少となる。 $f(t)$ は0以上の値なので、 $f(t)$ と $\{f(t)\}^2$ は単調増加・単調減少となる範囲がそれぞれ一致するため、 $f(t)$ も $-1\leqq t\leqq \dfrac{1}{2}$ の範囲で単調増加、 $\dfrac{1}{2}\leqq t\leqq 1$ の範囲で単調減少となる。
これより最大となるのは $t=\dfrac{1}{2}$ のときであり、そのときの $f(t)$ の値は
\begin{eqnarray}
& &
\sqrt{ \left(1+\frac{1}{2}\right)^2 \left(10-8\cdot\frac{1}{2}\right) } \\[5pt]
&=&
\sqrt{ \dfrac{9}{4} \cdot 6 } \\[5pt]
&=&
\frac{3\sqrt{6} }{2} \\[5pt]
\end{eqnarray}である。
(終)
解答編 つづき
問題
(3) $t$ が $-1\leqq t \leqq 1$ を動くときの P の軌跡を $C$ とし、 $C$ と $x$ 軸で囲まれた領域を $D$ とする。原点を中心として $D$ を時計回りに $90^{\circ}$ 回転させるとき、 $D$ が通過する領域の面積を求めよ。
解答
(3)
$x(t)=(1+t)^{\frac{3}{2} }$ なので、 $t$ について単調増加である。また、(1)より OP の傾きは単調に減少し、 $\lim_{t\to -1+0}\dfrac{y(t)}{x(t)}=\infty$ である。また、(2)より、線分 OP は $t=\dfrac{1}{2}$ のときに最大値 $\dfrac{3\sqrt{6} }{2}$ をとることから、領域 $D$ は以下の色のついた部分となる。
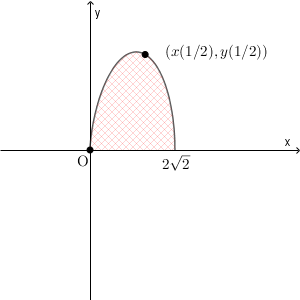
これを時計回りに $90^{\circ}$ 回転させたときに通過する領域は、次の色のついた部分である。
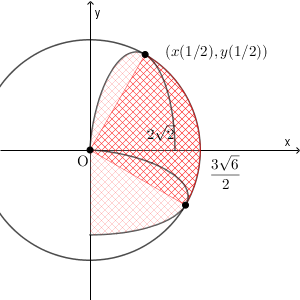
この領域の面積は、 $D$ の面積と、半径が $\dfrac{3\sqrt{6} }{2}$ で中心角が $90^{\circ}$ のおうぎ形の面積の和である。
$D$ の面積は
\begin{eqnarray}
& &
\int_{0}^{2\sqrt{2} } y dx \\[5pt]
&=&
\int_{-1}^{1} y(t) \dfrac{dx(t)}{dt} dt \\[5pt]
&=&
\int_{-1}^{1} 3(1+t)\sqrt{1-t} \cdot \frac{3}{2}\sqrt{1+t} dt \\[5pt]
&=&
\frac{9}{2} \int_{-1}^{1} (1+t)\sqrt{1-t^2} dt \\[5pt]
\end{eqnarray}である。ここで、 $t\sqrt{1-t^2}$ は奇関数なので、\[ \int_{-1}^{1} t\sqrt{1-t^2} dt = 0\]である。また、\[ \int_{-1}^{1} \sqrt{1-t^2} dt \]は半径が $1$ の半円の面積なので、 $\dfrac{\pi} {2}$ である。よって、 $D$ の面積は\[ \frac{9}{2}\cdot\frac{\pi}{2}=\frac{9}{4}\pi \]となる。
また、おうぎ形の面積は\[ \frac{3\sqrt{6} }{2}\cdot \frac{3\sqrt{6} }{2}\cdot \pi\cdot\frac{1}{4}=\frac{27}{8}\pi \]なので、 $D$ が通過する領域の面積は\[ \frac{9}{4}\pi+\frac{27}{8}\pi=\frac{45}{8}\pi \]である。
(終)





