東京大学 理系 2020年度 第2問 解説
問題編
問題
平面上の点 P, Q, R が同一直線上にないとき、それらを3頂点とする三角形の面積を $\triangle \mathrm{PQR} $ で表す。また、 P, Q, R が同一直線上にあるときは、 $\triangle \mathrm{PQR}=0$ とする。
A, B, C を平面上の3点とし、 $\triangle \mathrm{ABC}=1$ とする。この平面上の点 X が\[ 2\leqq \triangle \mathrm{ABX} +\triangle \mathrm{BCX} +\triangle \mathrm{CAX} \leqq 3 \]を満たしながら動くとき、 X の動きうる範囲の面積を求めよ。
考え方
A, B, C がどういう点なのかわからないため、どのように攻めていけばいいか、なかなか方針を立てにくいですね。座標や三角比、ベクトルなどを使い始める前に、まずは図をかいてみましょう。図形の性質を用いれば、かなりスッキリと考えることができます。
解答編
問題
平面上の点 P, Q, R が同一直線上にないとき、それらを3頂点とする三角形の面積を $\triangle \mathrm{PQR} $ で表す。また、 P, Q, R が同一直線上にあるときは、 $\triangle \mathrm{PQR}=0$ とする。
A, B, C を平面上の3点とし、 $\triangle \mathrm{ABC}=1$ とする。この平面上の点 X が\[ 2\leqq \triangle \mathrm{ABX} +\triangle \mathrm{BCX} +\triangle \mathrm{CAX} \leqq 3 \]を満たしながら動くとき、 X の動きうる範囲の面積を求めよ。
解答
X が三角形 ABC の周や内部にあるときは、\[ \triangle \mathrm{ABX} +\triangle \mathrm{BCX} +\triangle \mathrm{CAX}=\triangle \mathrm{ ABC }=1 \]である。よって、 X が三角形 ABC の外部にある場合だけを考えればよい。
三角形の外部の領域を、直線 AB, BC, CA で分け、次のように2つのタイプにわける。

(i) タイプIの場合
まず、直線 AC について、 X と B が反対側にある場合を考える。

このとき、
\begin{eqnarray}
& &
\triangle \mathrm{ABX} +\triangle \mathrm{BCX} +\triangle \mathrm{CAX} \\[5pt]
&=&
\triangle \mathrm{ ABC }+2\triangle \mathrm{ ACX } \\[5pt]
&=&
1+2\triangle \mathrm{ ACX } \\[5pt]
\end{eqnarray}である。
よって、 X が条件を満たすことは、\[ \dfrac{1}{2} \leqq \triangle\mathrm{ ACX } \leqq 1 \]を満たすことと同値である。
AC を底辺と考えれば、上の条件を満たすように X が動くとき、動きうる領域は下の図の色のついた部分(四角形 DEFG)である。

なお、DE, FG は AC に平行で、 $\mathrm{ AD }=\mathrm{ DG }=\dfrac{1}{2}\mathrm{ AB }$, $\mathrm{ CE }=\mathrm{ EF }=\dfrac{1}{2}\mathrm{ BC }$ である。よって、この領域の面積は、\[ 2^2-\left(\dfrac{3}{2}\right)^2=\frac{7}{4} \]となる。同じタイプの他の領域についても同様なので、全部で\[ \frac{7}{4}\cdot 3=\dfrac{21}{4} \]となる。
(ii) タイプIIの場合
まず、直線 AB について、 X と C が同じ側にある場合を考える。
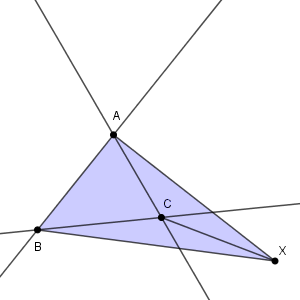
このとき、
\begin{eqnarray}
& &
\triangle \mathrm{ABX} +\triangle \mathrm{BCX} +\triangle \mathrm{CAX} \\[5pt]
&=&
2\triangle \mathrm{ ABX }-1
\end{eqnarray}
である。よって、 X が条件を満たすことは、\[ \dfrac{3}{2} \leqq \triangle \mathrm{ ABX } \leqq 2 \]を満たすことと同値である。
AB を底辺と考えれば、上の条件を満たすように X が動くとき、動きうる領域は下の図の色のついた部分(四角形 DEFG)である。

なお、DE, FG は AB に平行で、 $\mathrm{ CD }=\mathrm{ DG }=\dfrac{1}{2}\mathrm{ BC }$, $\mathrm{ CE }=\mathrm{ EF }=\dfrac{1}{2}\mathrm{ AC }$ である。よって、この領域の面積は、\[ 1^2-\left(\dfrac{1}{2}\right)^2=\frac{3}{4} \]となる。同じタイプの他の領域についても同様なので、全部で\[ \frac{3}{4}\cdot 3=\dfrac{9}{4} \]となる。
(i)(ii)より、求める面積は $\dfrac{21}{4}+\dfrac{9}{4}=\dfrac{15}{2}$ となる。
(終)





