東京大学 理系 2020年度 第5問 解説
問題編
問題
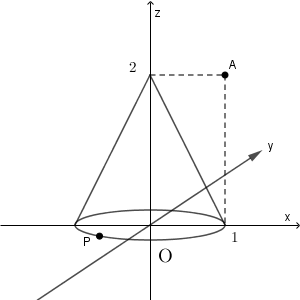
座標空間において、 $xy$ 平面上の原点を中心とする半径 $1$ の円を考える。この円を底面とし、点 $(0,0,2)$ を頂点とする円錐(内部を含む)を $S$ とする。また、点 $\mathrm{A}(1,0,2)$ を考える。
(1) 点 $\mathrm{P}$ が $S$ の底面を動くとき、線分 $\mathrm{AP}$ が通過する部分を $T$ とする。平面 $z=1$ による $S$ の切り口および、平面 $z=1$ による $T$ の切り口を同一平面上に図示せよ。
(2) 点 $\mathrm{P}$ が $S$ を動くとき、線分 $\mathrm{AP}$ が通過する部分の体積を求めよ。
考え方
円錐自体はわかりやすく、切り口も想像しやすいです。(1)で断面を考えるので、(2)はそのまま断面がどうなるかを考えて積分すればいいだろうと予想できます。
(1)の答えが(2)を考えるヒントになっています。 $S$ の断面は、点 P が $S$ を平面 $z=1$ で切ったときの断面を動くときで、 $T$ の断面は点 P が $S$ の底面を動くときに対応します。これは、点 P の $z$ 座標が動くにつれて、断面は横にスライドしていく、ということを表しています。これから答えの予想ができるので、これをヒントにして他の平面で切ったときの断面図も考えましょう。
解答編
問題
座標空間において、 $xy$ 平面上の原点を中心とする半径 $1$ の円を考える。この円を底面とし、点 $(0,0,2)$ を頂点とする円錐(内部を含む)を $S$ とする。また、点 $\mathrm{A}(1,0,2)$ を考える。
(1) 点 $\mathrm{P}$ が $S$ の底面を動くとき、線分 $\mathrm{AP}$ が通過する部分を $T$ とする。平面 $z=1$ による $S$ の切り口および、平面 $z=1$ による $T$ の切り口を同一平面上に図示せよ。
解答
(1)
平面 $z=1$ による $S$ の切り口は $(0,0,1)$ を中心とする半径 $\dfrac{1}{2}$ の円である。
次に、 $T$ の切り口を考える。まず、点 $\mathrm{P}$ が $S$ の底面の周を動く場合を考える。このとき、点 $\mathrm{P}$ の座標は、 $(\cos\theta,\sin\theta,0)$ とかける( $0\leqq \theta\lt 2\pi$ )。線分 $\mathrm{AP}$ と平面 $z=1$ との共有点を $\mathrm{M}$ とおくと、
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ OM } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OA } }+\dfrac{1}{2}\overrightarrow{ \mathrm{ AP } } \\[5pt]
&=&
(1,0,2)+\dfrac{1}{2}\left( \cos\theta-1,\sin\theta,-2 \right) \\[5pt]
&=&
\left( \frac{1}{2}+\frac{1}{2}\cos\theta,\frac{1}{2}\sin\theta,1 \right) \\[5pt]
\end{eqnarray}となる。よって、 $\theta$ が動くと、この軌跡は、平面 $z=1$ 上で、中心 $\left(\dfrac{1}{2}, 0, 1\right)$ を中心とした半径 $\dfrac{1}{2}$ の円となる。点 $P$ が $S$ の底面の内部も動くと、点 M はこの円の内部を動く。
以上より、 $S,T$ の切り口は以下のようになる。
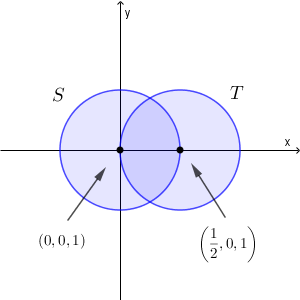
(終)
解答編 つづき
問題
(2) 点 $\mathrm{P}$ が $S$ を動くとき、線分 $\mathrm{AP}$ が通過する部分の体積を求めよ。
解答
線分 AP が通過する部分からなる立体を $V$ とおく。 $V$ を平面 $z=t$ $( 0\leqq t \leqq 2 )$ で切ったときの断面について考える。
まず、円錐 $S$ を平面 $z=c$ $(0\leqq c\leqq t)$ で切り、点 P がこの切り口の周を動く場合を考える。

このときの切り口は円周であり、円の半径は $1-\dfrac{c}{2}$ である。よって、点 P の座標は\[ \left(\left(1-\dfrac{c}{2}\right)\cos\theta, \left(1-\dfrac{c}{2}\right)\sin\theta, c\right) \]とかける( $0\leqq \theta\lt 2\pi$ )。線分 AP と平面 $z=t$ との共有点を M とすると、\[ \overrightarrow{ \mathrm{ AM } }=\dfrac{2-t}{2-c}\overrightarrow{ \mathrm{ AP } } \]なので
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ AM } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OA } }+ \dfrac{2-t}{2-c}\overrightarrow{ \mathrm{ AP } } \\[5pt]
&=&
(1,0,2)+ \dfrac{2-t}{2-c} \left(\left(1-\dfrac{c}{2}\right)\cos\theta -1, \left(1-\dfrac{c}{2}\right)\sin\theta, c-2 \right) \\[5pt]
&=&
\left(\left(\dfrac{2-t}{2}\right)\cos\theta -\dfrac{2-t}{2-c}+1, \left(\dfrac{2-t}{2}\right)\sin\theta, t \right) \\[5pt]
\end{eqnarray}と表すことができる。よって、点 M は、平面 $z=t$ 上で、中心が $\left(-\dfrac{2-t}{2-c}+1,0,t\right)$ で半径が $\dfrac{2-t}{2}$ の円の円周を動く。点 P が円の内部も動く場合は、点 M もこの円の内部を動く。
点 P が $0\leqq c\leqq t$ の範囲を動くとき、 $-\dfrac{2-t}{2-c}+1$ は $-\dfrac{2-t}{2-t}+1=0$ 以上\[-\dfrac{2-t}{2-0}+1=\frac{t}{2}\]以下の値をすべてとる。よって、点 P が円錐 $S$ の $z\leqq t$ の範囲を動くとき、立体 $V$ の平面 $z=t$ での断面は、半径が $\dfrac{2-t}{2}$ の円(内部も含む)で、中心が $(0,0,t)$ から $\left(\dfrac{t}{2},0,t\right)$ まで移動したときの軌跡となるので、次のようになる。
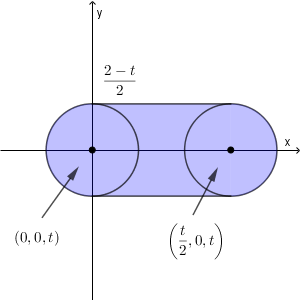
よって、断面積は、長方形と円に分けて、\[ (2-t)\times \frac{t}{2} +\pi\left(\dfrac{2-t}{2}\right)^2 \]となる。よって、線分 AP が通過する部分の体積は
\begin{eqnarray}
& &
\int_0^2 \left\{(2-t)\times \frac{t}{2} +\pi\left(\dfrac{2-t}{2}\right)^2 \right\} dt \\[5pt]
&=&
\int_0^2 \left( \frac{2t-t^2}{2} +\pi\dfrac{(t-2)^2}{4} \right ) dt \\[5pt]
&=&
\left[\frac{1}{2}t^2-\frac{t^3}{6} +\pi\frac{(t-2)^3}{12}\right]_0^2 \\[5pt]
&=&
2-\frac{4}{3} +\frac{2}{3}\pi \\[5pt]
&=&
\frac{2}{3} +\frac{2}{3}\pi \\[5pt]
\end{eqnarray}と求められる。
(終)





