東京大学 理系 2018年度 第5問 解説
問題編
問題
複素数平面上の原点を中心とする半径 $1$ の円を C とする。点 $\mathrm{ P }(z)$ は C 上にあり、点 $\mathrm{ A }(1)$ とは異なるとする。点 P における円 C の接線に関して、点 A と対称な点を $\mathrm{ Q }(u)$ とする。 $w=\dfrac{1}{1-u}$ とおき、 w と共役な複素数を $\overline{w}$ で表す。
(1) u と $\dfrac{\overline{w} }{w}$ を z についての整式として表し、絶対値の商 $\dfrac{|w+\overline{w}-1|}{|w|}$ を求めよ。
(2) C のうち実部が $\dfrac{1}{2}$ 以下の複素数で表される部分を $C'$ とする。点 $\mathrm{ P }(z)$ が $C'$ 上を動くときの点 $\mathrm{ R }(w)$ の軌跡を求めよ。
考え方
(1)の u の部分ができれば、後はなんとかなるかもしれませんが、一番初めの u がやっかいです。計算だけで進めていくのは厳しいです。図形の性質を使って考えましょう。
(2)は、(1)を使えば、「求める軌跡がどんな図形の一部なのか」がわかります。あとは、その図形のどの部分かを考えますが、また視点を変えて攻めていく必要があります。
解答編
問題
複素数平面上の原点を中心とする半径 $1$ の円を C とする。点 $\mathrm{ P }(z)$ は C 上にあり、点 $\mathrm{ A }(1)$ とは異なるとする。点 P における円 C の接線に関して、点 A と対称な点を $\mathrm{ Q }(u)$ とする。 $w=\dfrac{1}{1-u}$ とおき、 w と共役な複素数を $\overline{w}$ で表す。
(1) u と $\dfrac{\overline{w} }{w}$ を z についての整式として表し、絶対値の商 $\dfrac{|w+\overline{w}-1|}{|w|}$ を求めよ。
(2) C のうち実部が $\dfrac{1}{2}$ 以下の複素数で表される部分を $C'$ とする。点 $\mathrm{ P }(z)$ が $C'$ 上を動くときの点 $\mathrm{ R }(w)$ の軌跡を求めよ。
解答
(1)
AQ の中点を H とする。また、 $\angle \mathrm{ AOP }=\theta$ とする。
(i) $0\lt \theta \lt \pi$ のとき
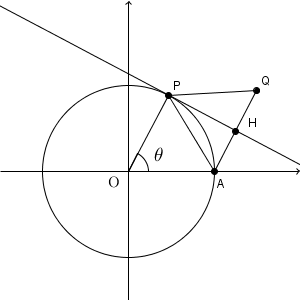
接弦定理と円周角の定理より、 $\angle \mathrm{ APH }=\dfrac{\theta}{2}$ なので、 $\angle \mathrm{ APQ }=\theta$ となる。よって、点 Q は、点 P を中心として、点 A を反時計回りに $\theta$ だけ回転した点だから
\begin{eqnarray}
u
&=&
(1-z)z+z \\[5pt]
&=&
-z^2+2z \\[5pt]
\end{eqnarray}となる。
(ii) $\theta=\pi$ のとき
$\mathrm{ P }(-1)$, $\mathrm{ Q }(-3)$ なので、このときも\[ u=-z^2+2z \]が成り立つ。
(iii) $\pi\lt \theta \lt 2\pi$ のとき
実軸に関して対称移動すると、(i)の状況になるので\[ \overline{u}=-\overline{z}^2+2\overline{z} \]が成り立つ。両辺の共役複素数を考えると、このときも\[ u=-z^2+2z \]が成り立つ。
(i)(ii)(iii)から、\[ u=-z^2+2z \]となる。
\begin{eqnarray} w &=& \frac{1}{1-u} \\[5pt] &=& \frac{1}{1-(-z^2+2z)} \\[5pt] &=& \frac{1}{z^2-2z+1} \\[5pt] \end{eqnarray}である。また、 $z\overline{z}=1$ だから、 \begin{eqnarray} \overline{w} &=& \frac{1}{\overline{z}^2-2\overline{z}+1} \\[5pt] &=& \frac{z^2}{1-2z+z^2} \\[5pt] \end{eqnarray}となる。よって、 \begin{eqnarray} & & \frac{\overline{w} }{w} \\[5pt] &=& \frac{z^2}{1-2z+z^2}\times (z^2-2z+1) \\[5pt] &=& z^2 \end{eqnarray}となる。また、
\begin{eqnarray}
& &
\frac{|w+\overline{w}-1|}{|w|} \\[5pt]
&=&
|1+\frac{\overline{w} }{w}-\frac{1}{w}| \\[5pt]
&=&
|1+z^2-(z^2-2z+1)| \\[5pt]
&=&
2|z| \\[5pt]
&=&
2
\end{eqnarray}となる。
以上より、
\begin{eqnarray}
u &=& -z^2+2z \\[5pt]
\frac{\overline{w} }{w} &=& z^2 \\[5pt]
\frac{|w+\overline{w}-1|}{|w|} &=& 2 \\[5pt]
\end{eqnarray}となる。
(2)
$w=x+yi$ とする(x, y は実数)。
(1)より
\begin{eqnarray}
|2x-1| &=& 2\sqrt{x^2+y^2} \\[5pt]
4x^2-4x+1 &=& 4(x^2+y^2) \\[5pt]
x &=& -y^2+\frac{1}{4} \\[5pt]
\end{eqnarray}が成り立つ。よって、求める軌跡は、 $x = -y^2+\dfrac{1}{4}$ の一部である。
(1)で求めた通り\[ w=\frac{1}{z^2-2z+1}=\frac{1}{(z-1)^2} \]が成り立つ。ここで、 P が $C'$ 上を動くとき、 $(z-1)^2$ の偏角が取りうる値を求める。
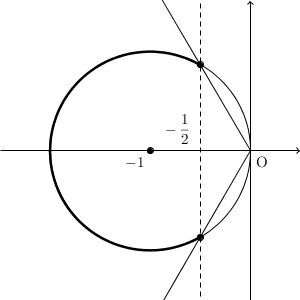
上の図の太線が、 $z-1$ の動く範囲である。図より、 P が $C'$ 上を動くとき、 $z-1$ の偏角は、 $\dfrac{2}{3}\pi$ 以上 $\dfrac{4}{3}\pi$ 以下のすべての値をとる。よって、 $(z-1)^2$ の偏角は、 $\dfrac{4}{3}\pi$ 以上 $\dfrac{8}{3}\pi$ 以下のすべての値をとる。
$w=\dfrac{1}{(z-1)^2}$ なので、 $w$ の偏角は、 $-\dfrac{8}{3}\pi$ 以上 $-\dfrac{4}{3}\pi$ 以下のすべての値をとる。これより、 $-\dfrac{2}{3}\pi$ 以上 $\dfrac{2}{3}\pi$ 以下のすべての値をとることがわかる。
$x = -y^2+\dfrac{1}{4}$ と、 $y=\sqrt{3}x$, $y=-\sqrt{3}x$ との交点は、それぞれ $\left(-\dfrac{1}{2},\dfrac{\sqrt{3} }{2}\right)$, $\left(-\dfrac{1}{2},-\dfrac{\sqrt{3} }{2}\right)$ となる。
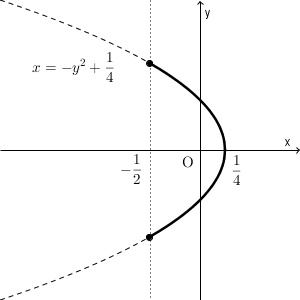
以上より、 $\mathrm{ R } (w)$ の軌跡は、 $w=x+yi$ としたとき、 $x = -y^2+\dfrac{1}{4}$ の $x\geqq -\dfrac{1}{2}$ を満たす部分となる。





