東京大学 理系 2018年度 第6問 解説

問題編

問題

　座標空間内の4点 $\mathrm{ O }(0,0,0)$, $\mathrm{ A }(1,0,0)$, $\mathrm{ B }(1,1,0)$, $\mathrm{ C }(1,1,1)$ を考える。

　$\dfrac{1}{2}\lt r \lt 1$ とする。点 P が線分 OA, AB, BC 上を動くときに点 P を中心とする半径 r の球（内部を含む）が通過する部分を、それぞれ $V_1$, $V_2$, $V_3$ とする。

(1) 平面 $y=t$ が $V_1$, $V_3$ 双方と共有点をもつような t の範囲を与えよ。さらに、この範囲の t に対し、平面 $y=t$ と $V_1$ の共通部分および、平面 $y=t$ と $V_3$ の共通部分を同一平面上に図示せよ。

(2) $V_1$ と $V_3$ の共通部分が $V_2$ に含まれるための r についての条件を求めよ。

(3) r は(2)の条件をみたすとする。 $V_1$ の体積を S とし、 $V_1$ と $V_2$ の共通部分の体積を T とする。 $V_1$, $V_2$, $V_3$ を合わせて得られる立体 V の体積を S と T を用いて表せ。

(4) ひきつづき r は(2)の条件をみたすとする。 S と T を求め、 V の体積を決定せよ。

考え方

断面で切ったときの図形で考えていきましょう。「球が通過する部分に含まれる点」と「中心が移動する線分」との距離について考えると、範囲が考えやすいかもしれません。

(3)は、(2)から、3つの図形の共通部分について何が言えるかを考えましょう。

(4)は、ここまでができていれば、たいして難しくはない積分です。ここにたどりつくまでが難しいです。

---

解答編

問題

　座標空間内の4点 $\mathrm{ O }(0,0,0)$, $\mathrm{ A }(1,0,0)$, $\mathrm{ B }(1,1,0)$, $\mathrm{ C }(1,1,1)$ を考える。

　$\dfrac{1}{2}\lt r \lt 1$ とする。点 P が線分 OA, AB, BC 上を動くときに点 P を中心とする半径 r の球（内部を含む）が通過する部分を、それぞれ $V_1$, $V_2$, $V_3$ とする。

(1) 平面 $y=t$ が $V_1$, $V_3$ 双方と共有点をもつような t の範囲を与えよ。さらに、この範囲の t に対し、平面 $y=t$ と $V_1$ の共通部分および、平面 $y=t$ と $V_3$ の共通部分を同一平面上に図示せよ。

解答

(1)
まず、平面 $y=t$ と $V_1$ の共通部分について考える。

$0\leqq x\leqq 1$ のとき、平面 $y=t$ 上の点 $(x,t,z)$ について考える。この点に一番近い線分 OA 上の点は $(x,0,0)$ なので、この2点間の距離が r 以下なら、点 $(x,t,z)$ は $V_1$ 内にあるといえる。また、 r より大きければ、 $V_1$ 内にはない。よって、このとき、平面 $y=t$ と $V_1$ との共通部分は
\begin{eqnarray} t^2+z^2 & \leqq & r^2 \\[5pt] z^2 & \leqq & r^2-t^2 \\[5pt] \end{eqnarray}である。

$x\lt 0$ のときは、平面 $y=t$ 上の点 $(x,t,z)$ が $V_1$ に含まれるのは、この点と線分 OA に一番近い点との距離が $r$ 以下、つまり、 $(0,0,0)$ との距離が $r$ 以下のときに限る。よって、このとき、平面 $y=t$ と $V_1$ との共通部分は
\begin{eqnarray} x^2+t^2+z^2 & \leqq & r^2 \\[5pt] x^2+z^2 & \leqq & r^2-t^2 \\[5pt] \end{eqnarray}である。

$x\gt 1$ のときは、平面 $y=t$ 上の点 $(x,t,z)$ が $V_1$ に含まれるのは、この点と $(1,0,0)$ との距離が $r$ 以下のときに限る。よって、このとき、平面 $y=t$ と $V_1$ との共通部分は
\begin{eqnarray} (x-1)^2+t^2+z^2 & \leqq & r^2 \\[5pt] (x-1)^2+z^2 & \leqq & r^2-t^2 \\[5pt] \end{eqnarray}である。

以上から、平面 $y=t$ と $V_1$ との共通部分が存在するのは $r^2-t^2\geqq 0$ のとき、つまり、 $-r\leqq t \leqq r$ のときで、共通部分は、次の図の色のついた部分となる（境界線上の点を含む）。

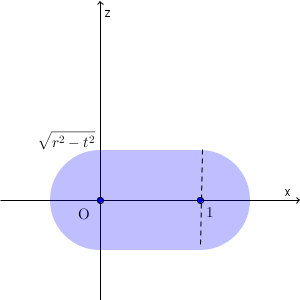
次に、平面 $y=t$ と $V_3$ の共通部分について考える。

$0\leqq z\leqq 1$ のとき、平面 $y=t$ 上の点 $(x,t,z)$ について考える。この点に一番近い線分 BC 上の点は $(1,1,z)$ なので、平面 $y=t$ 上の点 $(x,t,z)$ が $V_3$ に含まれるのは、点 $(x,t,z)$ と $(1,1,z)$ との距離が $r$ 以下のときに限る。よって、このとき、平面 $y=t$ と $V_3$ との共通部分は
\begin{eqnarray} (x-1)^2+(t-1)^2 & \leqq & r^2 \\[5pt] (x-1)^2 & \leqq & r^2-(t-1)^2 \\[5pt] \end{eqnarray}である。

$z\lt 0$ のときは、平面 $y=t$ 上の点 $(x,t,z)$ が $V_3$ に含まれるのは、この点と線分 BC に一番近い点との距離が $r$ 以下、つまり $(1,1,0)$ との距離が $r$ 以下のときに限る。よって、このとき、平面 $y=t$ と $V_3$ との共通部分は
\begin{eqnarray} (x-1)^2+(t-1)^2+z^2 & \leqq & r^2 \\[5pt] (x-1)^2+z^2 & \leqq & r^2-(t-1)^2 \\[5pt] \end{eqnarray}である。

$z\gt 1$ のときは、平面 $y=t$ 上の点 $(x,t,z)$ が $V_3$ に含まれるのは、この点と $(1,1,1)$ との距離が $r$ 以下のときに限る。よって、このとき、平面 $y=t$ と $V_3$ との共通部分は
\begin{eqnarray} (x-1)^2+(t-1)^2+(z-1)^2 & \leqq & r^2 \\[5pt] (x-1)^2+(z-1)^2 & \leqq & r^2-(t-1)^2 \\[5pt] \end{eqnarray}である。

以上から、平面 $y=t$ と $V_3$ との共通部分が存在するのは
\begin{eqnarray} r^2-(1-t)^2\geqq 0 \\[5pt] (t-1)^2\leqq r^2 \\[5pt] -r\leqq t-1 \leqq r \\[5pt] 1-r\leqq t \leqq 1+r \\[5pt] \end{eqnarray}のときであり、共通部分は、次の図の色のついた部分となる（境界線上の点を含む）。

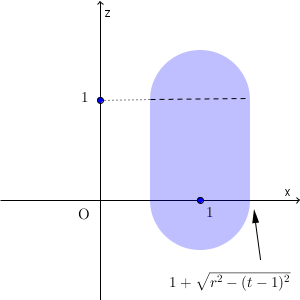
これらと $\dfrac{1}{2}\lt r \lt 1$ から、平面 $y=t$ が $V_1,V_3$ の双方と共有点をもつ t の範囲は、\[ 1-r\leqq t \leqq r \]である。また、 $(1,t,0)$ を中心とした半円の半径の2乗は、それぞれ $r^2-t^2$、 $r^2-(1-t)^2$ であり、これが等しくなるのは $t=\dfrac{1}{2}$ である。これより小さくなれば、 $V_1$ との共有部分の方が大きくなり、これより大きくなれば、 $V_3$ との共有部分の方が大きくなる。

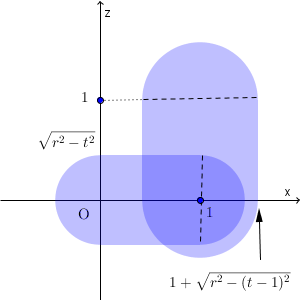
よって、 $1-r \leqq t \lt \dfrac{1}{2}$ のときの共通部分は、次の図の色のついた部分となる（境界線上の点を含む）。

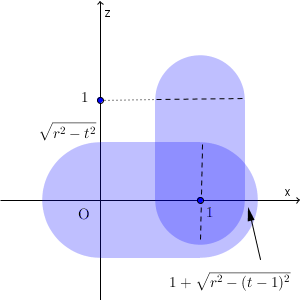
$t=\dfrac{1}{2}$ のときの共通部分は、次の図の色のついた部分となる（境界線上の点を含む）。

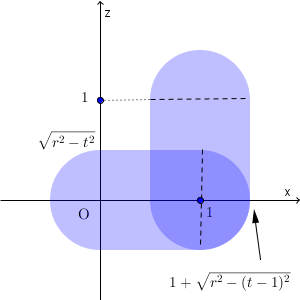
$\dfrac{1}{2} \lt t \leqq 1+r$ のときの共通部分は、次の図の色のついた部分となる（境界線上の点を含む）。

解答編 つづき

問題

(2) $V_1$ と $V_3$ の共通部分が $V_2$ に含まれるための r についての条件を求めよ。

解答

(1)より、 $V_1$ と $V_3$ の共通部分が存在する\[ 1-r\leqq t \leqq r \]の範囲で考える。このとき、\[ 0\lt 1-r\lt r \lt 1 \]より、 $V_1$ と $V_3$ の共通部分内の点 $(x,y,z)$ に一番近い線分 AB 上の点は $(1,y,0)$ である。よって、 $V_1$ と $V_3$ の共通部分が $V_2$ に含まれるのは、平面 $y=t$ で共通部分を切った断面が、つねに $(x,z)=(1,0)$ を中心とした半径 r の円内に含まれるときである。

(1)より、平面 $y=t$ で共通部分を切った断面が、 $(x,z)=(1,0)$ から一番離れている点は $(1-\sqrt{r^2-(t-1)^2},\sqrt{r^2-t^2})$ なので、この2点間の距離が r 以下となるのは
\begin{eqnarray} \{ r^2-(t-1)^2 \} +(r^2-t^2) \leqq r^2 \\[5pt] 2r^2-2t^2+2t-1 \leqq r^2 \\[5pt] r^2 \leqq 2t^2-2t+1 \\[5pt] r^2 \leqq 2 \left(t-\frac{1}{2}\right)^2 +\frac{1}{2} \\[5pt] \end{eqnarray}が成り立つときである。右辺は $t=\dfrac{1}{2}$ のときに最小となるが、今考えている t の範囲は $1-r\leqq t \leqq r$ なので、実際に $t=\dfrac{1}{2}$ の値を取りうる。よって、 r は\[ -\frac{\sqrt{2} }{2}\leqq r \leqq \frac{\sqrt{2} }{2} \]となる。

もともと、 $\dfrac{1}{2}\lt r \lt 1$ なので、求める条件は\[ \frac{1}{2}\lt r \leqq \frac{\sqrt{2} }{2} \]となる。

解答編 つづき

問題

(3) r は(2)の条件をみたすとする。 $V_1$ の体積を S とし、 $V_1$ と $V_2$ の共通部分の体積を T とする。 $V_1$, $V_2$, $V_3$ を合わせて得られる立体 V の体積を S と T を用いて表せ。

解答

(3)
$V_1$, $V_2$, $V_3$ は、半径 r の球をある直線に沿って $1$ だけ動かしたときに通過する部分なので、合同である。よって、3つとも、体積は等しい。

また、 $V_3$ を、直線 $x-1=z=0$ について回転し、 $(1,1,1)$ が $(0,1,0)$ にくるようにする。すると、 $V_1$ と $V_2$ を合わせた図形と, $ V_2$ と $V_3$ を合わせた図形は、平面 $y=\dfrac{1}{2}$ について対称なので、 $V_1$ と $V_2$ の共通部分、 $V_2$ と $V_3$ の共通部分は合同であり、体積は等しい。

$V_1$ と $V_3$ の共通部分の体積を U とする。今、(2)の条件を満たす場合を考えているので、 $V_1$ と $V_3$ の共通部分は、 $V_1$ と $V_2$ と $V_3$ の共通部分と一致するので、体積は等しい。

以上から、
\begin{eqnarray} V &=& S+S+S-T-T-U+U \\[5pt] &=& 3S-2T \\[5pt] \end{eqnarray}となる。

解答編 つづき

問題

(4) ひきつづき r は(2)の条件をみたすとする。 S と T を求め、 V の体積を決定せよ。

(4)
S は、半径が r の半球2つと、底面が半径 r の円で高さが $1$ の円柱を合わせた図形の体積なので
\begin{eqnarray} S &=& \frac{4}{3}\pi r^3 +\pi r^2\times 1 \\[5pt] &=& \frac{4}{3}\pi r^3 +\pi r^2 \\[5pt] \end{eqnarray}となる。

$V_1$ と $V_2$ を $z=z_0$ で切る（ $-r\leqq z_0\leqq r$ ）と、断面は次のようになる。

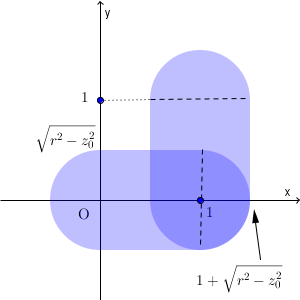
この共通部分は、半径 $\sqrt{r^2-z_0^2}$ の円の $\dfrac{3}{4}$ と、1辺が $\sqrt{r^2-z_0^2}$ の正方形なので、共通部分の体積は
\begin{eqnarray} T &=& \int_{-r}^r \left(\frac{3}{4} \pi+1\right) (r^2-z^2) dz \\[5pt] &=& \left(\frac{3}{4} \pi+1\right) \times 2\int_0^r (r^2-z^2) dz \\[5pt] &=& \left(\frac{3}{2} \pi+2\right) \left[ r^2z-\frac{1}{3}z^3 \right]_0^r \\[5pt] &=& \left(\frac{3}{2} \pi+2\right) \times \frac{2}{3}r^3 \\[5pt] &=& \left(\pi+\frac{4}{3} \right)r^3 \\[5pt] \end{eqnarray}となる。

よって、(3)より
\begin{eqnarray} V &=& 3S-2T \\[5pt] &=& 3\left(\frac{4}{3}\pi r^3 +\pi r^2\right)-2\left(\pi+\frac{4}{3} \right)r^3 \\[5pt] &=& 4\pi r^3 +3\pi r^2-2\pi r^3-\frac{8}{3}r^3 \\[5pt] &=& \left(2\pi -\frac{8}{3}\right)r^3 +3\pi r^2 \\[5pt] \end{eqnarray}となる。

以上から
\begin{eqnarray} S &=& \frac{4}{3}\pi r^3 +\pi r^2 \\[5pt] T &=& \left(\pi+\frac{4}{3} \right)r^3 \\[5pt] V &=& \left(2\pi -\frac{8}{3}\right)r^3 +3\pi r^2 \\[5pt] \end{eqnarray}となる。

（終）