共通テスト 数学I・数学A 2018年度プレテスト 第5問 解説

2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【選択問題】(第3問～第5問から2問選択)

問題編

問題

　ある日、太郎さんと花子さんのクラスでは、数学の授業で先生から次の問題1が宿題として出された。下の問いに答えよ。なお、円周上に異なる 2点をとった場合、弧は二つできるが、本問題において、弧は二つあるうちの小さい方を指す。

問題1
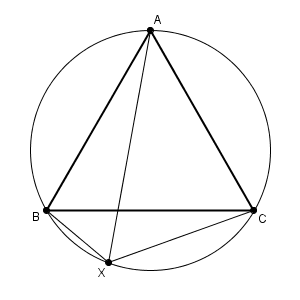
　正三角形 ABC の外接円の弧BC上に点X があるとき、 $\mathrm{ AX=BX+CX }$ が成り立つことを証明せよ。

(1) 問題1は次のような構想をもとにして証明できる。

　線分AX 上に $\mathrm{ BX = B'X }$ となる点 $\mathrm{ B' }$ をとり、 B と $\mathrm{ B' }$ を結ぶ。
$\mathrm{ AX = AB'+ B'X }$ なので、 $\mathrm{ AX=BX+CX }$ を示すには、 $\mathrm{ AB'=CX }$ を示せばよく、 $\mathrm{ AB' = CX }$ を示すには、二つの三角形 $\myBox{ア}$ と $\myBox{イ}$ が合同であることを示せばよい。

　$\myBox{ア}$, $\myBox{イ}$ に当てはまるものを、次の 0 ～ 7 のうちからも一つずつ選べ。ただし、 $\mybox{ア}$, $\mybox{イ}$ の解答の順序は問わない。

　0: $\triangle \mathrm{ ABB' }$
　1: $\triangle \mathrm{ AB'C }$
　2: $\triangle \mathrm{ ABX }$
　3: $\triangle \mathrm{ AXC }$

　4: $\triangle \mathrm{ BCB' }$
　5: $\triangle \mathrm{ BXB' }$
　6: $\triangle \mathrm{ B'XC }$
　7: $\triangle \mathrm{ CBX }$

---

　太郎さんたちは、次の日の数学の授業で問題1を証明した後、点X が弧BC 上にないときについて先生に質問をした。その質問に対して先生は、一般に次の定理が成り立つことや、その定理と問題1で証明したことを使うと、下の問題2が解決できることを教えてくれた。

定理
　平面上の点X と正三角形ABC の各頂点からの距離 AX, BX, CX について、点X が三角形ABC の外接円の弧BC 上にないときは、 $\mathrm{ AX\lt BX+CX }$ が成り立つ。

問題2
　三角形PQR について、各頂点からの距離の和 $\mathrm{ PY+QY+RY }$ が最小になる点 Y はどのような位置にあるかを求めよ。

(2) 太郎さんと花子さんは問題2について、次のような会話をしている。

• 問題1で証明したことは、二つの線分 BX と CX の長さの和を一つの線分 AX の長さに置き換えられるってことだよね。
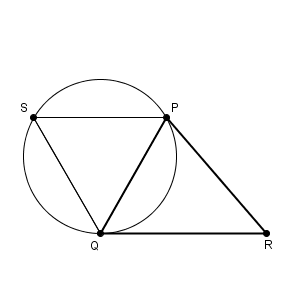
• 例えば、下の図の三角形PQR で辺PQ を 1辺とする正三角形をかいてみたらどうかな。ただし、辺QR を最も長い辺とするよ。 辺PQ に関して点R とは反対側に点S をとって、正三角形PSQ をかき、その外接円をかいてみようよ。

• 正三角形PSQ の外接円の弧PQ 上に点T をとると、PT とQT の長さの和は線分 $\myBox{ウ}$ の長さに置き換えられるから、 $\mathrm{ PT + QT + RT } =\mybox{ウ}+\mathrm{ RT }$ になるね。
• 定理と問題1で証明したことを使うと問題2の点Y は、点 $\myBox{エ}$ と点 $\myBox{オ}$ を通る直線と $\myBox{カ}$ との交点になることが示せるよ。
• でも、 $\angle \mathrm{ QPR }$ が $\myBox{キ}^{\circ}$ より大きいときは、点 $\mybox{エ}$ と点 $\mybox{オ}$ を通る直線と $\mybox{カ}$ が交わらないから、 $\angle \mathrm{ QPR }$ が $\myBox{キ}^{\circ}$ より小さいときという条件がつくよね。
• では、 $\angle \mathrm{ QPR }$ が $\mybox{キ}^{\circ}$ より大きいときは、点Y はどのような点になるのかな。

(i) $\myBox{ウ}$ に当てはまるものを、次の 0 ～ 5 のうちから一つ選べ。

　0: PQ
　1: PS
　2: QS

　3: RS
　4: RT
　5: ST

(ii) $\myBox{エ}$, $\myBox{オ}$ に当てはまるものを、次の 0 ～ 4 のうちから一つずつ選べ。ただし、 $\mybox{エ}$, $\mybox{オ}$ の解答の順序は問わない。

　0: P
　1: Q
　2: R
　3: S
　4: T

(iii) $\myBox{カ}$ に当てはまるものを、次の 0 ～ 5 のうちから一つ選べ。

　0: 辺PQ
　1: 辺PS
　2: 辺QS

　3: 弧PQ
　4: 弧PS
　5: 弧QS

(iv) $\myBox{キ}$ に当てはまるものを、次の 0 ～ 6 のうちから一つ選べ。

　0: 30
　1: 45
　2: 60
　3: 90

　4: 120
　5: 135
　6: 150

(v) $\angle \mathrm{ QPR }$ が $\mybox{キ}^{\circ}$ より「小さいとき」と「大きいとき」の点Y について正しく述べたものを、それぞれ次の 0～6 のうちから一つずつ選べ。ただし、同じものを選んでもよい。

　小さいとき $\myBox{ク}$
　大きいとき $\myBox{ケ}$

　0: 点Y は、三角形PQR の外心である。

　1: 点Y は、三角形PQR の内心である。

　2: 点Y は、三角形PQR の重心である。

　3: 点Y は、 $\angle \mathrm{ PYR }=\angle \mathrm{ QYP }=\angle \mathrm{ RYQ }$ となる点である。

　4: 点Y は、 $\angle \mathrm{ PQY }+\angle \mathrm{ PRY }+\angle \mathrm{ QPR }=180^{\circ}$ となる点である。

　5: 点Y は、三角形PQR の三つの辺のうち、最も短い辺を除く二つの辺の交点である。

　6: 点Y は、三角形PQR の三つの辺のうち、最も長い辺を除く二つの辺の交点である。

考え方

有名な図形問題ではありますが、最後は難易度が高いです。

(1)は、 $\mathrm{ B' }$ の場所が正しく把握できれば、正解は導けるでしょう。証明までできたほうがいいですが、形から推測することはできます。

(2)は、(i)(ii)(iii)は、図で示された状況だけを考えます。置き換えた後の式を見れば、線分の和が最小になるときは、図形からすぐにわかるでしょう。

(iv)は、境い目となるときがどんなときかを考えましょう。(v)の前半は、(iii)までに考えた内容が使えます。後半は、予想することはできますが、正確に証明しようとするとなかなかハードです。証明まで完成して自信をもって答えを出せる人は、すごく少ないでしょう。

【選択問題】(第3問～第5問から2問選択)

解答編

問題

　ある日、太郎さんと花子さんのクラスでは、数学の授業で先生から次の問題1が宿題として出された。下の問いに答えよ。なお、円周上に異なる 2点をとった場合、弧は二つできるが、本問題において、弧は二つあるうちの小さい方を指す。

問題1
　正三角形 ABC の外接円の弧BC上に点X があるとき、 $\mathrm{ AX=BX+CX }$ が成り立つことを証明せよ。

(1) 問題1は次のような構想をもとにして証明できる。

　線分AX 上に $\mathrm{ BX = B'X }$ となる点 $\mathrm{ B' }$ をとり、 B と $\mathrm{ B' }$ を結ぶ。
$\mathrm{ AX = AB'+ B'X }$ なので、 $\mathrm{ AX=BX+CX }$ を示すには、 $\mathrm{ AB'=CX }$ を示せばよく、 $\mathrm{ AB' = CX }$ を示すには、二つの三角形 $\myBox{ア}$ と $\myBox{イ}$ が合同であることを示せばよい。

　$\myBox{ア}$, $\myBox{イ}$ に当てはまるものを、次の 0 ～ 7 のうちからも一つずつ選べ。ただし、 $\mybox{ア}$, $\mybox{イ}$ の解答の順序は問わない。

　0: $\triangle \mathrm{ ABB' }$
　1: $\triangle \mathrm{ AB'C }$
　2: $\triangle \mathrm{ ABX }$
　3: $\triangle \mathrm{ AXC }$

　4: $\triangle \mathrm{ BCB' }$
　5: $\triangle \mathrm{ BXB' }$
　6: $\triangle \mathrm{ B'XC }$
　7: $\triangle \mathrm{ CBX }$

解説

問題文にある $\mathrm{ B }'$ を加えてみると、図は次のようになります。

$\mathrm{ BX=B'X }$ となる点 $\mathrm{ B' }$ を線分AX 上にとりました。 $\mathrm{ AX=AB'+B'X }$ なので、 $\mathrm{ AX=BX+CX }$ を示すには、 $\mathrm{ AB'+B'X=BX+CX }$ を示せばいいですね。また、 $\mathrm{ BX=B'X }$ なので、 $\mathrm{ AB'=CX }$ が示せればいいです。

この線分を含む三角形を探してみましょう。 $\mathrm{ AB' }$ を含むものは、 $\triangle \mathrm{ ABB' }$ と $\triangle \mathrm{ AB'C }$ がありますが、 CX を含む三角形と合同であるように見えるものにしぼると、 $\triangle \mathrm{ ABB' }$ だと考えられます。また、 CX を含むほうは $\triangle \mathrm{ CBX }$ と考えられます。これらが合同であることを確かめてみましょう。

$\triangle \mathrm{ ABB' }$ と $\triangle \mathrm{ CBX }$ について、三角形ABC は正三角形だから、 $\mathrm{ AB=CB }$ …① が成り立ちます。また、円周角の定理から、弧AB に対する円周角は等しいので、 $\angle \mathrm{ BXB' }=\angle \mathrm{ BCA }=60^{\circ}$ だから、三角形 $\mathrm{ BB'X }$ は正三角形です。なので、 $\mathrm{ BB'=BX }$ …②が成り立ちます。また、 $\angle \mathrm{ ABB' }$ も $\angle \mathrm{ CBX }$ も、 $60^{\circ}-\angle \mathrm{ B'BC }$ と表すことができるので、 $\angle \mathrm{ ABB' }=\angle \mathrm{ CBX }$ …③が成り立ちます。

以上から、①②③から、2組の辺とその間の角がそれぞれ等しいので、 $\triangle \mathrm{ ABB' }\equiv\triangle \mathrm{ CBX }$ であることがわかります。

よって、 $\mathrm{ AB'=CX }$ であり、 $\mathrm{ AX=BX+CX }$ であることも示せました。

解答

アイ：0・7

解答編 つづき

問題

　太郎さんたちは、次の日の数学の授業で問題1を証明した後、点X が弧BC 上にないときについて先生に質問をした。その質問に対して先生は、一般に次の定理が成り立つことや、その定理と問題1で証明したことを使うと、下の問題2が解決できることを教えてくれた。

定理
　平面上の点X と正三角形ABC の各頂点からの距離 AX, BX, CX について、点X が三角形ABC の外接円の弧BC 上にないときは、 $\mathrm{ AX\lt BX+CX }$ が成り立つ。

問題2
　三角形PQR について、各頂点からの距離の和 $\mathrm{ PY+QY+RY }$ が最小になる点 Y はどのような位置にあるかを求めよ。

(2) 太郎さんと花子さんは問題2について、次のような会話をしている。

• 問題1で証明したことは、二つの線分 BX と CX の長さの和を一つの線分 AX の長さに置き換えられるってことだよね。
• 例えば、下の図の三角形PQR で辺PQ を 1辺とする正三角形をかいてみたらどうかな。ただし、辺QR を最も長い辺とするよ。 辺PQ に関して点R とは反対側に点S をとって、正三角形PSQ をかき、その外接円をかいてみようよ。

• 正三角形PSQ の外接円の弧PQ 上に点T をとると、PT とQT の長さの和は線分 $\myBox{ウ}$ の長さに置き換えられるから、 $\mathrm{ PT + QT + RT } =\mybox{ウ}+\mathrm{ RT }$ になるね。
• 定理と問題1で証明したことを使うと問題2の点Y は、点 $\myBox{エ}$ と点 $\myBox{オ}$ を通る直線と $\myBox{カ}$ との交点になることが示せるよ。
• でも、 $\angle \mathrm{ QPR }$ が $\myBox{キ}^{\circ}$ より大きいときは、点 $\mybox{エ}$ と点 $\mybox{オ}$ を通る直線と $\mybox{カ}$ が交わらないから、 $\angle \mathrm{ QPR }$ が $\myBox{キ}^{\circ}$ より小さいときという条件がつくよね。
• では、 $\angle \mathrm{ QPR }$ が $\mybox{キ}^{\circ}$ より大きいときは、点Y はどのような点になるのかな。

(i) $\myBox{ウ}$ に当てはまるものを、次の 0 ～ 5 のうちから一つ選べ。

　0: PQ
　1: PS
　2: QS

　3: RS
　4: RT
　5: ST

解説

花子さんが初めに言ってるように、問題1では、「二つの線分 BX と CX の長さの和を一つの線分 AX の長さに置き換えられる」ことを示しています。これを活かすことを考えます。

次の太郎さんの発言では、次の図で考えてみよう、と言っているので、ひとまず、次の図の場合だけで考えてみます。

$\mathrm{ PT+QT+ST }$ というように、動くものが3つもあると大変ですが、問題1を使えば、このうちの2つを1つに置き換えられるのでした。そうすれば、動くものが減って、考えやすくなりそうです。

花子さんの2回目の発言では、正三角形PSQ の外接円の弧PQ 上に点T をとる、と言ってますね。これを図にかき加えると、次のようになります。

こうすれば、先ほどの問題1の内容が使えます。 A, B, C, X が S, P, Q, T になったと考えれば、 $\mathrm{ PT+QT }$ は $\mathrm{ ST }$ に置き換えられることがわかります。

解答

ウ：5

解答編 つづき

問題

(ii) $\myBox{エ}$, $\myBox{オ}$ に当てはまるものを、次の 0 ～ 4 のうちから一つずつ選べ。ただし、 $\mybox{エ}$, $\mybox{オ}$ の解答の順序は問わない。

　0: P
　1: Q
　2: R
　3: S
　4: T

(iii) $\myBox{カ}$ に当てはまるものを、次の 0 ～ 5 のうちから一つ選べ。

　0: 辺PQ
　1: 辺PS
　2: 辺QS

　3: 弧PQ
　4: 弧PS
　5: 弧QS

解説

先ほどの問題を利用すると、点T が弧PQ 上にあるときは考えやすいですね。 $\mathrm{ PT+QT+RT }$ は $\mathrm{ ST+RT }$ と置き換えられますが、これが最短になるのは、次のようなときです。

この図の場合では、 $\mathrm{ ST+RT }$ が最小となるのは、S, T, R が同一直線上にあるときです。このときに、 $\mathrm{ PT+QT+RT }$ も最小となります。これは、言い換えれば、 S, R を結ぶ直線と、弧PQ との交点、ということですね。このとき、 $\mathrm{ PT+QT+RT }$ は、線分SR の長さと等しくなります。

解答は選択式なのでこれでも答えは出せるのですが、点T が弧PQ 上にないときも考えておきましょう。この場合は、事前に紹介されている定理を使います。この定理を使えば、 $\mathrm{ ST\lt PT+QT }$ となることがわかります。よって、この場合は、 $\mathrm{ PT+QT+RT }$ は、 $\mathrm{ ST+TR }$ よりも大きくなるので、もちろん、線分 SR よりも大きくなってしまいます。

以上から、点Y は、2点 R, S を結ぶ直線と、弧PQ との交点、となることがわかります。

解答

エオ：2・3
カ：3

解答編 つづき

問題

(iv) $\myBox{キ}$ に当てはまるものを、次の 0 ～ 6 のうちから一つ選べ。

　0: 30
　1: 45
　2: 60
　3: 90

　4: 120
　5: 135
　6: 150

解説

花子さんの最後の発言の通り、 $\angle \mathrm{ QPR }$ の大きさによっては、 SR と弧 PQ が交わらないことがあります。その境界はどこにあるかを考えるには、交わる・交わらないの境い目となる場合を想像してみましょう。そうすると、次のような図であることがわかります。

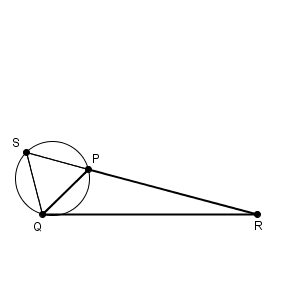
S, P, R が一直線に並んでしまうときです。これ以上 $\angle \mathrm{ QPR }$ が大きくなると、直線 SR は弧PQ の外に行ってしまい、交わることはありません。逆に、小さければ、交わるようになります。よって、境い目はこの場合で、 $\angle \mathrm{ QPS }=60^{\circ}$ なので、このときの $\angle \mathrm{ QPR }$ は $120^{\circ}$ であることがわかります。

解答

キ：4

解答編 つづき

問題

(v) $\angle \mathrm{ QPR }$ が $\mybox{キ}^{\circ}$ より「小さいとき」と「大きいとき」の点Y について正しく述べたものを、それぞれ次の 0～6 のうちから一つずつ選べ。ただし、同じものを選んでもよい。

　小さいとき $\myBox{ク}$
　大きいとき $\myBox{ケ}$

　0: 点Y は、三角形PQR の外心である。

　1: 点Y は、三角形PQR の内心である。

　2: 点Y は、三角形PQR の重心である。

　3: 点Y は、 $\angle \mathrm{ PYR }=\angle \mathrm{ QYP }=\angle \mathrm{ RYQ }$ となる点である。

　4: 点Y は、 $\angle \mathrm{ PQY }+\angle \mathrm{ PRY }+\angle \mathrm{ QPR }=180^{\circ}$ となる点である。

　5: 点Y は、三角形PQR の三つの辺のうち、最も短い辺を除く二つの辺の交点である。

　6: 点Y は、三角形PQR の三つの辺のうち、最も長い辺を除く二つの辺の交点である。

解答

(iv)で見た通り、境い目は $120^{\circ}$ です。ここで場合を分けて考えていきましょう。

まず、 $\angle \mathrm{ QPR }$ が $120^{\circ}$ より小さい場合ですが、これは、今まで考えてきた状況ですね。このときの点 Y は、次のように、直線SR と弧 PQ の交点です。

が、もちろん、これがそのまま選択肢になっているのは、ないですね。ただ、この図をよく見ると、四角形 SPYQ は円に内接しているため、 $\angle \mathrm{ PYQ }=120^{\circ}$ です。また、円周角の定理から、 $\angle \mathrm{ PYS }$, $\angle \mathrm{ QYS }$ はともに $60^{\circ}$ なので、 $\angle \mathrm{ PYR }$, $\angle \mathrm{ QYR }$ はともに $120^{\circ}$ となります。よって、\[ \angle \mathrm{ PYR }=\angle \mathrm{ QYP }=\angle \mathrm{ RYQ } \]が成り立ちます。

次に、 $\angle \mathrm{ QPR }$ が $120^{\circ}$ より大きい場合を考えましょう。

答えの予想を立てる上で、境界の状況を考えてみましょう。 $\angle \mathrm{ QPR }=120^{\circ}$ の状況と、これより少し大きくなった時の状況から、選択肢を絞っていきましょう。

$\mathrm{ PY+QY+RY }$ が最短となる Y がどこに来るかは、120度のときから少しずつ大きくなるように変形していけば、少しずつずれていくんじゃないか、と予想できます。なので、この時点でぜんぜん別の場所にあるものは、選択肢から外していってもいいでしょう。

120度のときには、点Y は点P のところにいるので、三角形 PQR の外心・内心・重心ということはありません。また、 $\angle \mathrm{ PQY }+\angle \mathrm{ PRY }+\angle \mathrm{ QPR }=180^{\circ}$ も成り立たないし、「最も短い辺を除く二つの辺の交点」ということもありません。3の「 $\angle \mathrm{ PYR }=\angle \mathrm{ QYP }=\angle \mathrm{ RYQ }$ となる点」は、たまたまこの120度の場合だけ定義だけないかもしれないので、一応残しておきます。6の「最も長い辺を除く二つの辺の交点」は今の状況にあってます。

これを踏まえて、考えていきます。120度未満のときと同じようにして、点 T が弧 PQ 上にあるときを考えましょう。

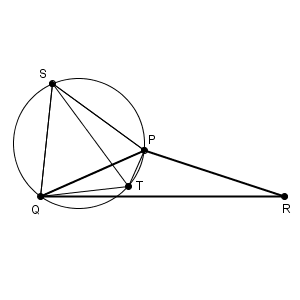
このとき、 $\mathrm{ PT+QT=ST }$ なので、 $\mathrm{ ST+RT }$ が小さくなるときを考えればよく、弧 $\mathrm{ PQ }$ 上の場合だけを考えれば、点 P であることがわかります。そのため、どうやら、6の「最も長い辺を除く二つの辺の交点」が正しそうです。

正確に示すならば、点T が弧PQ 上にないときも考えなければいけません。この場合は自力で証明するのは難しいですが、以下のようにして示すことができます。

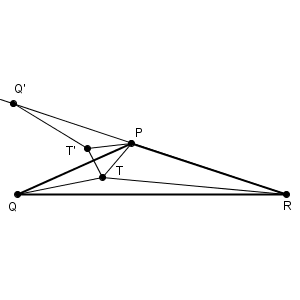
上の図のように、線分PR の延長線上に、 $\mathrm{ PQ=PQ' }$ となる点をとります。このとき、 $\angle \mathrm{ QPQ' }$ は60度未満になることがわかります。このことが後で効いてきます。また、点T を点P 以外の点とします。これを、点P を中心に、 $\angle \mathrm{ QPQ' }$ だけ回転した点 $\mathrm{ T' }$ をとります。回転の方向は、 Q から $\mathrm{ Q' }$ へ移すのと同じ方向です。 P, Q, T が一直線上にないときは、 $\triangle \mathrm{ PQT }\equiv \triangle \mathrm{ PQ'T' }$ となります。

このとき、 $\angle \mathrm{ TPT' }$ は $\angle \mathrm{ QPQ' }$ と一致し、60度未満であることから、 $\mathrm{ PT }\gt \mathrm{ TT' }$ であることがわかります。また、 $\mathrm{ QT }=\mathrm{ Q'T' }$ なので、
\begin{eqnarray} & & \mathrm{ PT+QT+RT } \\[5pt] &\gt & \mathrm{ TT'+Q'T'+RT } \\[5pt] &\geqq & \mathrm{ Q'R } \\[5pt] &= & \mathrm{ QP }+\mathrm{ PR } \\[5pt] \end{eqnarray}となります。これより、 $\angle \mathrm{ QPR }$ が $120^{\circ}$ より大きい場合は、 $\mathrm{ PY+QY+RY }$ が最小となる点Y は点P のとき、言い換えれば、「三角形PQR の三つの辺のうち、最も長い辺を除く二つの辺の交点」のときであることがわかります。

解答

ク：3
ケ：6