センター試験 数学II・数学B 2019年度追試 第1問 [1] 解説
【必答問題】
問題編
問題
a を実数とする。座標平面上で、点 $(3,1)$ を中心とする半径 $1$ の円を C とし、直線 $y=ax$ を $\ell$ とする。
(1) 円 C の方程式は\[ x^2+y^2-\myBox{ア}x-\myBox{イ}y+\myBox{ウ}=0 \]である。
(2) 円 C と直線 $\ell$ が接するのは\[ a=\myBox{エ},\ \frac{\myBox{オ} }{\myBox{カ} } \]のときである。
$a=\dfrac{\mybox{オ} }{\mybox{カ} }$ のとき、 $C$ と $\ell$ の接点を通り、 $\ell$ に垂直な直線の方程式は\[ y=\frac{\myBox{キク} }{\myBox{ケ} }x+\myBox{コ} \]である。ただし、 $\myBox{キク}$, $\myBox{ケ}$, $\myBox{コ}$ は、文字 a を用いない形で答えること。
(3) 円 C と直線 $\ell$ が異なる2点 A, B で交わるとき、二つの交点を結ぶ線分 AB の長さは\[ \myBox{サ}\sqrt{\frac{\myBox{シ}a-\myBox{ス}a^2}{a^2+1} } \]である。また、 AB の長さが $2$ となるのは\[ a=\dfrac{\myBox{セ} }{\myBox{ソ} } \]のときである。
考え方
(2)は、二次方程式のように解くこともできますが、図形と方程式の分野で学ぶ内容を使って解くことができます。円を、中心からの距離が一定である点の集まり、と考えるとわかりやすいでしょう。いろいろな解き方があるので、得意なやり方で考えるといいでしょう。
(3)の最後の部分は、その前に求めた式を使うこともできますし、使わずに解くこともできます。
【必答問題】
解答編
問題
a を実数とする。座標平面上で、点 $(3,1)$ を中心とする半径 $1$ の円を C とし、直線 $y=ax$ を $\ell$ とする。
(1) 円 C の方程式は\[ x^2+y^2-\myBox{ア}x-\myBox{イ}y+\myBox{ウ}=0 \]である。
解説
中心が $(3,1)$ で半径が $1$ の円の方程式は
\begin{eqnarray}
(x-3)^2+(y-1)^2 &=& 1^2 \\[5pt]
x^2-6x+9+y^2-2y+1-1 &=& 0 \\[5pt]
x^2+y^2-6x-2y+9 &=& 0 \\[5pt]
\end{eqnarray}となります。
解答
アイウ:629
参考
解答編 つづき
(2) 円 C と直線 $\ell$ が接するのは\[ a=\myBox{エ},\ \frac{\myBox{オ} }{\myBox{カ} } \]のときである。
解説
円 $C$ と直線 $\ell$ が接するのは、直線と円 $C$ の中心 $(3,1)$ との距離が $1$ のときです。点と直線との距離の公式から、
\begin{eqnarray}
\frac{|3a-1|}{\sqrt{a^2+(-1)^2} } &=& 1 \\[5pt]
|3a-1| &=& \sqrt{a^2+1} \\[5pt]
\end{eqnarray}を解けばいいことがわかります。両辺は正なので
\begin{eqnarray}
(3a-1)^2 &=& a^2+1 \\[5pt]
9a^2-6a+1 &=& a^2+1 \\[5pt]
8a^2-6a &=& 0 \\[5pt]
a &=& 0, \frac{3}{4} \\[5pt]
\end{eqnarray}となります。
他の解き方としては、接線の方程式の公式を用いる方法もあります。中心が原点ではないので、少し式が複雑です。また、 $y=ax$ を円 $C$ の式に代入して、重解を持つときを考える、という方法もあります。さらに別の方法として、次のように図形的に考えるやり方もあります。
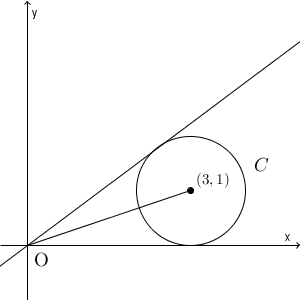
図は上のようになっています。中心が $(3,1)$ で半径が $1$ なので、 $y=0$ が円に接することはわかります。また、もう1つの接線の傾きは、 $(3,1)$, $(0,0)$, $(3,0)$ を結んでできる角を $\alpha$ としたときに、 $\tan 2\alpha$ と書けるので、
\begin{eqnarray}
\tan 2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}=\frac{\frac{2}{3} }{1-\frac{1}{3^2} }=\frac{3}{4}
\end{eqnarray}と求めることもできます。
解答
エ:0
オカ:34
参考
解答編 つづき
$a=\dfrac{\mybox{オ} }{\mybox{カ} }$ のとき、 $C$ と $\ell$ の接点を通り、 $\ell$ に垂直な直線の方程式は\[ y=\frac{\myBox{キク} }{\myBox{ケ} }x+\myBox{コ} \]である。ただし、 $\myBox{キク}$, $\myBox{ケ}$, $\myBox{コ}$ は、文字 a を用いない形で答えること。
解説
$y=\dfrac{3}{4}x$ に垂直な直線の傾きは、 $-\dfrac{4}{3}$ です。また、 $C$ と $\ell$ の接点を通り、接線に垂直な直線は円の中心を通ります。
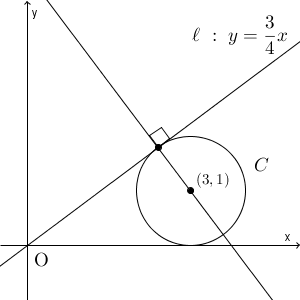
よって、この直線の方程式は
\begin{eqnarray}
y-1 &=& -\frac{4}{3}(x-3) \\[5pt]
y &=& -\frac{4}{3}x+4+1 \\[5pt]
&=& -\frac{4}{3}x+5 \\[5pt]
\end{eqnarray}と求められます。
円の中心を通ることに気づかなくても、 $y=\dfrac{3}{4}x$ を円 $C$ の方程式に代入して、接点を求めてから計算することもできます。
解答
キクケ:-43
コ:5
参考
解答編 つづき
(3) 円 C と直線 $\ell$ が異なる2点 A, B で交わるとき、二つの交点を結ぶ線分 AB の長さは\[ \myBox{サ}\sqrt{\frac{\myBox{シ}a-\myBox{ス}a^2}{a^2+1} } \]である。また、 AB の長さが $2$ となるのは\[ a=\dfrac{\myBox{セ} }{\myBox{ソ} } \]のときである。
解説
円 $C$ の中心 $(3,1)$ と直線 $\ell$ との距離は、(2)で求めたように、 $\dfrac{|3a-1|}{\sqrt{a^2+1} }$ です。円 $C$ と直線 $\ell$ が異なる2点 A, B で交わるのは、この距離が $1$ 未満となるときです。
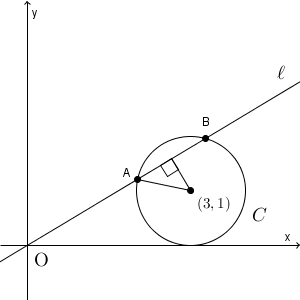
このときの線分 AB の長さは、三平方の定理から
\begin{eqnarray}
& &
2\sqrt{1^2-\left(\dfrac{|3a-1|}{\sqrt{a^2+1} }\right)^2} \\[5pt]
&=&
2\sqrt{1-\dfrac{9a^2-6a+1}{a^2+1} } \\[5pt]
&=&
2\sqrt{\dfrac{(a^2+1)-(9a^2-6a+1)}{a^2+1} } \\[5pt]
&=&
2\sqrt{\dfrac{6a-8a^2}{a^2+1} } \\[5pt]
\end{eqnarray}となります。これが $2$ となるのは
\begin{eqnarray}
2\sqrt{\dfrac{6a-8a^2}{a^2+1} } &=& 2 \\[5pt]
\dfrac{6a-8a^2}{a^2+1} &=& 1 \\[5pt]
6a-8a^2 &=& a^2+1 \\[5pt]
9a^2-6a+1 &=& 0 \\[5pt]
(3a-1)^2 &=& 0 \\[5pt]
a &=& \dfrac{1}{3} \\[5pt]
\end{eqnarray}のときだとわかります。
流れとして、 AB の長さを $a$ を用いた式で表したので、 $\mathrm{ AB }=2$ となるのは、上のように解くのが自然でしょう。しかし、図形的に考えると、円 $C$ の半径が $1$ なのだから、 AB が $2$ になるということは、 AB が直径となるとき、つまり、直線 $\ell$ が円 $C$ の中心を通るときです。そう考えると、 $\ell$ の方程式は $y=\dfrac{1}{3}x$ だとすぐにわかります。
問題文が「また、 AB の長さが~」となっていますが、ここが「よって、 AB の長さが~」となっていれば、その直前で求めた式を利用して解くことが想定されていると考えられます。「また、」という記述から、話が変わっているニュアンスが含まれているので、直前で求めた式を利用することは、「よって、」と書かれているときほど想定されていない、と深読みできるかもしれません。
解答
サシス:268
セソ:13





