センター試験数学II・数学B 2019年度第2問解説

🕒 2019/01/20 🔄 2023/05/01

【必答問題】

問題編

問題

　p, q を実数とし、関数 $f(x)=x^3+px^2+qx$ は $x=-1$ で極値 $2$ をとるとする。また、座標平面上の曲線 $y=f(x)$ を $C$, 放物線 $y=-kx^2$ を $D$, 放物線 $D$ 上の点 $(a,-ka^2)$ を A とする。ただし、 $k\gt 0$, $a\gt 0$ である。

(1) 関数 $f(x)$ が $x=-1$ で極値をとるので、 $f'(-1)=\myBox{ア}$ である。これと $f(-1)=2$ より、 $p=\myBox{イ}$, $q=\myBox{ウエ}$ である。よって、 $f(x)$ は $x=\myBox{オ}$ で極小値 $\myBox{カキ}$ をとる。

(2) 点 A における放物線 $D$ の接線を $\ell$ とする。 $D$ と $\ell$ および $x$ 軸で囲まれた図形の面積 $S$ を $a$ と $k$ を用いて表そう。

　$\ell$ の方程式は\[ y=\myBox{クケ}kax+ka^{\myBox{コ} }\quad \cdots ① \]と表せる。 $\ell$ と $x$ 軸の交点の $x$ 座標は $\dfrac{\myBox{サ} }{\myBox{シ} }$ であり、 $D$ と $x$ 軸および直線 $x=a$ で囲まれた図形の面積は $\dfrac{k}{\myBox{ス} }a^{\myBox{セ} }$ である。よって、 $S=\dfrac{k}{\myBox{ソタ} }a^{\mybox{セ} }$ である。

(3) さらに、点 A が曲線 $C$ 上にあり、かつ(2)の接線 $\ell$ が $C$ にも接するとする。このときの(2)の $S$ の値を求めよう。

　A が $C$ 上にあるので、 $k=\dfrac{\myBox{チ} }{\myBox{ツ} }-\myBox{テ}$ である。

　$\ell$ と $C$ の接線の $x$ 座標を $b$ とすると、 $\ell$ の方程式は $b$ を用いて\[ y=\myBox{ト} \left(b^2-\myBox{ナ}x\right)-\myBox{ニ}b^2 \quad \cdots ② \]と表される。②の右辺を $g(x)$ とおくと\[ f(x)-g(x)=\left(x-\myBox{ヌ}\right)^2 \left(x+\myBox{ネ}b\right) \]と因数分解されるので、 $a=-\mybox{ネ}b$ となる。①と②の表す直線の傾きを比較することにより、 $a^2=\dfrac{\myBox{ノハ} }{\myBox{ヒ} }$ である。

　したがって、求める $S$ の値は $\dfrac{\myBox{フ} }{\myBox{ヘホ} }$ である。

考え方

(1)は、微分の基本的な問題です。後半は、増減表をかいて考えましょう。

(2)は、図をかいてみると、どこを計算すればいいかわかりやすくなります。スセを求めるには積分を使いますが、その次の $S$ を求めるのは、積分を使わなくても構いません。

(3)は、どの直線・曲線を考えているのかわかりにくいですが、 $\ell$ に着目しながら考えていくとわかりやすいかもしれません。後半の計算は、微分・積分の計算というよりは、ただの式の値を求める計算になってしまっています。

【必答問題】

解答編

問題

　p, q を実数とし、関数 $f(x)=x^3+px^2+qx$ は $x=-1$ で極値 $2$ をとるとする。また、座標平面上の曲線 $y=f(x)$ を $C$, 放物線 $y=-kx^2$ を $D$, 放物線 $D$ 上の点 $(a,-ka^2)$ を A とする。ただし、 $k\gt 0$, $a\gt 0$ である。

(1) 関数 $f(x)$ が $x=-1$ で極値をとるので、 $f'(-1)=\myBox{ア}$ である。これと $f(-1)=2$ より、 $p=\myBox{イ}$, $q=\myBox{ウエ}$ である。よって、 $f(x)$ は $x=\myBox{オ}$ で極小値 $\myBox{カキ}$ をとる。

解説

関数 $f(x)$ が $x=-1$ で極値をとることから、 $f'(-1)=0$ がわかります。 $f'(x)=3x^2+2px+q$ なので、\[ 3-2p+q=0 \]が得られます。

また、 $f(-1)=2$ であることから、\[ -1+p-q=2 \]であることがわかります。

2つの式を辺々足すと\[ p=0 \]が得られ、 $q=-3$ となることがわかります。

よって、 $f(x)=x^3-3x$ となります。 $f'(x)=3x^2-3=3(x+1)(x-1)$ なので、 $f'(x)=0$ とすると、 $x=\pm 1$ となります。よって、増減表は次のようになります。

\begin{array}{c|ccccc} x & \cdots & -1 & \cdots & 1 & \cdots \\ \hline f'(x) & + & 0 & - & 0 & + \\ \hline f(x) & \nearrow & & \searrow & & \nearrow \end{array}増減表より、極小値は $x=1$ のときにとることがわかります。その値は $f(1)=1-3=-2$ となります。

解答

ア：0
イ：0
ウエ：-3
オ：1
カキ：-2

解答編つづき

問題

(2) 点 A における放物線 $D$ の接線を $\ell$ とする。 $D$ と $\ell$ および $x$ 軸で囲まれた図形の面積 $S$ を $a$ と $k$ を用いて表そう。

　$\ell$ の方程式は\[ y=\myBox{クケ}kax+ka^{\myBox{コ} }\quad \cdots ① \]と表せる。

解説

$y=-kx^2$ を微分すると $y'=-2kx$ なので、点A $(a,-ka^2)$ での接線の傾きは $-2ka$ となります。この接線は点 A を通るので
\begin{eqnarray} y-(-ka^2) &=& -2ka(x-a) \\[5pt] y &=& -2kax+2ka^2-ka^2 \\[5pt] &=& -2kax+ka^2 \\[5pt] \end{eqnarray}となります。

解答

クケ：-2
コ：2

解答編つづき

問題

$\ell$ と $x$ 軸の交点の $x$ 座標は $\dfrac{\myBox{サ} }{\myBox{シ} }$ であり、 $D$ と $x$ 軸および直線 $x=a$ で囲まれた図形の面積は $\dfrac{k}{\myBox{ス} }a^{\myBox{セ} }$ である。よって、 $S=\dfrac{k}{\myBox{ソタ} }a^{\mybox{セ} }$ である。

解説

$y=-2kax+ka^2$ で $y=0$ とすると $x=\dfrac{ka^2}{2ka}=\dfrac{a}{2}$ なので、 $\ell$ と $x$ 軸の交点の $x$ 座標は $\dfrac{a}{2}$ となります。

$D$ と $x$ 軸および直線 $x=a$ で囲まれた図形は、次のようになります。

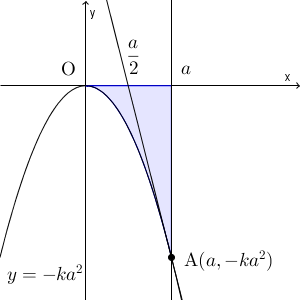
よって、この面積は
\begin{eqnarray} & & \int_0^a kx^2 dx \\[5pt] &=& \Big[ \frac{kx^3}{3} \Big]_0^a \\[5pt] &=& \frac{ka^3}{3} \\[5pt] \end{eqnarray}となります。

$S$ を求めるには、さらにこれから底辺が $\dfrac{a}{2}$ で高さが $ka^2$ の三角形の面積を引けばいいので
\begin{eqnarray} S &=& \frac{ka^3}{3}-\frac{1}{2}\cdot \frac{a}{2}\cdot ka^2 \\[5pt] &=& \frac{ka^3}{3}-\frac{ka^3}{4} \\[5pt] &=& \frac{ka^3}{12} \\[5pt] \end{eqnarray}となります。

解答

サシ：a2
スセ：33
シタ：12

解答編つづき

問題

(3) さらに、点 A が曲線 $C$ 上にあり、かつ(2)の接線 $\ell$ が $C$ にも接するとする。このときの(2)の $S$ の値を求めよう。

　A が $C$ 上にあるので、 $k=\dfrac{\myBox{チ} }{\myBox{ツ} }-\myBox{テ}$ である。

解説

$(a,-ka^2)$ が $y=x^3-3x$ 上にあるので
\begin{eqnarray} -ka^2 &=& a^3-3a \\[5pt] -k &=& a-\frac{3}{a} \\[5pt] k &=& \frac{3}{a}-a \\[5pt] \end{eqnarray}が成り立ちます。

解答

チツテ：3aa

解答編つづき

問題

　$\ell$ と $C$ の接線の $x$ 座標を $b$ とすると、 $\ell$ の方程式は $b$ を用いて\[ y=\myBox{ト} \left(b^2-\myBox{ナ}x\right)-\myBox{ニ}b^2 \quad \cdots ② \]と表される。

解説

$\ell$ と $C$ の接線の $x$ 座標を $b$ とすると、接点の座標は $(b,b^3-3b)$ であり、接線の傾きは $f'(b)=3b^2-3$ なので、接線の方程式は
\begin{eqnarray} y-(b^3-3b) &=& (3b^2-3)(x-b) \\[5pt] y &=& 3(b^2-1)x-3b^3+3b+b^3-3b \\[5pt] &=& 3(b^2-1)x-2b^3 \\[5pt] \end{eqnarray}となります。 $\ell$ が $C$ とこの点で接するという条件から、 $\ell$ はこのようにも書けることになります。

解答

トナニ：312

解答編つづき

問題

②の右辺を $g(x)$ とおくと\[ f(x)-g(x)=\left(x-\myBox{ヌ}\right)^2 \left(x+\myBox{ネ}b\right) \]と因数分解されるので、 $a=-\mybox{ネ}b$ となる。①と②の表す直線の傾きを比較することにより、 $a^2=\dfrac{\myBox{ノハ} }{\myBox{ヒ} }$ である。

　したがって、求める $S$ の値は $\dfrac{\myBox{フ} }{\myBox{ヘホ} }$ である。

解説

\begin{eqnarray} f(x)-g(x) &=& (x^3-3x)-\{ 3(b^2-1)x-2b^3 \} \\[5pt] &=& x^3-3x-3(b^2-1)x+2b^3 \\[5pt] &=& x^3-3b^2x+2b^3 \\[5pt] &=& (x-b)(x^2+bx-2b^2) \\[5pt] &=& (x-b)(x-b)(x+2b) \\[5pt] &=& (x-b)^2(x+2b) \\[5pt] \end{eqnarray}と因数分解できます。

このことから、 $y=f(x)$ と $y=g(x)$ は、 $x=-2b$ で交わることがわかり、 $x=b$ で接することがわかります。ここで、点A は、 $y=f(x)$ （曲線C）上にあり、 $y=g(x)$ （直線 $\ell$ ）上にもあるので、 $f(a)-g(a)=0$ が成り立ちます。よって、 $a=b$ または $a=-2b$ となります。

ここで、直線 $\ell$ の式を2通りに書いたものを比べてみると
\begin{eqnarray} y &=& -2kax+ka^2 \\[5pt] y &=& 3(b^2-1)x-2b^3 \end{eqnarray}となります。1つ目は、(2)で見た、 $y=-fx^2$ と接するという条件が得られた式で、2つ目はさきほど得られた式です。表現は違いますが、同じ式です。1つ目の式から、定数項は正であるため、 $b$ は負となります。 $a$ は正なので、 $a=b$ となることはなく、 $a=-2b$ であることがわかります。

これをもとに傾きを考えると
\begin{eqnarray} -2ka &=& 3(b^2-1) \\[5pt] -2\left(\frac{3}{a}-a\right)a &=& 3 \left(\frac{a^2}{4}-1\right) \\[5pt] -6+2a^2 &=& \frac{3}{4}a^2-3 \\[5pt] \frac{5}{4}a^2 &=& 3 \\[5pt] a^2 &=& \frac{12}{5} \\[5pt] \end{eqnarray}となります。

よって、
\begin{eqnarray} S &=& \left(\frac{3}{a}-a\right)\cdot \frac{a^3}{12} \\[5pt] &=& \frac{a^2}{4}-\frac{a^4}{12} \\[5pt] &=& \frac{1}{4}\cdot \frac{12}{5}-\frac{1}{12}\cdot\frac{12^2}{5^2} \\[5pt] &=& \frac{3}{5}-\frac{12}{25} \\[5pt] &=& \frac{3}{25} \\[5pt] \end{eqnarray}となります。