センター試験 数学II・数学B 2019年度 第4問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
四角形 ABCD を底面とする四角錐 OABCD を考える。四角形 ABCD は、辺 AD と辺 BC が平行で、 $\mathrm{ AB=CD }$, $\mathrm{ \angle ABC=\angle BCD }$ を満たすとする。さらに、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$, $\overrightarrow{ \mathrm{ OC } }=\vec{c}$ として
\begin{eqnarray} |\vec{a}| &=& 1 \\[5pt] |\vec{b}| &=& \sqrt{3} \\[5pt] |\vec{c}| &=& \sqrt{5} \\[5pt] \vec{a}\cdot\vec{b} &=& 1 \\[5pt] \vec{b}\cdot\vec{c} &=& 3 \\[5pt] \vec{c}\cdot\vec{a} &=& 0 \\[5pt] \end{eqnarray}であるとする。(1) $\mathrm{ \angle AOC }=\myBox{アイ}^{\circ}$ により、三角形 OAC の面積は $\dfrac{\sqrt{\myBox{ウ} }}{\myBox{エ} }$ である。
(2) $\overrightarrow{ \mathrm{ BA } }\cdot \overrightarrow{ \mathrm{ BC } }=\myBox{オカ}$, $\Big| \overrightarrow{ \mathrm{ BA } } \Big|=\sqrt{\myBox{キ} }$, $\Big| \overrightarrow{ \mathrm{ BC } } \Big|=\sqrt{\myBox{ク} }$ であるから、 $\angle \mathrm{ ABC }=\myBox{ケコサ}^{\circ}$ である。さらに、辺 AD と辺 BC が平行であるから、 $\angle \mathrm{ BAD }=\angle \mathrm{ ADC }=\myBox{シス}^{\circ}$ である。よって、 $\overrightarrow{ \mathrm{ AD } }=\myBox{セ} \overrightarrow{ \mathrm{ BC } }$ であり\[ \overrightarrow{ \mathrm{ OD } }=\vec{a}-\myBox{ソ}\vec{b}+\myBox{タ}\vec{c} \]と表される。また、四角形 ABCD の面積は $\dfrac{\myBox{チ}\sqrt{\myBox{ツ} }}{\myBox{テ} }$ である。
(3) 三角形 OAC を底面とする三角錐 BOAC の体積 $V$ を求めよう。
3点 O, A, C の定める平面 $\alpha$ 上に、点 H を $\overrightarrow{ \mathrm{ BH } }\perp \vec{a}$ と $\overrightarrow{ \mathrm{ BH } }\perp \vec{c}$ が成り立つようにとる。 $\Big|\overrightarrow{ \mathrm{ BH } }\Big|$ は三角錐 BOAC の高さである。 H は $\alpha$ 上の点であるから、実数 s, t を用いて $\overrightarrow{ \mathrm{ OH } }=s\vec{a}+t\vec{c}$ の形に表される。
$\overrightarrow{ \mathrm{ BH } }\cdot{a}=\myBox{ト}$, $\overrightarrow{ \mathrm{ BH } }\cdot{c}=\mybox{ト}$ により、 $s=\myBox{ナ}$, $t=\dfrac{\myBox{ニ} }{\myBox{ヌ} }$ である。よって、 $\Big|\overrightarrow{ \mathrm{ BH } }\Big|=\dfrac{\sqrt{\myBox{ネ} }}{\myBox{ノ} }$ が得られる。したがって、(1)により、 $V=\dfrac{\myBox{ハ} }{\myBox{ヒ} }$ であることがわかる。
(4) (3)の $V$ を用いると、四角錐 OABCD の体積は $\myBox{フ}V$ と表せる。さらに、四角形 ABCD を底面とする四角錐 OABCD の高さは $\dfrac{\sqrt{\myBox{ヘ} }}{\myBox{ホ} }$ である。
考え方
空間ベクトルの問題ですが、(1)(2)では、あまり空間を意識する必要はありません。(2)では、四角形 ABCD を書いて考えてみましょう。
(3)では、内積を用いた計算です。それほど計算は多くありません。
(4)は、ベクトルの問題というよりも、図形の問題です。どこを底面とするか、視点を変えて考えましょう。体積から高さを求めるのもよくある手法です。体積の公式から逆算しましょう。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
四角形 ABCD を底面とする四角錐 OABCD を考える。四角形 ABCD は、辺 AD と辺 BC が平行で、 $\mathrm{ AB=CD }$, $\mathrm{ \angle ABC=\angle BCD }$ を満たすとする。さらに、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$, $\overrightarrow{ \mathrm{ OC } }=\vec{c}$ として
\begin{eqnarray} |\vec{a}| &=& 1 \\[5pt] |\vec{b}| &=& \sqrt{3} \\[5pt] |\vec{c}| &=& \sqrt{5} \\[5pt] \vec{a}\cdot\vec{b} &=& 1 \\[5pt] \vec{b}\cdot\vec{c} &=& 3 \\[5pt] \vec{c}\cdot\vec{a} &=& 0 \\[5pt] \end{eqnarray}であるとする。(1) $\mathrm{ \angle AOC }=\myBox{アイ}^{\circ}$ により、三角形 OAC の面積は $\dfrac{\sqrt{\myBox{ウ} }}{\myBox{エ} }$ である。
解説
$\vec{c}\cdot\vec{a}=0$ なので、 $\angle \mathrm{ AOC }=90^{\circ}$ です。よって、三角形 OAC の面積は
\begin{eqnarray}
\dfrac{\mathrm{ OA }\cdot \mathrm{ OC } }{2}=\frac{\sqrt{5} }{2}
\end{eqnarray}となります。
解答
アイ:90
ウエ:52
解答編 つづき
問題
(2) $\overrightarrow{ \mathrm{ BA } }\cdot \overrightarrow{ \mathrm{ BC } }=\myBox{オカ}$, $\Big| \overrightarrow{ \mathrm{ BA } } \Big|=\sqrt{\myBox{キ} }$, $\Big| \overrightarrow{ \mathrm{ BC } } \Big|=\sqrt{\myBox{ク} }$ であるから、 $\angle \mathrm{ ABC }=\myBox{ケコサ}^{\circ}$ である。
解説
\begin{eqnarray} \overrightarrow{ \mathrm{ BA } }\cdot \overrightarrow{ \mathrm{ BC } } &=& (\vec{a}-\vec{b})\cdot(\vec{c}-\vec{b}) \\[5pt] &=& \vec{a}\cdot \vec{c} -\vec{a}\cdot \vec{b} -\vec{b}\cdot \vec{c} +\vec{b}\cdot \vec{b} \\[5pt] &=& 0 -1 -3 +(\sqrt{3})^2 \\[5pt] &=& -1 \end{eqnarray}となります。また、
\begin{eqnarray}
\Big| \overrightarrow{ \mathrm{ BA } } \Big|^2
&=&
(\vec{a}-\vec{b})\cdot (\vec{a}-\vec{b}) \\[5pt]
&=&
|\vec{a}|^2 -2\vec{a}\cdot\vec{b}+|\vec{b}|^2 \\[5pt]
&=&
1 -2\cdot 1+3 \\[5pt]
&=&
2
\end{eqnarray}なので、 $\Big| \overrightarrow{ \mathrm{ BA } } \Big|=\sqrt{2}$ です。
同様にして
\begin{eqnarray}
\Big| \overrightarrow{ \mathrm{ BC } } \Big|^2
&=&
(\vec{c}-\vec{b})\cdot (\vec{c}-\vec{b}) \\[5pt]
&=&
|\vec{c}|^2 -2\vec{c}\cdot\vec{b}+|\vec{b}|^2 \\[5pt]
&=&
5 -2\cdot 3+3 \\[5pt]
&=&
2
\end{eqnarray}なので、 $\Big| \overrightarrow{ \mathrm{ BC } } \Big|=\sqrt{2}$ と求められます。
以上から
\begin{eqnarray}
\overrightarrow{ \mathrm{ BA } }\cdot \overrightarrow{ \mathrm{ BC } } &=& \Big| \overrightarrow{ \mathrm{ BA } } \Big|\Big| \overrightarrow{ \mathrm{ BC } } \Big|\cos\angle \mathrm{ ABC } \\[5pt]
-1 &=& \sqrt{2}\cdot\sqrt{2}\cos\angle \mathrm{ ABC } \\[5pt]
\cos\angle \mathrm{ ABC } &=& -\dfrac{1}{2}
\end{eqnarray}なので、 $\angle \mathrm{ ABC }=120^{\circ}$ となります。
解答
オカ:-1
キク:22
ケコサ:120
解答編 つづき
問題
さらに、辺 AD と辺 BC が平行であるから、 $\angle \mathrm{ BAD }=\angle \mathrm{ ADC }=\myBox{シス}^{\circ}$ である。よって、 $\overrightarrow{ \mathrm{ AD } }=\myBox{セ} \overrightarrow{ \mathrm{ BC } }$ であり\[ \overrightarrow{ \mathrm{ OD } }=\vec{a}-\myBox{ソ}\vec{b}+\myBox{タ}\vec{c} \]と表される。また、四角形 ABCD の面積は $\dfrac{\myBox{チ}\sqrt{\myBox{ツ} }}{\myBox{テ} }$ である。
解説
図は次のようになっています。
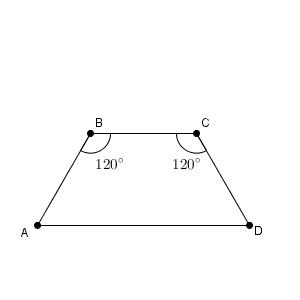
AD と BC が平行で、 $\angle \mathrm{ ABC }=\angle \mathrm{ BCD }=120^{\circ}$ なので、 $\angle \mathrm{ BAD }=\angle \mathrm{ ADC }=60^{\circ}$ となります。
よって、 B, C から AD に垂線を下ろして考えれば、 AD の長さは、 $\mathrm{ AB=CD=BC }=\sqrt{2}$ であることも利用して
\begin{eqnarray}
\sqrt{2}\cdot\frac{1}{2}+\sqrt{2}+\sqrt{2}\cdot\frac{1}{2}=2\sqrt{2}
\end{eqnarray}となります。よって、\[ \overrightarrow{ \mathrm{ AD } }=2\overrightarrow{ \mathrm{ BC } } \]が成り立ちます。
このことから
\begin{eqnarray}
\overrightarrow{ \mathrm{ OD } }
&=&
\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ AD } } \\[5pt]
&=&
\vec{a}+2\overrightarrow{ \mathrm{ BC } } \\[5pt]
&=&
\vec{a}+2(\vec{c}-\vec{b}) \\[5pt]
&=&
\vec{a}-2\vec{b}+2\vec{c} \\[5pt]
\end{eqnarray}となります。
また、四角形 ABCD の面積は、台形の面積なので
\begin{eqnarray}
\dfrac{1}{2} (\sqrt{2}+2\sqrt{2}) \times \frac{\sqrt{6} }{2} = \frac{3\sqrt{3} }{2}
\end{eqnarray}となります。
解答
シス:60
セ:2
ソタ:22
チツテ:332
解答編 つづき
問題
(3) 三角形 OAC を底面とする三角錐 BOAC の体積 $V$ を求めよう。
3点 O, A, C の定める平面 $\alpha$ 上に、点 H を $\overrightarrow{ \mathrm{ BH } }\perp \vec{a}$ と $\overrightarrow{ \mathrm{ BH } }\perp \vec{c}$ が成り立つようにとる。 $\Big|\overrightarrow{ \mathrm{ BH } }\Big|$ は三角錐 BOAC の高さである。 H は $\alpha$ 上の点であるから、実数 s, t を用いて $\overrightarrow{ \mathrm{ OH } }=s\vec{a}+t\vec{c}$ の形に表される。
$\overrightarrow{ \mathrm{ BH } }\cdot{a}=\myBox{ト}$, $\overrightarrow{ \mathrm{ BH } }\cdot{c}=\mybox{ト}$ により、 $s=\myBox{ナ}$, $t=\dfrac{\myBox{ニ} }{\myBox{ヌ} }$ である。よって、 $\Big|\overrightarrow{ \mathrm{ BH } }\Big|=\dfrac{\sqrt{\myBox{ネ} }}{\myBox{ノ} }$ が得られる。したがって、(1)により、 $V=\dfrac{\myBox{ハ} }{\myBox{ヒ} }$ であることがわかる。
解説
$\overrightarrow{ \mathrm{ BH } }$ は $\vec{a}$, $\vec{c}$ と垂直なので、内積は $0$ になります。
$\overrightarrow{ \mathrm{ BH } }\cdot{a}=0$ より
\begin{eqnarray}
(s\vec{a}+t\vec{c}-\vec{b})\cdot \vec{a} &=& 0 \\[5pt]
s+0-1 &=& 0 \\[5pt]
s &=& 1 \\[5pt]
\end{eqnarray}が得られます。また、 $\overrightarrow{ \mathrm{ BH } }\cdot{c}=0$ より
\begin{eqnarray}
(\vec{a}+t\vec{c}-\vec{b})\cdot \vec{c} &=& 0 \\[5pt]
0+5t-3 &=& 0 \\[5pt]
t &=& \frac{3}{5} \\[5pt]
\end{eqnarray}となります。
よって、 $\overrightarrow{ \mathrm{ BH } }=\vec{a}+\dfrac{3}{5}\vec{c}-\vec{b}$ なので
\begin{eqnarray}
\Big| \overrightarrow{ \mathrm{ BH } } \Big|^2
&=&
\left(\vec{a}-\vec{b}+\dfrac{3}{5}\vec{c}\right)\cdot \left(\vec{a}-\vec{b}+\dfrac{3}{5}\vec{c}\right) \\[5pt]
&=&
|\vec{a}|^2+|\vec{b}|^2+\frac{9}{25}|\vec{c}|^2 \\
& &
-2\vec{a}\cdot \vec{b} -\frac{6}{5}\vec{b}\cdot \vec{c}+\frac{6}{5}\vec{a}\cdot \vec{c} \\[5pt]
&=&
1+3+\frac{9}{5}-2 -\frac{18}{5}+0 \\[5pt]
&=&
\frac{1}{5} \\[5pt]
\end{eqnarray}だから、 $\Big| \overrightarrow{ \mathrm{ BH } } \Big|=\dfrac{\sqrt{5} }{5}$ となります。
三角形 OAC の面積は $\dfrac{\sqrt{5} }{2}$ で、高さにあたる BH の長さが $\dfrac{1}{\sqrt{5} }$ なので、三角錐 BOAC の体積 $V$ は
\begin{eqnarray}
\frac{1}{3}\cdot\frac{\sqrt{5} }{2} \cdot \frac{1}{\sqrt{5} } = \frac{1}{6}
\end{eqnarray}となります。
解答
ト:0
ナニヌ:135
ネノ:55
ハヒ:16
解答編 つづき
問題
(4) (3)の $V$ を用いると、四角錐 OABCD の体積は $\myBox{フ}V$ と表せる。さらに、四角形 ABCD を底面とする四角錐 OABCD の高さは $\dfrac{\sqrt{\myBox{ヘ} }}{\myBox{ホ} }$ である。
解説
三角錐 BOAC も四角錐 OABCD も、 A, B, C, D を含む平面を底面と考えれば高さは同じです。なので、体積の比は、底面積の比となります。
三角形 ABC の面積は\[ \frac{1}{2}\cdot \sqrt{2}\cdot \sqrt{2}\sin 120^{\circ}=\frac{\sqrt{3} }{2} \]であり、四角形 ABCD の面積は、(2)で求めた通り $\dfrac{3\sqrt{3} }{2}$ なので、四角錐 OABCD の体積は、三角錐 BOAC の体積の3倍なので、 $3V$ となります。
これより、四角形 ABCD を底面としたときの四角錐 OABCD の高さは
\begin{eqnarray}
& &
3V\div \left(\frac{1}{3} \times \frac{3\sqrt{3} }{2}\right) \\[5pt]
&=&
3\cdot \frac{1}{6} \times \frac{2}{\sqrt{3} } \\[5pt]
&=&
\frac{1}{\sqrt{3} } \\[5pt]
&=&
\frac{\sqrt{3} }{3} \\[5pt]
\end{eqnarray}となります。
解答
フヘホ:333





