センター試験 数学II・数学B 2015年度 第2問 解説

問題編

問題

(1) 関数 $f(x)=\dfrac{1}{2}x^2$ の $x=a$ における微分係数 $f'(a)$ を求めよう。h が $0$ でないとき、x が $a$ から $a+h$ まで変化するときの $f(x)$ の平均変化率は $\myBox{ア}+\dfrac{h}{\myBox{イ}}$ である。したがって、求める微分係数は\[ f'(a) = \lim_{h\to \myBox{ウ}}\left( \mybox{ア}+\frac{h}{\mybox{イ}} \right) = \myBox{エ} \]である。

(2) 放物線 $y=\dfrac{1}{2}x^2$ を $C$ とし、$C$ 上に点 $\mathrm{ P }\left( a,\ \dfrac{1}{2}a^2 \right)$ をとる。ただし、$a\gt 0$ とする。点P における C の接線 $\ell$ の方程式は\[ y=\myBox{オ}x -\frac{1}{\myBox{カ}}a^2 \]である。直線 $\ell$ と $x$軸との交点Q の座標は$\left( \dfrac{\myBox{キ}}{\myBox{ク}}, 0 \right)$ である。点Q を通り $\ell$ に垂直な直線を $m$ とすると、$m$ の方程式は\[ y=\frac{\myBox{ケコ}}{\myBox{サ}}x +\frac{\myBox{シ}}{\myBox{ス}} \]である。

　直線m と $x$軸との交点をAとする。三角形APQ の面積を S とおくと\[ S=\frac{a(a^2+\myBox{セ})}{\myBox{ソ}} \]となる。また、$y$軸と線分AP および曲線C によって囲まれた図形の面積を T とおくと\[ T=\frac{a(a^2+\myBox{タ})}{\myBox{チツ}} \]となる。

　$a \gt 0$ の範囲における $S-T$ の値について調べよう。\[ S-T = \frac{a(a^2-\myBox{テ})}{\myBox{トナ}} \]である。$a\gt 0$ であるから、$S-T \gt 0$ となるようなa のとり得る値の範囲は $a \gt \sqrt{\myBox{ニ}}$ である。また、$a \gt 0$ のときの $S-T$ の増減を調べると、$S-T$ は $a=\myBox{ヌ}$ で最小値 $\dfrac{\myBox{ネノ}}{\myBox{ハヒ}}$ をとることがわかる。

考え方

(1)は、微分を定義に沿って求める問題ですね。微分の定義は基本ですが、定義にさかのぼって計算することは少ないので、こう聞かれると答えられない人はいるかもしれません。教科書のはじめの方に載っているはずですが、覚えてないと答えるのは難しいかもしれません。

(2)では、三角形APQ の面積S は、図形的に考えて求めます。積分を使わなくても求められます。T は直線AP の方程式を求めて積分する方法がオーソドックスだと思います。しかし、図形的に考えれば、計算量を減らしながら計算することができます。

計算量が多くなりがちなので、工夫をしないと時間がなくなってしまいます。

解答編

問題

(1) 関数 $f(x)=\dfrac{1}{2}x^2$ の $x=a$ における微分係数 $f'(a)$ を求めよう。h が $0$ でないとき、x が $a$ から $a+h$ まで変化するときの $f(x)$ の平均変化率は $\myBox{ア}+\dfrac{h}{\myBox{イ}}$ である。

解説

平均変化率は、$f(x)$ の変化幅を $x$ の変化幅で割れば出てきます。$f(x)$ の変化幅は、
\begin{eqnarray} f(a+h)-f(a) &=& \frac{(a+h)^2}{2}-\frac{a^2}{2} \\[5pt] &=& ah+\frac{h^2}{2} \end{eqnarray}なので、平均変化率は次のようになります。 \begin{eqnarray} \frac{f(a+h)-f(a)}{h} &=& \frac{ ah+\frac{h^2}{2} }{h} \\[5pt] &=& a+\frac{h}{2} \end{eqnarray}

解答

アイ：a2

解答編 つづき

問題

したがって、求める微分係数は\[ f'(a) = \lim_{h\to \myBox{ウ}}\left( \mybox{ア}+\frac{h}{\mybox{イ}} \right) = \myBox{エ} \]である。

解説

微分の定義ですね。これは覚えていないと答えられないかもしれません。微分とは、変化幅を $0$ に近づけたときの平均変化率の極限です。よって、次のようになります。
\begin{eqnarray} f'(a) &=& \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \\[5pt] &=& \lim_{h \rightarrow 0} \left( a+\frac{h}{2} \right) \\[5pt] &=& a \end{eqnarray}

解答

ウエ：0a

解答編 つづき

問題

(2) 放物線 $y=\dfrac{1}{2}x^2$ を $C$ とし、$C$ 上に点 $\mathrm{ P }\left( a,\ \dfrac{1}{2}a^2 \right)$ をとる。ただし、$a\gt 0$ とする。点P における C の接線 $\ell$ の方程式は\[ y=\myBox{オ}x -\frac{1}{\myBox{カ}}a^2 \]である。

解説

(1)の結果の通り、$f'(a)=a$ なので、この直線の傾きは a です。なので、直線 $\ell$ の方程式は次のように求められます。
\begin{eqnarray} y &=& a(x-a) + \frac{1}{2}a^2 \\[5pt] &=& ax -\frac{1}{2}a^2 \end{eqnarray}

解答

オカ：a2

解答編 つづき

問題

直線 $\ell$ と $x$軸との交点Q の座標は$\left( \dfrac{\myBox{キ}}{\myBox{ク}}, 0 \right)$ である。

解説

解答

解答編 つづき

問題

点Q を通り $\ell$ に垂直な直線を $m$ とすると、$m$ の方程式は\[ y=\frac{\myBox{ケコ}}{\myBox{サ}}x +\frac{\myBox{シ}}{\myBox{ス}} \]である。

解説

直線 $\ell$ の傾きが $a$ なので、これと直交する直線$m$ の傾きは、$-\dfrac{1}{a}$ となります。点Q の座標が $\left( \dfrac{a}{2}, 0 \right)$ なので、直線$m$ の方程式は
\begin{eqnarray} y &=& -\frac{1}{a} \left( x -\frac{a}{2} \right) \\[5pt] &=& -\frac{1}{a}x +\frac{1}{2} \end{eqnarray}となります。

解答

ケコサシス：-1a12

解答編 つづき

問題

　直線m と $x$軸との交点をAとする。三角形APQ の面積を S とおくと\[ S=\frac{a(a^2+\myBox{セ})}{\myBox{ソ}} \]となる。

解説

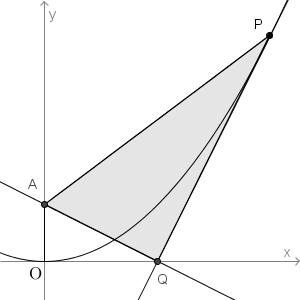
今まで求めたものもまとめると、点P の座標は $\left( a,\dfrac{1}{2}a^2\right)$、点Q の座標は $\left( \dfrac{a}{2}, 0 \right)$ です。また、直線PQ の方程式が $y= ax -\dfrac{a^2}{2}$、直線AQ の方程式が $y=-\dfrac{1}{a}x +\dfrac{1}{2}$ です。このことから、点A の座標が $\left( 0,\dfrac{1}{2}\right)$ であることもわかります。

さて、上の図の色のついた部分の面積を求めます。直線PQ と AQ が直交しているので、$\dfrac{1}{2}\mathrm{ AQ } \cdot \mathrm{ PQ }$ とやりたくなりますが、ルートの計算が出てくるのでめんどくさそうです。ここでは、次のように、台形から引き算をして求める、とやってみます。

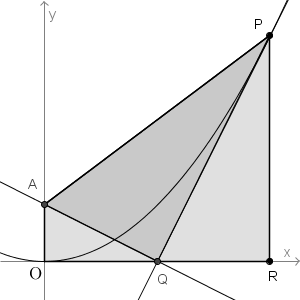
点P から $x$軸に垂線をおろし、交点を R とします。面積S は、台形から三角形OAQ と三角形PQR の面積を引けば求めることができます。台形の面積は、\[\dfrac{1}{2}\cdot \left( \dfrac{1}{2} + \dfrac{1}{2}a^2 \right)\cdot a=\dfrac{a^3+a}{4} \]なので、求める面積S は
\begin{eqnarray} S&=& \frac{a^3+a}{4} -\frac{1}{2}\cdot \frac{a}{2}\cdot \frac{1}{2} -\frac{1}{2}\cdot \left( a -\frac{a}{2} \right)\cdot \frac{1}{2}a^2 \\[5pt] &=& \frac{a^3+a}{4} -\frac{a}{8} -\frac{a^3}{8} \\[5pt] &=& \frac{a^3+a}{8} = \frac{a(a^2+1)}{8} \end{eqnarray}となります。

なお、別解も書いておきます。

まず、$\dfrac{1}{2}\mathrm{ AQ } \cdot \mathrm{ PQ }$ と計算する場合。三平方の定理を使うと、
\begin{eqnarray} & & \frac{1}{2}\sqrt{\left(\frac{1}{2}\right)^2 + \left(\frac{a}{2}\right)^2} \sqrt{\left(\frac{a^2}{2}\right)^2 + \left(\frac{a}{2}\right)^2} \\[5pt] &=& \frac{1}{2} \cdot \frac{\sqrt{a^2+1} }{2} \cdot \frac{a\sqrt{a^2+1} }{2} \\[5pt] &=& \frac{a(a^2+1)}{8} \end{eqnarray}となります。今回はルートがうまく外れるので、それほど複雑な計算にはなりませんね。

また、OQ と QR が同じ長さになることに注意すると、もう少し簡単に計算することができます（が、汎用性のある求め方ではないです）。AP の中点の座標を B とすると、座標は$\left(\dfrac{a}{2},\dfrac{a^2+1}{4}\right)$ となります。求める三角形の面積は、三角形ABQ と PBQ の面積の和なので、
\begin{eqnarray} & & \frac{1}{2} \cdot \frac{a^2+1}{4} \cdot \frac{a}{2} + \frac{1}{2} \cdot \frac{a^2+1}{4} \cdot \frac{a}{2} \\[5pt] &=& \frac{a(a^2+1)}{8} \end{eqnarray}と出すことができます。これだとほとんど計算は不要ですが、今のような特殊なケースでしか適用することができません。

解答

解答編 つづき

問題

また、$y$軸と線分AP および曲線C によって囲まれた図形の面積を T とおくと\[ T=\frac{a(a^2+\myBox{タ})}{\myBox{チツ}} \]となる。

解説

面積T を直接求めるには、AP の式を出し、それと $\dfrac{1}{2}x^2$ との差を積分する必要があります。しかし、これも台形から引く方針で計算すると少し楽になります。つまり、台形OAPR から、放物線C と OR とPR で囲まれた部分を引けばいいわけです。

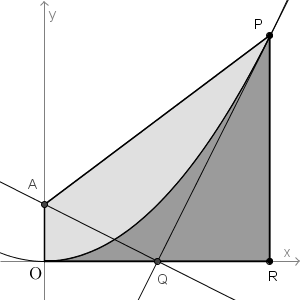
台形の面積は$\dfrac{1}{4}(a^3+a)$なので、
\begin{eqnarray} T &=& \frac{a^3+a}{4} -\int_0^a \frac{x^2}{2} dx \\[5pt] &=& \frac{a^3+a}{4} -\left[ \frac{x^3}{6} \right]_0^a \\[5pt] &=& \frac{a^3+a}{4} -\frac{a^3}{6} \\[5pt] &=& \frac{a^3+3a}{12} \\[5pt] &=& \frac{a(a^2 + 3)}{12} \end{eqnarray}となります。

解答

タチツ：312

解答編 つづき

問題

　$a \gt 0$ の範囲における $S-T$ の値について調べよう。\[ S-T = \frac{a(a^2-\myBox{テ})}{\myBox{トナ}} \]である。$a\gt 0$ であるから、$S-T \gt 0$ となるようなa のとり得る値の範囲は $a \gt \sqrt{\myBox{ニ}}$ である。

解説

S と T は今までで求めた通りなので、
\begin{eqnarray} S-T &=& \frac{a(a^2+1)}{8} - \frac{a(a^2 + 3)}{12} \\[5pt] &=& \frac{(3a^3+3a) -(2a^3+6a)}{24} \\[5pt] &=& \frac{a^3-3a}{24} \\[5pt] &=& \frac{a(a^2-3)}{24} \\[5pt] \end{eqnarray}となります。

$a\gt 0$ なので、$S-T \gt 0$ となるのは、$a^2-3 \gt 0$ とき、つまり、$a \gt \sqrt{3}$ のとき、となります。

解答

テトナ：324
ニ：3

解答編 つづき

問題

また、$a \gt 0$ のときの $S-T$ の増減を調べると、$S-T$ は $a=\myBox{ヌ}$ で最小値 $\dfrac{\myBox{ネノ}}{\myBox{ハヒ}}$ をとることがわかる。

解説

先ほど計算した通り、$S-T=\dfrac{1}{24}a(a^2-3)$ です。右辺を $g(a)$ と置きます。

まずは、$g'(a)=0$ となる a を求めます。
\begin{eqnarray} \frac{3a^2-3}{24} &=& 0 \\ a &=& \pm 1 \end{eqnarray}$a\gt 0$ なので、$a=1$ となります。増減表は次のようになります。 \begin{array}{c|ccccc} a & 0 & \cdots & 1 & \cdots & \\ \hline g'(a) & & - & 0 & + & \\ \hline g(a) & & \searrow & & \nearrow & \end{array}よって、$a=1$ のとき最小となります。このときの $g(a)$ は、$\dfrac{1(1^2-3)}{24}=-\dfrac{1}{12}$ となります。

解答

ヌ：1
ネノハヒ：-112