センター試験 数学II・数学B 2015年度 第4問 解説
問題編
問題
1辺の長さが $1$ のひし形OABC において、$\angle \mathrm{ AOC }=120^{\circ}$とする。辺AB を $2:1$ に内分する点を P とし、直線BC 上に点Q を $\overrightarrow{ \mathrm{ OP } }\perp \overrightarrow{ \mathrm{ OQ } }$ となるようにとる。以下、$\overrightarrow{ \mathrm{ OA } }=\vec{ a }$、$\overrightarrow{ \mathrm{ OB } }=\vec{ b }$ とおく。
(1) 三角形OPQ の面積を求めよう。$\overrightarrow{ \mathrm{ OP } }=\dfrac{\myBox{ア}}{\myBox{イ}}\vec{ a }+\dfrac{\myBox{ウ}}{\mybox{イ}}\vec{ b }$ である。実数t を用いて $\overrightarrow{ \mathrm{ OQ } }=(1-t)\overrightarrow{ \mathrm{ OB } }+t\overrightarrow{ \mathrm{ OC } }$ と表されるので、$\overrightarrow{ \mathrm{ OQ } }=\myBox{エ}\ t\vec{ a }+\vec{ b }$ である。ここで、$\vec{ a }\cdot\vec{ b }=\dfrac{\myBox{オ}}{\myBox{カ}}$、$\overrightarrow{ \mathrm{ OP } }\cdot\overrightarrow{ \mathrm{ OQ } }=\myBox{キ}$ であることから、$t=\dfrac{\myBox{ク}}{\myBox{ケ}}$ である。
これらのことから、$|\overrightarrow{ \mathrm{ OP } }|=\dfrac{\sqrt{\myBox{コ}} }{\myBox{サ}}$、$|\overrightarrow{ \mathrm{ OQ } }| = \dfrac{\sqrt{\myBox{シス}} }{\myBox{セ}}$ である。よって、三角形OPQ の面積$S_1$ は、$S_1 = \dfrac{\myBox{ソ}\sqrt{\myBox{タ}} }{\myBox{チツ}}$ である。
(2) 辺BC を $1:3$ に内分する点を R とし、直線OR と直線PQ との交点を T とする。$\overrightarrow{ \mathrm{ OT } }$ を $\vec{ a }$ と $\vec{ b }$ を用いて表し、三角形OPQ と三角形PRT の面積比を求めよう。
T は直線OR上の点であり、直線PQ上の点でもあるので、実数r、s を用いて\[ \overrightarrow{ \mathrm{ OT } } = r\overrightarrow{ \mathrm{ OR } } = (1-s)\overrightarrow{ \mathrm{ OP } } + s\overrightarrow{ \mathrm{ OQ } } \]と表すと、$r=\dfrac{\myBox{テ}}{\myBox{ト}}$、$s=\dfrac{\myBox{ナ}}{\myBox{ニ}}$ となることがわかる。よって、$\overrightarrow{ \mathrm{ OT } } = \dfrac{\myBox{ヌネ}}{\myBox{ノハ}}\vec{ a } + \dfrac{\myBox{ヒ}}{\myBox{フ}}\vec{ b } $である。
上で求めた r、s の値から、三角形OPQ の面積$S_1$ と、三角形PRT の面積$S_2$ との比は、$S_1:S_2=\myBox{ヘホ}:2$ である。
考え方
(1)の前半では、$\overrightarrow{ \mathrm{ OP } }$ と $\overrightarrow{ \mathrm{ OQ } }$ との内積が 0 になることを用いて係数を決定していきます。後半の三角形の面積は、直角三角形であることを考えれば簡単に出せます。
(2)の前半では、ベクトルを2通りで表して係数を決める、という典型的な問題です。後半は、面積の比を出すだけなので、面積を求める必要はありません。ベクトルの表現から辺の比を考えていくと、2つの三角形の面積比が出てきます。
解答編
問題
1辺の長さが $1$ のひし形OABC において、$\angle \mathrm{ AOC }=120^{\circ}$とする。辺AB を $2:1$ に内分する点を P とし、直線BC 上に点Q を $\overrightarrow{ \mathrm{ OP } }\perp \overrightarrow{ \mathrm{ OQ } }$ となるようにとる。以下、$\overrightarrow{ \mathrm{ OA } }=\vec{ a }$、$\overrightarrow{ \mathrm{ OB } }=\vec{ b }$ とおく。
(1) 三角形OPQ の面積を求めよう。$\overrightarrow{ \mathrm{ OP } }=\dfrac{\myBox{ア}}{\myBox{イ}}\vec{ a }+\dfrac{\myBox{ウ}}{\mybox{イ}}\vec{ b }$ である。実数t を用いて $\overrightarrow{ \mathrm{ OQ } }=(1-t)\overrightarrow{ \mathrm{ OB } }+t\overrightarrow{ \mathrm{ OC } }$ と表されるので、$\overrightarrow{ \mathrm{ OQ } }=\myBox{エ}\ t\vec{ a }+\vec{ b }$ である。
解説
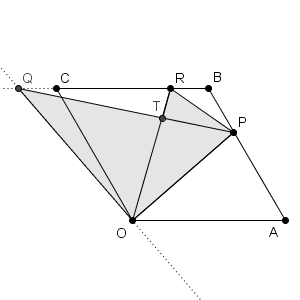
図は、次のようになっています。

点P は辺AB を $2:1$ に内分する点なので、$\overrightarrow{\mathrm{ OP } }= \dfrac{1}{3} \overrightarrow{a} + \dfrac{2}{3} \overrightarrow{b}$ となります。
また、$\overrightarrow{\mathrm{ OQ } }$ は次のように求められます。
\begin{eqnarray}
\overrightarrow{\mathrm{ OQ } } &=& (1-t) \overrightarrow{\mathrm{ OB } } + t \overrightarrow{\mathrm{ OC } } \\
&=& (1-t) \overrightarrow{b} + t ( -\overrightarrow{a}+\overrightarrow{b} ) \\
&=& -t \overrightarrow{a} + \overrightarrow{b}
\end{eqnarray}
解答
アイウ:132エ:-
解答編 つづき
問題
ここで、$\vec{ a }\cdot\vec{ b }=\dfrac{\myBox{オ}}{\myBox{カ}}$、$\overrightarrow{ \mathrm{ OP } }\cdot\overrightarrow{ \mathrm{ OQ } }=\myBox{キ}$ であることから、$t=\dfrac{\myBox{ク}}{\myBox{ケ}}$ である。
解説
ひし形OABC について、$\angle\mathrm{ AOC }=120^{\circ}$ なので、三角形OAB は正三角形です。よって、
\begin{eqnarray}
\vec{a} \cdot \vec{ b }
&=&
\mathrm{ OA } \cdot \mathrm{ OB } \cos \angle \mathrm{ BOA } \\
&=&
1 \cdot 1 \cos 60^{\circ} = \frac{1}{2}
\end{eqnarray}となります。
また、Q は OP と OQ が垂直になるようにとったことから、$\overrightarrow{\mathrm{ OP } } \cdot \overrightarrow{\mathrm{ OQ } }=0$ です。
$\overrightarrow{\mathrm{ OP } } \cdot \overrightarrow{\mathrm{ OQ } }$ を $\vec{a}$と$\vec{b}$ を使って表すと、
\begin{eqnarray}
\overrightarrow{\mathrm{ OP } } \cdot \overrightarrow{\mathrm{ OQ } }
&=&
\left( \frac{1}{3} \overrightarrow{a} + \frac{2}{3} \overrightarrow{b} \right) \cdot (-t \overrightarrow{a} + \overrightarrow{b}) \\[5pt]
&=&
-\frac{t}{3} | \overrightarrow{a} |^2 + \left( \frac{1}{3} - \frac{2}{3}t \right) \overrightarrow{a} \cdot \overrightarrow{b} + \frac{2}{3} |\overrightarrow{b}|^2 \\[5pt]
&=&
-\frac{t}{3}+ \left( \frac{1}{3} - \frac{2}{3}t \right) \cdot \frac{1}{2} + \frac{2}{3} \\[5pt]
&=&
\frac{ -2t + 1 -2t +4 }{ 6 } \\[5pt]
&=&
\frac{ -4t + 5 }{ 6 }
\end{eqnarray}となります。
これが 0 になるので、$-4t+5=0$ から $t=\dfrac{5}{4}$ となります。
解答
オカ:12キ:0
クケ:54
解答編 つづき
問題
これらのことから、$|\overrightarrow{ \mathrm{ OP } }|=\dfrac{\sqrt{\myBox{コ}} }{\myBox{サ}}$、$|\overrightarrow{ \mathrm{ OQ } }| = \dfrac{\sqrt{\myBox{シス}} }{\myBox{セ}}$ である。よって、三角形OPQ の面積$S_1$ は、$S_1 = \dfrac{\myBox{ソ}\sqrt{\myBox{タ}} }{\myBox{チツ}}$ である。
解説
OP の長さは、\begin{eqnarray} | \overrightarrow{\mathrm{ OP } } | ^2 &=& \left| \frac{1}{3} \vec{a} + \frac{2}{3} \vec{b} \right| ^2 \\[5pt] &=& \frac{1}{9}| \vec{a} |^2 + \frac{4}{9} \vec{a} \cdot \vec{b} + \frac{4}{9} |\vec{b}|^2 \\[5pt] &=& \frac{1}{9} + \frac{4}{9} \cdot \frac{1}{2} + \frac{4}{9} \\[5pt] &=& \frac{7}{9} \end{eqnarray}から、$\dfrac{\sqrt{7}}{3}$ とわかります。
OQ については、上で求めた $t=\dfrac{5}{4}$ を使って、
\begin{eqnarray}
| \overrightarrow{\mathrm{ OQ } } | ^2
&=&
\left| -\frac{5}{4} \vec{a} + \vec{b} \right| ^2 \\[5pt]
&=&
\frac{25}{16}| \vec{a} |^2 - \frac{5}{2} \vec{a} \cdot \vec{b} + |\vec{b}|^2 \\[5pt]
&=&
\frac{25}{16} - \frac{5}{2} \cdot \frac{1}{2} + 1 \\[5pt]
&=&
\frac{21}{16}
\end{eqnarray}となるので、OQの長さは $\dfrac{\sqrt{21} }{4}$ とわかります。
よって、三角形OPQ の面積$S_1$ は、$\angle\mathrm{ POQ }=90^{\circ}$ であることに注意すると、
\begin{eqnarray}
S_1
&=&
\frac{1}{2} \mathrm{ OP }\cdot \mathrm{ OQ } \\
&=&
\frac{1}{2} \cdot \frac{\sqrt{7} }{3} \cdot \frac{\sqrt{21} }{4} \\[5pt]
&=&
\frac{7\sqrt{3} }{24}
\end{eqnarray}と求められます。
解答
コサ:73シスセ:214
ソタチツ:7324
解答編 つづき
問題
(2) 辺BC を $1:3$ に内分する点を R とし、直線OR と直線PQ との交点を T とする。$\overrightarrow{ \mathrm{ OT } }$ を $\vec{ a }$ と $\vec{ b }$ を用いて表し、三角形OPQ と三角形PRT の面積比を求めよう。
T は直線OR上の点であり、直線PQ上の点でもあるので、実数r、s を用いて\[ \overrightarrow{ \mathrm{ OT } } = r\overrightarrow{ \mathrm{ OR } } = (1-s)\overrightarrow{ \mathrm{ OP } } + s\overrightarrow{ \mathrm{ OQ } } \]と表すと、$r=\dfrac{\myBox{テ}}{\myBox{ト}}$、$s=\dfrac{\myBox{ナ}}{\myBox{ニ}}$ となることがわかる。よって、$\overrightarrow{ \mathrm{ OT } } = \dfrac{\myBox{ヌネ}}{\myBox{ノハ}}\vec{ a } + \dfrac{\myBox{ヒ}}{\myBox{フ}}\vec{ b } $である。
解説
図は次のようになっています。
これらの係数を比較すると、
\begin{eqnarray}
\left\{
\begin{array}{1}
\displaystyle -\frac{1}{4}r = \frac{4-19s}{12} \\[5pt]
\displaystyle r = \frac{2+s}{3}
\end{array}
\right.
\end{eqnarray}
という連立方程式ができます。2つ目の式を1つ目に代入すると、
\begin{eqnarray}
-\frac{1}{4} \cdot \frac{2+s}{3} &=& \frac{4-19s}{12} \\[5pt]
-2-s &=& 4-19s \\
18s &=& 6 \\
s &=& \frac{1}{3} \\
\end{eqnarray}
となります。これを連立方程式の2つ目に代入すると
\begin{eqnarray}
r &=& \frac{2+\frac{1}{3} }{3}
&=& \frac{6+1}{9}
&=& \frac{7}{9}
\end{eqnarray}となります。
r を用いた $\overrightarrow{\mathrm{ OT } }$ の式に代入すると
\begin{eqnarray}
\overrightarrow{\mathrm{ OT } }
&=&
-\frac{1}{4}r \vec{a} + r \vec{b} \\[5pt]
&=&
-\frac{1}{4}\cdot \frac{7}{9} \vec{a} + \frac{7}{9} \vec{b} \\[5pt]
&=&
-\frac{7}{36} \vec{a} + \frac{7}{9} \vec{b}
\end{eqnarray}と求められます。
解答
テトナニ:7913ヌネノハ:-736
ヒフ:79
解答編 つづき
問題
上で求めた r、s の値から、三角形OPQ の面積$S_1$ と、三角形PRT の面積$S_2$ との比は、$S_1:S_2=\myBox{ヘホ}:2$ である。
解説
三角形OPQ の面積$S_1$ と三角形PRT の面積$S_2$ の比を求めます。比を求めるだけでいいので、$S_2$ を直接計算する必要はありません。三角形OPQ と三角形PRT の2つを考える前に、三角形PQR を考えてみましょう。
三角形OPQ と三角形PQR について、PQ が共通しているので、面積の比は OT と TR の比と一致します。そしてこの比は、\[ r:1-r=\frac{7}{9}:\frac{2}{9}=7:2 \]と書けます。
また、三角形PQR と三角形PRT については、PR が共通しているので、面積の比は PQ と PR の比に一致し、\[ 1:s=1:\frac{1}{3}=3:1 \]と書くことができます。
よって、\[ S_2 = \frac{2}{7}\cdot\frac{1}{3}S_1=\frac{2}{21} S_1 \]なので、$S_1:S_2=21:2$ となります。





