センター試験 数学I・数学A 2019年度追試 第2問 [2] 解説
【必答問題】
問題編
問題
疫病Aに関するいくつかのデータについて考える。
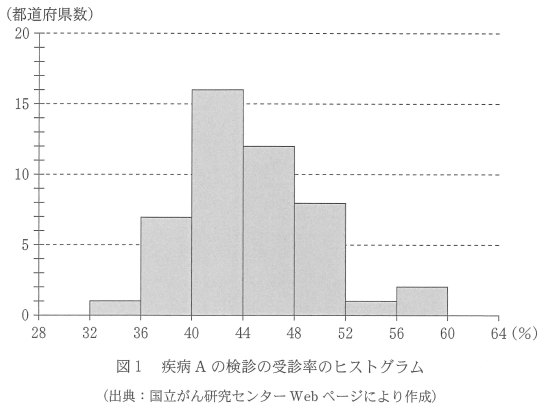
(1) 図1は、47都道府県の40歳以上69歳以下を対象とした「疫病Aの検診の受診率」のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
次の $\mybox{サ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つ選べ。
疫病Aの検診の受診率の中央値として図1のヒストグラムと矛盾しないものは $\myBox{サ}$ である。
0: 16.0
1: 24.0
2: 35.6
3: 43.4
4: 44.7
5: 46.0
(2) 疫病Aの「調整済み死亡数」が毎年、都道府県ごとに算出されている。なお、この調整済み死亡数は年齢構成などを考慮した10万人あたりの死亡数であり、例えば5.3のように小数になることもある。
図2は、各都道府県の疫病Aによる調整済み死亡数 $Y$ を、年ごとに箱ひげ図にして並べたものである。
図2に関する次の記述(I)、(II)、(III)について正誤を判定する。
(I) 1996年から2009年までの間における各年の $Y$ の中央値は、前年より小さくなる年もあるが、この間は全体として増加する傾向にある。
(II) $Y$ の最大値が最も大きい年と $Y$ の最大値は最も小さい年とを比べた場合、これら二つの年における最大値の差は2以下である。
(III) 1996年と2014年で、 $Y$ が9以下の都道府県数を比べると、2014年は1996年の $\dfrac{1}{2}$ 以下である。
次の $\mybox{シ}$ に当てはまるものを、次の 0 ~ 7 のうちから一つ選べ。
(I)、(II)、(III)の記述の正誤について正しい組合せは $\myBox{シ}$ である。
0 1 2 3 (I) 正 正 正 誤 (II) 正 正 誤 正 (III) 正 語 正 正
4 5 6 7 (I) 正 誤 誤 誤 (II) 誤 正 誤 誤 (III) 誤 語 正 誤
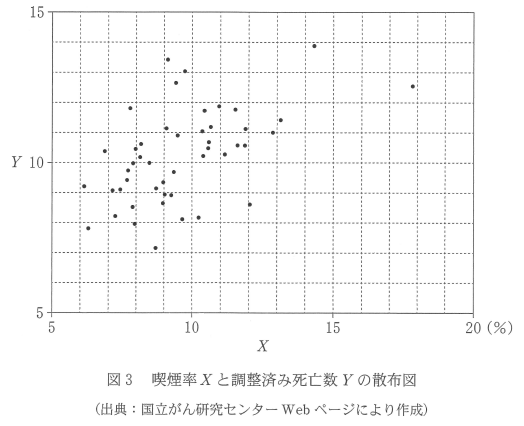
(3) 図3は、ある年の47都道府県の喫煙率 $X$ と同じ年の調整済み死亡数 $Y$ との関係を表している。
次の $\mybox{ス}$ に当てはまるものを、下の⓪ ~ ③ のうちから一つ選べ。
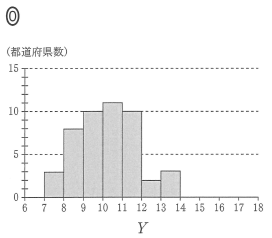
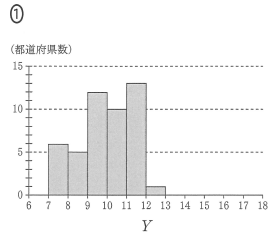
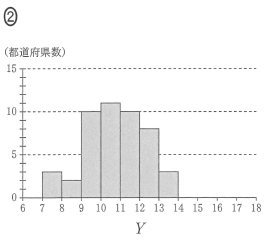
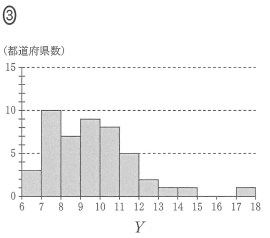
$Y$ のヒストグラムとして最も適切なものは $\myBox{ス}$ である。
(4) 表1は、図3に表されている喫煙率 $X$ と調整済み死亡数 $Y$ の平均値、分散および共分散を計算したものである。ただし、共分散とは「 $X$ の偏差と $Y$ の偏差の積の平均値」である。なお、表1の数値は四捨五入していない正確な値とする。
表1 平均値、分散、共分散 平均値 分 散 共分散 $X$ 9.6 4.8 1.75 $Y$ 10.2 2.4 喫煙率 $X$ のとる値を $x$ 、調整済み死亡数 $Y$ のとる値を $y$ とする。次の $x$ と $y$ の関係式(*) はデータの傾向を知るためによく使われる式である。\[ y-\bar{y}=\frac{s_{XY} }{s_{X}^2}(x-\bar{x}) \quad \cdots (*) \]ここで、 $\bar{x}, \bar{y}$ はそれぞれ $X, Y$ の平均値、 $s_{X}^2$ は $X$ の分散、 $s_{XY}$ は $X$ と $Y$ の共分散を表す。
次の $\mybox{セ}$, $\mybox{ソ}$, $\mybox{タ}$ それぞれに当てはまる数値として最も近いものを下の0 ~ 9のうちから一つずつ選べ。
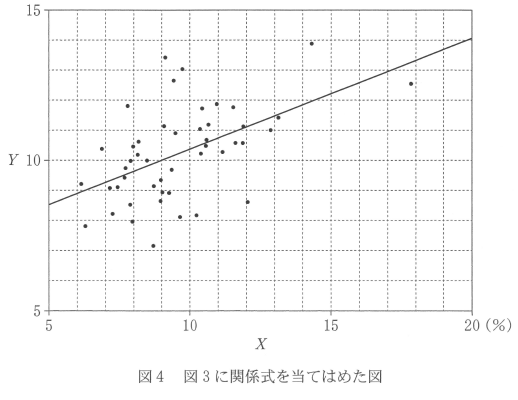
図3の散布図に対する関係式(*)は $y=\myBox{セ}x+\myBox{ソ}$ であり、図4はこの関係式を図3に当てはめたものである。
喫煙率が3%から20%の間では同じ傾向があると考えたとき、上で求めた式を用いると、喫煙率が4%であれば調整済み死亡数は $\myBox{タ}$ である。0: 0.36
1: 0.53
2: 0.80
3: 1.26
4: 2.775: 5.13
6: 6.74
7: 8.18
8: 8.87
9: 9.95
考え方
(1)は、中央値の定義がわかっていれば解けるでしょう。(2)は、箱ひげ図の見方がわかっていれば解けます。どれもあまりひねったものではないです。
(3)は、散布図とヒストグラムの関係を考えますが、これもヒストグラムをどう作るかがわかっていれば難しくはありません。
データの分析は、最後に抽象的で難しい問題が出題されることが多いですが、(4)は、例年ほどは難しくはありません。見慣れない式が出てきますが、各変数が何を表しているか説明されているので、言われた通りに計算するだけです。
【必答問題】
解答編
問題
疫病Aに関するいくつかのデータについて考える。
(1) 図1は、47都道府県の40歳以上69歳以下を対象とした「疫病Aの検診の受診率」のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
次の $\mybox{サ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つ選べ。
疫病Aの検診の受診率の中央値として図1のヒストグラムと矛盾しないものは $\myBox{サ}$ である。
0: 16.0
1: 24.0
2: 35.6
3: 43.4
4: 44.7
5: 46.0
解説
中央値とは、ちょうど真ん中にあたる値のことです。今の場合、値の数は47なので、下から24番目の値が中央値となります。
下から都道府県数を数えていくと、1, 7, 16, 12, 8, 1, 2 なので、上から24番目は、16の部分です。つまり、中央値は、40%以上44%未満の階級に含まれている、ということです。そのため、中央値として矛盾しないものは、選択肢3の43.4となります。
解答
サ:3
参考
解答編 つづき
(2) 疫病Aの「調整済み死亡数」が毎年、都道府県ごとに算出されている。なお、この調整済み死亡数は年齢構成などを考慮した10万人あたりの死亡数であり、例えば5.3のように小数になることもある。
図2は、各都道府県の疫病Aによる調整済み死亡数 $Y$ を、年ごとに箱ひげ図にして並べたものである。
図2に関する次の記述(I)、(II)、(III)について正誤を判定する。
(I) 1996年から2009年までの間における各年の $Y$ の中央値は、前年より小さくなる年もあるが、この間は全体として増加する傾向にある。
(II) $Y$ の最大値が最も大きい年と $Y$ の最大値は最も小さい年とを比べた場合、これら二つの年における最大値の差は2以下である。
(III) 1996年と2014年で、 $Y$ が9以下の都道府県数を比べると、2014年は1996年の $\dfrac{1}{2}$ 以下である。
次の $\mybox{シ}$ に当てはまるものを、次の 0 ~ 7 のうちから一つ選べ。
(I)、(II)、(III)の記述の正誤について正しい組合せは $\myBox{シ}$ である。
0 1 2 3 (I) 正 正 正 誤 (II) 正 正 誤 正 (III) 正 語 正 正
4 5 6 7 (I) 正 誤 誤 誤 (II) 誤 正 誤 誤 (III) 誤 語 正 誤
解説
一つずつ、記述が正しいかどうかを確認していきます。
(I)中央値は、箱ひげ図の真ん中にある太い線のことです。図では、上に進むほど(年代が進むほど)、中央値を表す線は右に来る傾向にあります。そのため、正しいといえます。
(II)最大値は、箱ひげ図の右端の部分のことです。最大値が最も大きいのは、2011年で、値は約15です。最大値が最も小さいのは、1996年で、値は12より少し小さい値です。差は3以上なので、2以下ではありません。そのため、誤りです。
(III)1996年を見ると、中央値が9以下であることから、半数以上が9以下であることがわかります。一方、2014年は、箱の左部分、つまり、25%の部分が9以上なので、25%以下の都道府県で9以下だとわかります。そのため、 $Y$ が9以下の都道府県数を比べると、2014年は1996年の $\dfrac{1}{2}$ 以下だと言えます。正しいです。
以上から、選択肢2が答えだとわかります。
解答
シ:2
参考
解答編 つづき
(3) 図3は、ある年の47都道府県の喫煙率 $X$ と同じ年の調整済み死亡数 $Y$ との関係を表している。
次の $\mybox{ス}$ に当てはまるものを、下の⓪ ~ ③ のうちから一つ選べ。
$Y$ のヒストグラムとして最も適切なものは $\myBox{ス}$ である。
解説
$Y$ のヒストグラムを選ぶので、図3の縦の軸について見ていきます。一番小さな値は、7より少し大きな値ですね。7と8の間には、3つ点があります。このことから、ヒストグラムのうち、選択肢1と3は正しくないことがわかります。
選択肢0と2は、8以上9未満の階級の値が異なるので、この部分を図3を用いて考えてみます。 $Y$ の値が8と9の間にあるのは、8点です。そのため、選択肢2も正しくないことがわかり、選択肢0が最も適切だとわかります。他の階級も、図3とは矛盾しません。
解答
ス:0
解答編 つづき
(4) 表1は、図3に表されている喫煙率 $X$ と調整済み死亡数 $Y$ の平均値、分散および共分散を計算したものである。ただし、共分散とは「 $X$ の偏差と $Y$ の偏差の積の平均値」である。なお、表1の数値は四捨五入していない正確な値とする。
表1 平均値、分散、共分散 平均値 分 散 共分散 $X$ 9.6 4.8 1.75 $Y$ 10.2 2.4 喫煙率 $X$ のとる値を $x$ 、調整済み死亡数 $Y$ のとる値を $y$ とする。次の $x$ と $y$ の関係式(*) はデータの傾向を知るためによく使われる式である。\[ y-\bar{y}=\frac{s_{XY} }{s_{X}^2}(x-\bar{x}) \quad \cdots (*) \]ここで、 $\bar{x}, \bar{y}$ はそれぞれ $X, Y$ の平均値、 $s_{X}^2$ は $X$ の分散、 $s_{XY}$ は $X$ と $Y$ の共分散を表す。
次の $\mybox{セ}$, $\mybox{ソ}$, $\mybox{タ}$ それぞれに当てはまる数値として最も近いものを下の0 ~ 9のうちから一つずつ選べ。
図3の散布図に対する関係式(*)は $y=\myBox{セ}x+\myBox{ソ}$ であり、図4はこの関係式を図3に当てはめたものである。
喫煙率が3%から20%の間では同じ傾向があると考えたとき、上で求めた式を用いると、喫煙率が4%であれば調整済み死亡数は $\myBox{タ}$ である。0: 0.36
1: 0.53
2: 0.80
3: 1.26
4: 2.775: 5.13
6: 6.74
7: 8.18
8: 8.87
9: 9.95
解説
与えられている式に、与えられている値を代入して計算します。\[ y-\bar{y}=\frac{s_{XY} }{s_{X}^2}(x-\bar{x}) \]の式で、 $\bar{x}$, $\bar{y}$ は平均値だから、9.6と10.2をそれぞれ代入します。また、 $s_{XY}$ は共分散なので1.75を代入し、 $s_{X}^2$ は $X$ の分散なので4.8を代入します。
\begin{eqnarray}
y-10.2 &=& \frac{1.75}{4.8}(x-9.6) \\[5pt]
y-10.2 &=& \frac{1.75}{4.8}x-3.5 \\[5pt]
y &=& \frac{175}{480}x-3.5+10.2 \\[5pt]
&=& \frac{35}{96}x+6.7 \\[5pt]
\end{eqnarray}となります。傾きは $\dfrac{35}{96}=0.364\cdots$ なので、一番近いものは選択肢0の0.36です。切片は、6.7なので、一番近いものは選択肢6の6.74です。
同じ傾向があると考えると、喫煙率が4%のときの調整済み死亡数は、この式を用いて計算できます。
\begin{eqnarray}
& & \frac{35}{96}\times 4+6.7
&=& \frac{35}{24}+6.7 \\[5pt]
&=& 8.15\cdots \\[5pt]
\end{eqnarray}となるので、一番近いものは選択肢7の8.18となります。
解答
セソタ:067