センター試験 数学I・数学A 2019年度追試 第2問 [1] 解説
【必答問題】
問題編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ BC }=12$, $\cos\angle \mathrm{ ABC }=\dfrac{1}{3}$, $\cos\angle \mathrm{ ACB }=\dfrac{7}{9}$ とする。このとき
\begin{eqnarray} & & \mathrm{ AB } \cdot \cos\angle \mathrm{ ABC }+\mathrm{ AC }\cdot\cos\angle \mathrm{ ACB }=\myBox{アイ}, \\[5pt] & & \dfrac{\mathrm{ AB } }{\mathrm{ AC } }=\frac{\myBox{ウ} }{\myBox{エ} } \end{eqnarray}である。したがって\[ \mathrm{ AB }=\myBox{オ},\ \mathrm{AC}=\myBox{カキ} \]であり、辺 BC の中点を D とすると $\mathrm{ AD }=\myBox{ク}\sqrt{\myBox{ケコ} }$ である。
考え方
アイの部分は、第一余弦定理と呼ばれるものです。ただ、それを知らなくても、 $\mathrm{ AB } \cdot \cos\angle \mathrm{ ABC }$ などがどの部分を表しているか、図をかけば思いつけるでしょう。
ウエの部分は、ノーヒントだと少し難しいですが、図を用いて何かを2通りで表すという方針で考えるといいでしょう。もしくは、有名な定理を使います。
これができれば、残りはそれほど難しくはないでしょう。「したがって」とあるので、先ほどの2つの式を使って、辺の長さを求めます。 AD は、三角形 ABD で、すでにわかっている辺や角の情報から、何を使うか考えましょう。
【必答問題】
解答編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ BC }=12$, $\cos\angle \mathrm{ ABC }=\dfrac{1}{3}$, $\cos\angle \mathrm{ ACB }=\dfrac{7}{9}$ とする。このとき
\begin{eqnarray} & & \mathrm{ AB } \cdot \cos\angle \mathrm{ ABC }+\mathrm{ AC }\cdot\cos\angle \mathrm{ ACB }=\myBox{アイ}, \\[5pt] & & \dfrac{\mathrm{ AB } }{\mathrm{ AC } }=\frac{\myBox{ウ} }{\myBox{エ} } \end{eqnarray}である。
解説
図をかくと、次のようになります。 A から BC へ下した垂線の足を H としています。
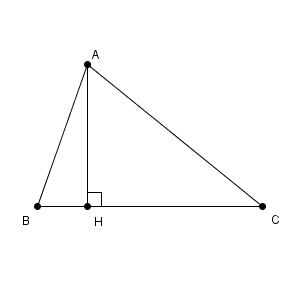
$\angle \mathrm{ ABC }$ も $\angle \mathrm{ ACB }$ も、余弦の値が正なので、鋭角であることがわかります。そのため、上のような図となります。
これより、 $\mathrm{ AB }\cos\angle \mathrm{ ABC }$ は BH と等しく、 $\mathrm{ AC }\cos\angle \mathrm{ ACB }$ は CH と等しいことがわかります。つまり、アイの部分には、 BC の長さ $12$ が入ります。なお、あまり取り上げられることはありませんが、この式は第一余弦定理と呼ばれることもあります。
また、 AB, AC の比率を求めます。直接、長さや長さの比を求めるのは難しいため、何かを2通りで表しましょう。少し思いつきにくいですが、上の図から、 AH を2通りで表してみます。これは、 $\mathrm{ AB }\sin\angle \mathrm{ ABC }$ と書くことも、 $\mathrm{ AC }\sin\angle\mathrm{ ACB }$ と書くこともできます。また、正弦の値は、相互関係から
\begin{eqnarray}
\sin\angle \mathrm{ ABC } &=& \sqrt{1-\left(\frac{1}{3}\right)^2}=\frac{\sqrt{8} }{3} \\[5pt]
\sin\angle \mathrm{ ACB } &=& \sqrt{1-\left(\frac{7}{9}\right)^2}=\frac{\sqrt{32} }{9} \\[5pt]
\end{eqnarray}と求められます。よって、
\begin{eqnarray}
\mathrm{ AB }\sin\angle \mathrm{ ABC }&=&\mathrm{ AC }\sin\angle \mathrm{ ACB } \\[5pt]
\mathrm{ AB }\cdot\frac{\sqrt{8} }{3}&=&\mathrm{ AC }\cdot\frac{\sqrt{32} }{9} \\[5pt]
\frac{\mathrm{ AB } }{\mathrm{ AC } }&=&\frac{\sqrt{32} }{9}\cdot \frac{3}{\sqrt{8} } \\[5pt]
&=&\frac{2}{3} \\[5pt]
\end{eqnarray}となります。もしくは、正弦定理から\[ \frac{\mathrm{ AB } }{\sin\angle \mathrm{ ACB } } = \frac{\mathrm{ AC } }{\sin\angle \mathrm{ ABC } } \]が成り立つので、これを変形しても求められます。ほとんど同じ計算です。
解答
アイ:12
ウエ:23
解答編 つづき
したがって\[ \mathrm{ AB }=\myBox{オ},\ \mathrm{AC}=\myBox{カキ} \]であり、辺 BC の中点を D とすると $\mathrm{ AD }=\myBox{ク}\sqrt{\myBox{ケコ} }$ である。
解説
先ほど求めた式で、2つ目の式を1つ目に代入すると
\begin{eqnarray}
\mathrm{ AB } \cdot \cos\angle \mathrm{ ABC }+\mathrm{ AC }\cdot\cos\angle \mathrm{ ACB }&=&12 \\[5pt]
\frac{2}{3}\mathrm{ AC } \cdot \frac{1}{3}+\mathrm{ AC }\cdot\frac{7}{9}&=&12 \\[5pt]
\left(\frac{2}{9}+\frac{7}{9}\right)\mathrm{ AC }&=&12 \\[5pt]
\mathrm{ AC }&=&12 \\[5pt]
\end{eqnarray}と求められます。よって、\[ \mathrm{ AB }=\frac{2}{3}\cdot 12=8 \]となります。
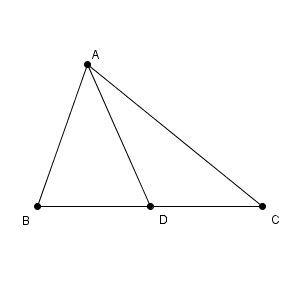
三角形 ABD に対して余弦定理を使うと
\begin{eqnarray}
\mathrm{ AD }^2
&=&
\mathrm{ AB }^2+\mathrm{ BD }^2-2\mathrm{ AB }\cdot\mathrm{ BD }\cdot\cos\angle \mathrm{ ABD } \\[5pt]
&=&
8^2+6^2-2\cdot 8\cdot 6\cdot\frac{1}{3} \\[5pt]
&=&
64+36-32 \\[5pt]
&=&
68 \\[5pt]
\end{eqnarray}となることから、 $\mathrm{ AD }=2\sqrt{17}$ と求められます。
解答
オカキ:812
クケコ:217





