センター試験 数学I・数学A 2017年度追試 第2問 [2] 解説
【必答問題】
問題編
問題
(図は元の問題文を参考に再現しています。)
1組から3組の生徒100人に対し、テストを3回行った。1回目と2回目のテストは100点満点、3回目は200点満点である。
(1) 次の表1および図1は、1回目のテストの組ごとの得点に対する度数分布表および箱ひげ図である。
表1 階級 1組 2組 3組 45点以上50点未満 5 3 4 50点以上55点未満 4 4 2 55点以上60点未満 3 5 10 60点以上65点未満 7 1 7 65点以上70点未満 7 13 4 70点以上75点未満 7 6 5 75点以上80点未満 1 1 1 合計 34 33 33 図1
次の $\mybox{ス}$ に当てはまるものを、下の 0 ~ 5 のうちから一つ選べ。
1組から3組の1回目のテストの結果と対応する図1の箱ひげ図の組合せは $\myBox{ス}$ である。
0 1 2 3 4 5 1組 a a b b c c 2組 b c a c a b 3組 c b c a b a
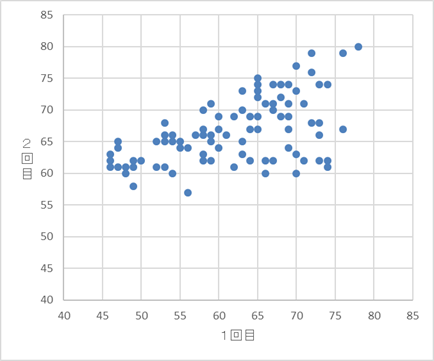
(2) 次の表2は、1回目のテストの得点と2回目のテストの得点の標準偏差と共分散の値であり、図2は、この2つのテストの得点の散布図と箱ひげ図である。ただし、表2の数値は正確な値であり、四捨五入されていないものとする。また、図2の散布図の点は重なっていることもある。
(共分散とは、1回目の得点の偏差と2回目の得点の偏差の積の平均値である。)
表2 標準偏差 共分散 1回目の得点 8.4 25.0 2回目の得点 5.2 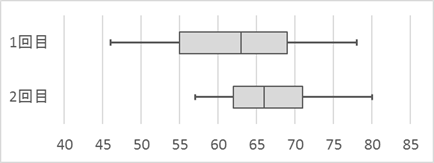
図2 次の $\mybox{セ}, \mybox{ソ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つずつ選べ。ただし、解答の順序は問わない。
表2および図2の散布図と箱ひげ図について述べた文として誤っているものは、 $\myBox{セ}$, $\myBox{ソ}$ である。
0: 四分位範囲は、2回目の得点の方が小さい。
1: 表2から1回目の得点と2回目の得点の相関係数を計算すると、0.65以上になる。
2: 1回目の得点が55点未満であった生徒は全員、1回目の得点より2回目の得点のほうが高い。
3: 2回目の得点が70点以上であった生徒は、25人以上いる。
4: 2回目の得点が1回目の得点より10点以上高い生徒は全員、1回目の得点が55点未満である。
5: 65点以上の得点をとった生徒の人数は、1回目のテストより2回目のテストの方が多い。(3) 次の表3は、1回目のテストの得点と2回目のテストの得点の平均点と標準偏差の値であり、図3は、この2つのテストの得点の散布図である。ただし、表3の数値は正確な値であり、四捨五入されていないものとする。また、図3の散布図の点は重なっていることもある。
表3 平均点 標準偏差 1回目の得点 61.9 8.4 3回目の得点 133.3 26.0 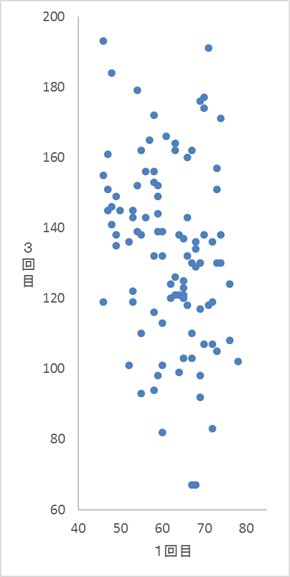
図3 ここで、2つのテストの得点をそれぞれ、次の計算式により新しい得点に換算した。\[ 新しい得点 = 50 + 10 \times \frac{得点の偏差}{標準偏差} \quad \cdots (*) \]
次の $\mybox{タ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
1回目の得点を式 (*) により換算した新しい得点と3回目の得点と式 (*) により換算した新しい得点の散布図は $\myBox{タ}$ である。
01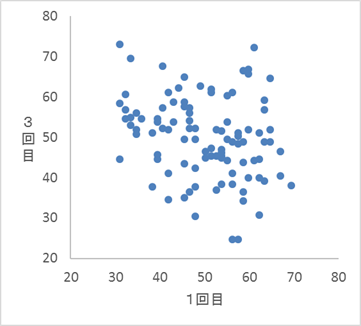 2
2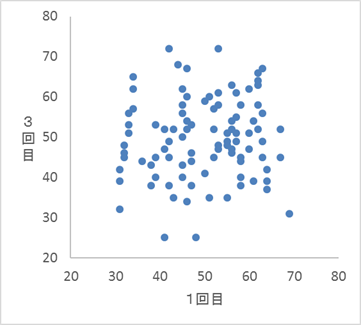 3
3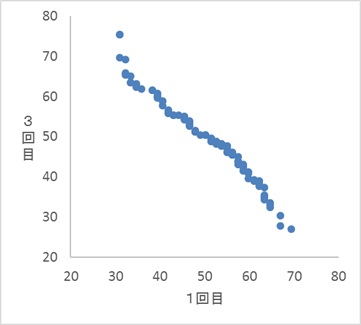
考え方
(1)は、中央値、第1四分位数から考えましょう。
(2)は、散布図と箱ひげ図のどちらを参照するかよく考えましょう。この問題では、散布図上の点は重なっている可能性があるため、散布図は人数を数えるのには向いていません。
(3)は、変換によって、データの大小関係がどうかわるかを考えましょう。
【必答問題】
解答編
問題
(図は元の問題文を参考に再現しています。)
1組から3組の生徒100人に対し、テストを3回行った。1回目と2回目のテストは100点満点、3回目は200点満点である。
(1) 次の表1および図1は、1回目のテストの組ごとの得点に対する度数分布表および箱ひげ図である。
表1 階級 1組 2組 3組 45点以上50点未満 5 3 4 50点以上55点未満 4 4 2 55点以上60点未満 3 5 10 60点以上65点未満 7 1 7 65点以上70点未満 7 13 4 70点以上75点未満 7 6 5 75点以上80点未満 1 1 1 合計 34 33 33 図1
次の $\mybox{ス}$ に当てはまるものを、下の 0 ~ 5 のうちから一つ選べ。
1組から3組の1回目のテストの結果と対応する図1の箱ひげ図の組合せは $\myBox{ス}$ である。
0 1 2 3 4 5 1組 a a b b c c 2組 b c a c a b 3組 c b c a b a
解説
箱ひげ図から、最大値と最小値はすぐにわかりますが、これと表1を照らし合わせても、何もわかりません。なので、中央値や四分位数を見ていく必要があります。
まず、1組は34人なので、中央値は17番目と18番目の平均です。表1を使うと、ともに「60点以上65点未満」の階級に属するので、中央値もこの値になります。また第1四分位数は、下位17人の中央値なので、下から9番目の値です。なので、「50点以上55点未満」の階級です。第3四分位数は、上位17人の中央値なので、上から9番目だから「65点以上70点未満」です。これらをすべて満たすものは、 b しかありません。第1四分位数からしぼることができます。
次に、2組を考えましょう。33人なので、中央値は、上から17番目です。「65点以上70点未満」です。これを満たすのは、 c しかありません。
最後に、念のため3組も考えましょう。これも33人なので、上から17番目を見ればいいので、中央値は「60点以上65点未満」です。また、第1四分位数は、下位16人の中央値なので、下から8番目と9番目の平均です。ともに「55点以上60点未満」の階級に属するので、第1四分位数もここに属します。第3四分位数は、上位8番目と9番目の平均なので、「65点以上70点未満」となり、第3四分位数もここに属します。これをすべて満たすのは、 a しかありません。中央値と第1四分位数からしぼれます。
解答
ス:3
参考
解答編 つづき
問題
(2) 次の表2は、1回目のテストの得点と2回目のテストの得点の標準偏差と共分散の値であり、図2は、この2つのテストの得点の散布図と箱ひげ図である。ただし、表2の数値は正確な値であり、四捨五入されていないものとする。また、図2の散布図の点は重なっていることもある。
(共分散とは、1回目の得点の偏差と2回目の得点の偏差の積の平均値である。)
表2 標準偏差 共分散 1回目の得点 8.4 25.0 2回目の得点 5.2 
図2 次の $\mybox{セ}, \mybox{ソ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つずつ選べ。ただし、解答の順序は問わない。
表2および図2の散布図と箱ひげ図について述べた文として誤っているものは、 $\myBox{セ}$, $\myBox{ソ}$ である。
0: 四分位範囲は、2回目の得点の方が小さい。
1: 表2から1回目の得点と2回目の得点の相関係数を計算すると、0.65以上になる。
2: 1回目の得点が55点未満であった生徒は全員、1回目の得点より2回目の得点のほうが高い。
3: 2回目の得点が70点以上であった生徒は、25人以上いる。
4: 2回目の得点が1回目の得点より10点以上高い生徒は全員、1回目の得点が55点未満である。
5: 65点以上の得点をとった生徒の人数は、1回目のテストより2回目のテストの方が多い。
解説
1つ1つ見ていきます。
0に出てくる「四分位範囲」とは、第3四分位数と第1四分位数との差のことで、簡単に言うと箱ひげ図の箱の長さです。2回目の方が箱が短くなっているので、これは正しい文です。
1に出てくる「相関係数」とは、共分散をそれぞれの標準偏差で割ったものです。計算すると\[ 25.0 \div (8.4 \times 5.2) = 0.572\cdots \]となるので、0.65以上にはなりません。誤っている文です。
2は、散布図を見ましょう「1回目が55点」の部分より左にある点は、すべて、2回目は55点以上です。2回目の方が得点が高くなっています。よって正しい文です。
3は、箱ひげ図を見ましょう。2回目の第3四分位数が70より大きいですね。第3四分位数はざっくりいうと上位25%の値なので、70点以上の生徒が25人以上いると言えます。正しい文です。
なお、3は、散布図を使って、70点以上の点の数を数えてもわかりますが、いい方法ではありません。めんどくさいというのもありますが、問題文の注意書きにもあるように「散布図の点は重なっている」かもしれないからです。
4は、2回目の得点が1回目の得点より10点以上高く、1回目が55点以上とっている人がいるかどうかを、散布図から探してみましょう。例えば、1回目が55点以上60点未満で、2回目が70点以上の人がいます。なので、これは誤っている文です。
5は、箱ひげ図を見ましょう。1回目は中央値が65点未満なので、65点以上とった生徒は半数未満です。2回目は中央値が65点以上なので、65点以上とった生徒は半数以上です。そのため、65点以上とった生徒の数は、1回目のテストより2回目のテストの方が多いことがわかります。正しい文です。
以上から、誤っているものは、1と4であることがわかります。
解答
セソ:1・4
参考
解答編 つづき
問題
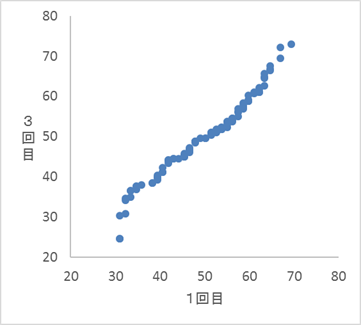
(3) 次の表3は、1回目のテストの得点と2回目のテストの得点の平均点と標準偏差の値であり、図3は、この2つのテストの得点の散布図である。ただし、表3の数値は正確な値であり、四捨五入されていないものとする。また、図3の散布図の点は重なっていることもある。
表3 平均点 標準偏差 1回目の得点 61.9 8.4 3回目の得点 133.3 26.0 
図3 ここで、2つのテストの得点をそれぞれ、次の計算式により新しい得点に換算した。\[ 新しい得点 = 50 + 10 \times \frac{得点の偏差}{標準偏差} \quad \cdots (*) \]
次の $\mybox{タ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
1回目の得点を式 (*) により換算した新しい得点と3回目の得点と式 (*) により換算した新しい得点の散布図は $\myBox{タ}$ である。
01 2
2 3
3
解説
新しい得点に換算する式を見て、得点がどう変わるか考えてみましょう。
まず、「得点の偏差」とは、得点と平均との差のことです。得点が高いほど、偏差の値も大きくなります。次に、これを標準偏差で割っています。標準偏差は正の数なので、やはり、得点が高いほど、計算結果は大きくなります。
これに、さらに10を掛けて50を足したものが新しい得点です。このことから、換算前の得点が高ければ、換算後の得点も高く、換算前が低ければ換算後も低いことがわかります。
つまり、散布図は上下や左右に圧縮されたり広がったりするかもしれませんが、大小関係が入れ替わったりすることはない、ということがわかります。
このことに注意して、散布図を見ていきましょう。
0は、1回目が高ければ3回目も高く、1回目が低ければ3回目も低くなっています。しかし、もとの散布図はそうはなっていません。そのため、0は間違いです。同様に、3も違います。問題文にあるような換算によって、順番が変わることはありません。
次に、特徴的な点を見て、それらが変換後の散布図にどう反映されているかを見てみましょう。もとの散布図では、3回目に190点近く取った人が2人います。片方は、1回目が50点程度ですね。また、1回目が70点近くで3回目が70点弱だった人もいます。
これらの人は、変換後でも散布図の同じようなところにいるはずです。1を見てみると、きちんと上の方と下の方にこれらに対応する点がありますが、2はそうなっていません。
以上から、対応する散布図は1であることがわかります。
解答
タ:1