センター試験 数学I・数学A 2017年度追試 第5問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
二等辺三角形 ABC において、 $\mathrm{ AB }=\mathrm{ AC }=2$, $\mathrm{ BC }=3$ とする。
直線 AC 上に、 C とは異なる点 D を $\angle \mathrm{ ABC }=\angle \mathrm{ ABD }$ を満たすようにとると、 $\dfrac{\mathrm{ AD } }{\mathrm{ BD } } = \dfrac{\myBox{ア} }{\myBox{イ} }$ である。 $\triangle \mathrm{ ABD }$ と $\triangle \mathrm{ BCD }$ において、 $\angle \mathrm{ ABD }=\angle \mathrm{ BCD }$ で $\angle \mathrm{ D }$ は共通であるから、 $\dfrac{\mathrm{ BD } }{\mathrm{ CD } } = \dfrac{\myBox{ウ} }{\myBox{エ} }$ である。 $\dfrac{\mathrm{ AD } }{\mathrm{ CD } } = \dfrac{\mathrm{ AD } }{\mathrm{ BD } } \cdot \dfrac{\mathrm{ BD } }{\mathrm{ CD } }$ に着目すると、$\mathrm{ CD } = \dfrac{\myBox{オカ} }{\myBox{キ} }$ である。
$\triangle \mathrm{ BCD }$ の外接円を O とし、点 B における円 O の接線と直線 AC との交点を E とすると、点 E は辺 AC の A の側の延長上にある。このとき\[ \angle \mathrm{ DBE } = \frac{\myBox{ク} }{\myBox{ケ} } \angle \mathrm{ ABE } \]であるから、 $\dfrac{\mathrm{ DE } }{\mathrm{ BE } } = \dfrac{\myBox{コ} }{\myBox{サ} }$ である。
また、線分 BE は線分 $\myBox{シ}$ と同じ長さである。 $\mybox{シ}$ に当てはまるものを、次の 0 ~ 4 のうちから一つ選べ。0: AB
1: AD
2: AE
3: BC
4: CDしたがって、$\mathrm{ DE } = \dfrac{\myBox{スセ} }{\myBox{ソ} }$ である。
辺 BC の中点を M とし、線分 EM と線分 BD の交点を F とすると\[ \dfrac{\mathrm{ FM } }{\mathrm{ EF } } = \dfrac{\myBox{タ} }{\myBox{チツ} } \]である。
考え方
同じ大きさの角度を使って、二等分線や二等辺三角形と絡ませて解いていきます。
最後は、式の形からメネラウスの定理を使うんじゃないか、と予想できますが、なかなかひらめきにくいです。求めたい比に含まれる辺を持つ三角形を探して考えましょう。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
二等辺三角形 ABC において、 $\mathrm{ AB }=\mathrm{ AC }=2$, $\mathrm{ BC }=3$ とする。
直線 AC 上に、 C とは異なる点 D を $\angle \mathrm{ ABC }=\angle \mathrm{ ABD }$ を満たすようにとると、 $\dfrac{\mathrm{ AD } }{\mathrm{ BD } } = \dfrac{\myBox{ア} }{\myBox{イ} }$ である。
解説
図は次のようになっています。
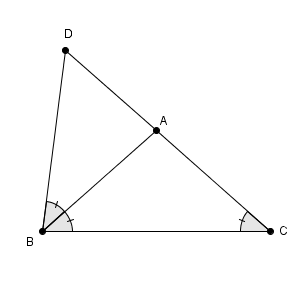
AB が $\angle \mathrm{ DBC }$ の二等分線になっている、と考えると\[ \mathrm{ BD }:\mathrm{ BC }=\mathrm{ AD }:\mathrm{ AC } \]となります。これより
\begin{eqnarray}
\frac{\mathrm{ AD } }{\mathrm{ BD } }
=
\frac{\mathrm{ AC } }{\mathrm{ BC } }
=
\frac{2}{3}
\end{eqnarray}となります。
解答
アイ:23
解答編 つづき
問題
$\triangle \mathrm{ ABD }$ と $\triangle \mathrm{ BCD }$ において、 $\angle \mathrm{ ABD }=\angle \mathrm{ BCD }$ で $\angle \mathrm{ D }$ は共通であるから、 $\dfrac{\mathrm{ BD } }{\mathrm{ CD } } = \dfrac{\myBox{ウ} }{\myBox{エ} }$ である。 $\dfrac{\mathrm{ AD } }{\mathrm{ CD } } = \dfrac{\mathrm{ AD } }{\mathrm{ BD } } \cdot \dfrac{\mathrm{ BD } }{\mathrm{ CD } }$ に着目すると、$\mathrm{ CD } = \dfrac{\myBox{オカ} }{\myBox{キ} }$ である。
解説

$\triangle \mathrm{ ABD }$ と $\triangle \mathrm{ BCD }$ において、 $\angle \mathrm{ ABD }=\angle \mathrm{ BCD }$ で $\angle \mathrm{ D }$ は共通であるから、この2つの三角形は相似になります。よって、
\begin{eqnarray}
\frac{\mathrm{ BD } }{\mathrm{ CD } }
=
\frac{\mathrm{ AD } }{\mathrm{ BD } }
=
\frac{2}{3}
\end{eqnarray}となります。最後は、アイの結果を使っています。
これより、
\begin{eqnarray}
\frac{\mathrm{ AD } }{\mathrm{ CD } }
&=&
\frac{\mathrm{ AD } }{\mathrm{ BD } } \cdot \frac{\mathrm{ BD } }{\mathrm{ CD } } \\[5pt]
&=&
\frac{2}{3} \cdot \frac{2}{3} \\[5pt]
&=&
\frac{4}{9} \\[5pt]
\end{eqnarray}が得られ、\[ \mathrm{ CD }=\mathrm{ AD }+\mathrm{ AC }=\mathrm{ AD }+2 \]であることも使うと、
\begin{eqnarray}
\mathrm{ AD } &=& \frac{4}{9} \mathrm{ CD } \\[5pt]
\mathrm{ AD } &=& \frac{4}{9} ( \mathrm{ AD } +2 ) \\[5pt]
\frac{5}{9} \mathrm{ AD } &=& \frac{8}{9} \\[5pt]
\mathrm{ AD } &=& \frac{8}{5} \\[5pt]
\end{eqnarray}となります。これから\[ \mathrm{ CD }=\mathrm{ AD }+2=\frac{18}{5} \]が得られます。
解答
ウエ:23
オカキ:185
解答編 つづき
問題
$\triangle \mathrm{ BCD }$ の外接円を O とし、点 B における円 O の接線と直線 AC との交点を E とすると、点 E は辺 AC の A の側の延長上にある。このとき\[ \angle \mathrm{ DBE } = \frac{\myBox{ク} }{\myBox{ケ} } \angle \mathrm{ ABE } \]であるから、 $\dfrac{\mathrm{ DE } }{\mathrm{ BE } } = \dfrac{\myBox{コ} }{\myBox{サ} }$ である。
解説
図は次のようになっています。
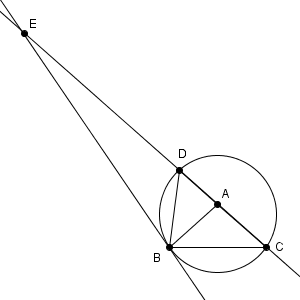
接弦定理より、 $\angle \mathrm{ DBE }=\angle \mathrm{ BCD }$ が成り立ちます。また、 $\angle \mathrm{ BCD }$ は、 $\angle \mathrm{ ABC }$ とも等しく、 $\angle \mathrm{ ABD }$ とも等しいため、\[ \angle \mathrm{ DBE } = \frac{1}{2} \angle \mathrm{ ABE } \]となります。
つまり、 $\mathrm{ DB }$ は $\angle \mathrm{ ABE }$ の二等分線なので\[ \mathrm{ EB }:\mathrm{ AB }=\mathrm{ DE }:\mathrm{ AD } \]が成り立つため、\[ \frac{\mathrm{ DE } }{\mathrm{ BE } } = \frac{\mathrm{ AD } }{\mathrm{ AB } } = \frac{8}{5} \div 2 = \frac{4}{5} \]となります。
解答
クケ:12
コサ:45
解答編 つづき
問題
また、線分 BE は線分 $\myBox{シ}$ と同じ長さである。 $\mybox{シ}$ に当てはまるものを、次の 0 ~ 4 のうちから一つ選べ。
0: AB
1: AD
2: AE
3: BC
4: CDしたがって、$\mathrm{ DE } = \dfrac{\myBox{スセ} }{\myBox{ソ} }$ である。
解説

三角形 ABC について考えると、 $\angle \mathrm{ BAE }=2\angle \mathrm{ ABC }$ です。また、クケの部分から $\angle \mathrm{ ABE }=2\angle \mathrm{ ABC }$ もわかります。よって、三角形 $\mathrm{ ABE }$ は、 $\mathrm{ AE }=\mathrm{ BE }$ の二等辺三角形であることがわかります。
よって、\[ \mathrm{ DE }=\mathrm{ AE }-\mathrm{ AD }=\mathrm{ EB }-\frac{8}{5} \]が成り立ちます。また、コサの結果も使うと
\begin{eqnarray}
\mathrm{ DE } &=& \mathrm{ EB }-\frac{8}{5} \\[5pt]
\frac{4}{5}\mathrm{ EB } &=& \mathrm{ EB }-\frac{8}{5} \\[5pt]
-\frac{1}{5}\mathrm{ EB } &=& -\frac{8}{5} \\[5pt]
\mathrm{ EB } &=& 8 \\[5pt]
\end{eqnarray}となるため、\[ \mathrm{ DE }=\mathrm{ EB }-\frac{8}{5}=8-\frac{8}{5}=\frac{32}{5} \]が得られます。
解答
シ:2
スセソ:325
解答編 つづき
問題
辺 BC の中点を M とし、線分 EM と線分 BD の交点を F とすると\[ \dfrac{\mathrm{ FM } }{\mathrm{ EF } } = \dfrac{\myBox{タ} }{\myBox{チツ} } \]である。
解説
図はこうなっています。
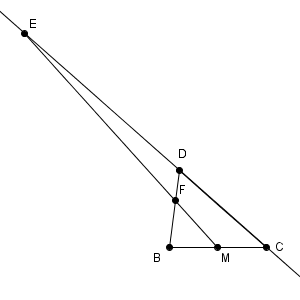
図に線を足していくとわかりづらくなりますが、使うのは上の通りです。式の形からチェバの定理やメネラウスの定理を使うことが予想されますが、これらを使うためには、 $\mathrm{ FM }$ や $\mathrm{ EF }$ が出てくる三角形を考えなければいけません。
試行錯誤すると、上のように、三角形 $\mathrm{ CEM }$ と直線 $\mathrm{ DB }$ に対して、メネラウスの定理を使えばいいことがわかります。適用すると
\begin{eqnarray}
\frac{\mathrm{ FM } }{\mathrm{ EF } } \cdot \frac{\mathrm{ BC } }{\mathrm{ MB } } \cdot \frac{\mathrm{ DE } }{\mathrm{ CD } } &=& 1 \\[5pt]
\frac{\mathrm{ FM } }{\mathrm{ EF } } \cdot 2 \cdot \left(\frac{32}{5} \div \frac{18}{5}\right) &=& 1 \\[5pt]
\frac{\mathrm{ FM } }{\mathrm{ EF } } \cdot \frac{32}{9} &=& 1 \\[5pt]
\frac{\mathrm{ FM } }{\mathrm{ EF } } &=& \frac{9}{32} \\[5pt]
\end{eqnarray}が得られます。
解答
タチツ:932





