【基本】相関係数

🕒 2016/11/17 🔄 2023/05/01

【基本】散布図では、2つのデータの関係を視覚的に把握するために、散布図や相関表が使えることを見ました。しかし、「関係があること」を、より厳密に表現できた方がいいですよね。ここでは、2つのデータの関係性を数値で表す、共分散や相関係数について見ていきます。

📘 目次

相関関係

散布図を見ると、2つのデータに「片方が大なら、もう片方も大」といった関係性が見える場合があります。このように、「一方が増えると、片方も増える」傾向がある場合、正の相関関係がある、といいます。正の相関があるともいいます。散布図が次のようになっていた場合、正の相関関係がある、といえます。

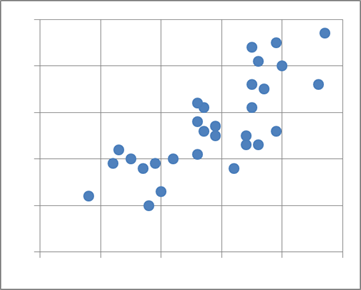
一方、「一方が増えると、片方が減る」傾向がある場合、負の相関関係がある、といいます。負の相関があるともいいます。散布図が次のようになっていた場合、負の相関関係がある、といえます。

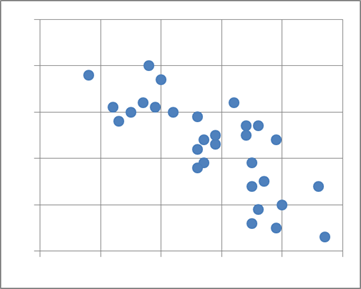
また、どちらの傾向もない場合には、2つの変量の間には相関関係がないといったり、無相関である、といったりします。散布図が次のようになっていた場合、相関関係がない、といえるでしょう。

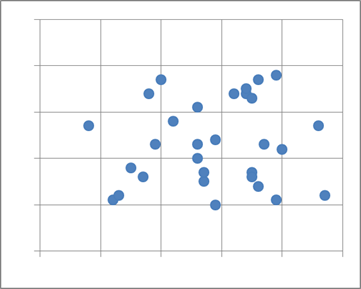
一次関数のように、ぴったり一直線上に分布することは少ないですが、ある直線に近い場合は「相関関係が強い」、そうでない場合は「相関関係が弱い」といいます。

なお、相関関係があるからといって、因果関係があるとは限りません。相関関係はあくまでも値の関係性だけを見ているだけであり、片方が原因でもう片方が起こる因果関係がある証拠にはなりません。

まったく因果関係がないにもかかわらず、たまたま相関関係が見られるケースもあります。

共分散

相関関係がある・ない、強い・弱いという話をしましたが、散布図から判断するというのは少しあいまいですよね。もう少し厳密に数値で把握したいところです。

今考えたいのは、「片方が増えると、もう片方はどうなるか？」です。なので、「片方が増えたときにもう片方が増えたら、プラスになりやすく」「片方が増えたときにもう片方が減ったら、マイナスになりやすい」値を考えればいいことがわかります。

そこでよく使われるのが、共分散という指標です。共分散(covariance)は、各偏差の積の平均値で定義されます。式で書くと次のようになります。

共分散

2組の対応するデータの値を $x_1, x_2,\cdots,x_n$ と $y_1,y_2,\cdots,y_n$ とし、それぞれの平均値を $\bar{x}$, $\bar{y}$ とする。
このとき、共分散 $s_{xy}$ は、次で表される。
\[ s_{xy} = \frac{1}{n} \{ (x_1-\bar{x})(y_1-\bar{y}) +(x_2-\bar{x})(y_2-\bar{y}) +\cdots +(x_n-\bar{x})(y_n-\bar{y}) \} \]

少しごつい式ですが、詳しく見ていきましょう。

「片方が増えると、もう片方はどうなるか？」を考えたいんでしたね。上の式では、「増える」というものを、平均値からの増加分と考えています。

項の1つ、 $(x_k-\bar{x})(y_k-\bar{y})$ について考えてみましょう。 $x_k$ と $y_k$ について、平均値からの増減が一致していれば、積はプラスになるので、上の式の値は増えます。逆に、平均値からの増減が反対だと、積は負になるので上の式の値は減ります。 $x_k$, $y_k$ の値と、 $(x_k-\bar{x})(y_k-\bar{y})$ の符号の関係は次のようになります。

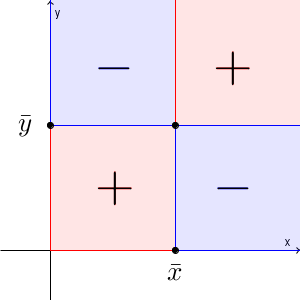
共分散の定義に出てくる式は、「片方が増えたときにもう片方が増えたら、共分散の値は増えやすく」「片方が増えたときにもう片方が減ったら、共分散の値は減りやすい」というのが実現できているわけですね。このため、共分散が正のときは「正の相関関係がある」と考えられ、負のときは「負の相関関係がある」と考えられます。

この「平均値からの差」に着目した指標は、過去にも出てきました。分散です。復習の意味を込めて、式をもう一度見てみましょう。

\[ \frac{1}{n}\left\{ (x_1-\bar{x})^2 +(x_2-\bar{x})^2 +\cdots +(x_n-\bar{x})^2 \right\} \]

見比べてみると、分散では「$x_k$ の偏差 × $x_k$ の偏差」だった部分が、共分散では「$x_k$ の偏差 × $y_k$ の偏差」になっていることがわかります。

相関係数

上の共分散のところで、次のように書きました。

共分散が正のときは「正の相関関係がある」と考えられ、負のときは「負の相関関係がある」と考えられます。

なぜ「相関関係がある」ではなく、「相関関係があると考えられる」となっているかというと、共分散では、無相関との違いがわかりにくいからなんですね。無相関のときに、共分散がぴったりゼロになるわけではありません。共分散では、相関関係の強さまでは表現できないので、「相関関係があるのか、ほとんどないのか」はわかりません。

相関関係の強さを表す指標としてよく使われるのが、相関係数(correlation coefficient)です。相関係数は、共分散をそれぞれの標準偏差で割ったものです。

相関係数

2組の対応するデータの標準偏差を $s_x$, $s_y$ とし、共分散を $s_{xy}$ とするとき、相関係数 $r_{xy}$ は次の式で表される。\[ r_{xy} = \frac{s_{xy} }{s_x s_y} \]

ここでは示しませんが、相関係数は、-1以上1以下となることが知られています（証明は今の段階では難しいです）。また、次のような性質があります。

相関係数の性質