【発展】回帰直線
ここでは、散布図のすべての点にできるだけ合うように引いた直線である回帰直線について見ていきます。少し計算が複雑ですが、求め方についても見ていきます。
回帰直線
2つの変量の関係を視覚的にとらえたいときには、散布図を使うといいのでした。
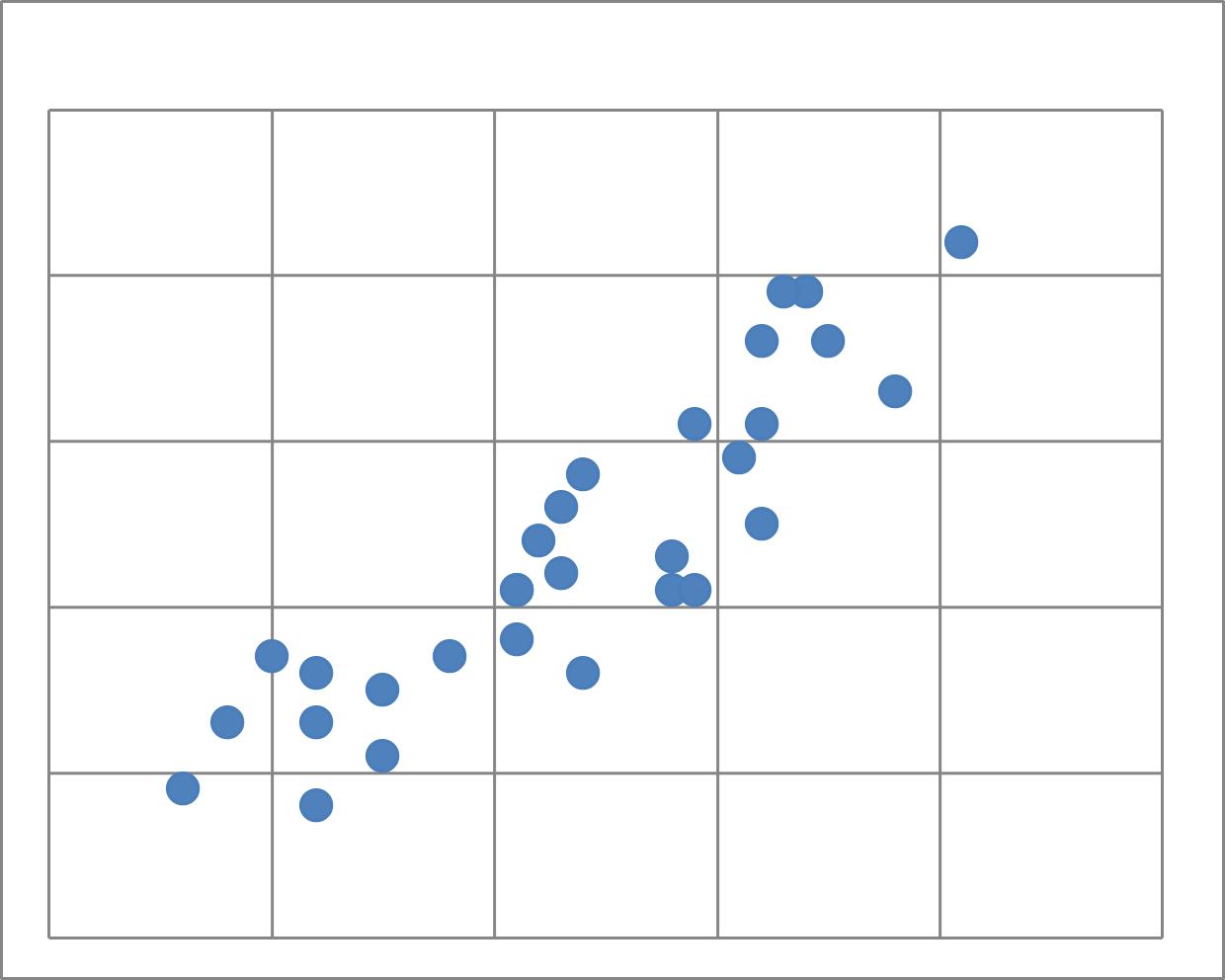
すべての点が直線上に並ぶことはほとんどないですが、ある直線に近いところに散らばっていることはあります。ある直線の近くに散らばっているほど相関が強い、というのでしたね。
このとき、その直線を実際にひいてみましょう。手で適当にひくと、次のようになるでしょう。
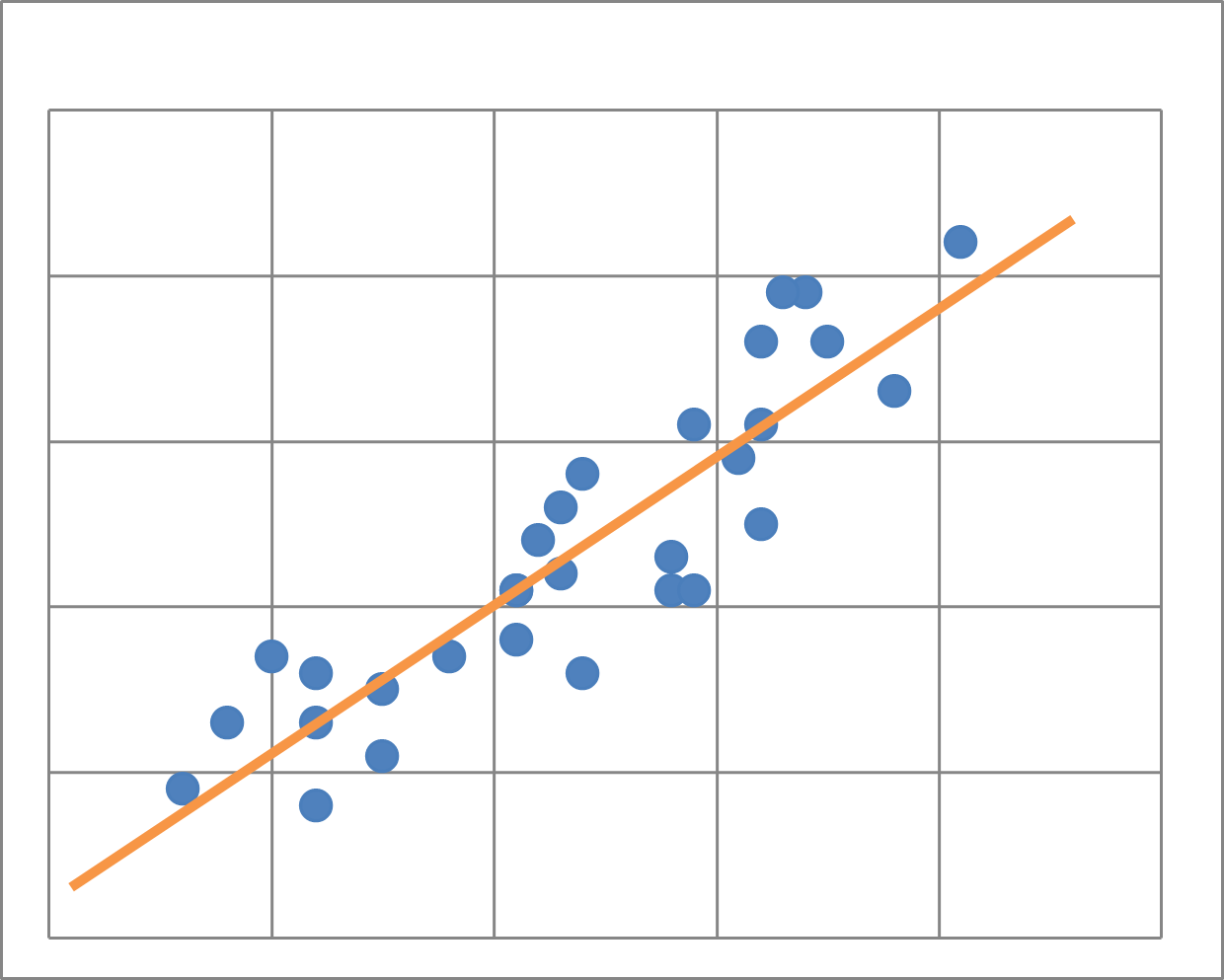
この直線はどう決めるのがいいでしょうか。以下では、この直線の決め方を見ていきます。
散布図上の点を $(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)$ とします。一般には、散布図とは2つの変量の関係を見るものであり対等な関係ですが、ここでは、 $x_k$ を使って $y_k$ を表したい、とします。また、直線の方程式を $y=ax+b$ とおきます。
もし、すべての点がある直線上にあったら、すべての $k$ について、 $y_k=ax_k+b$ が成り立ちます。つまり、直線 $y=ax+b$ 上にあるはずです。
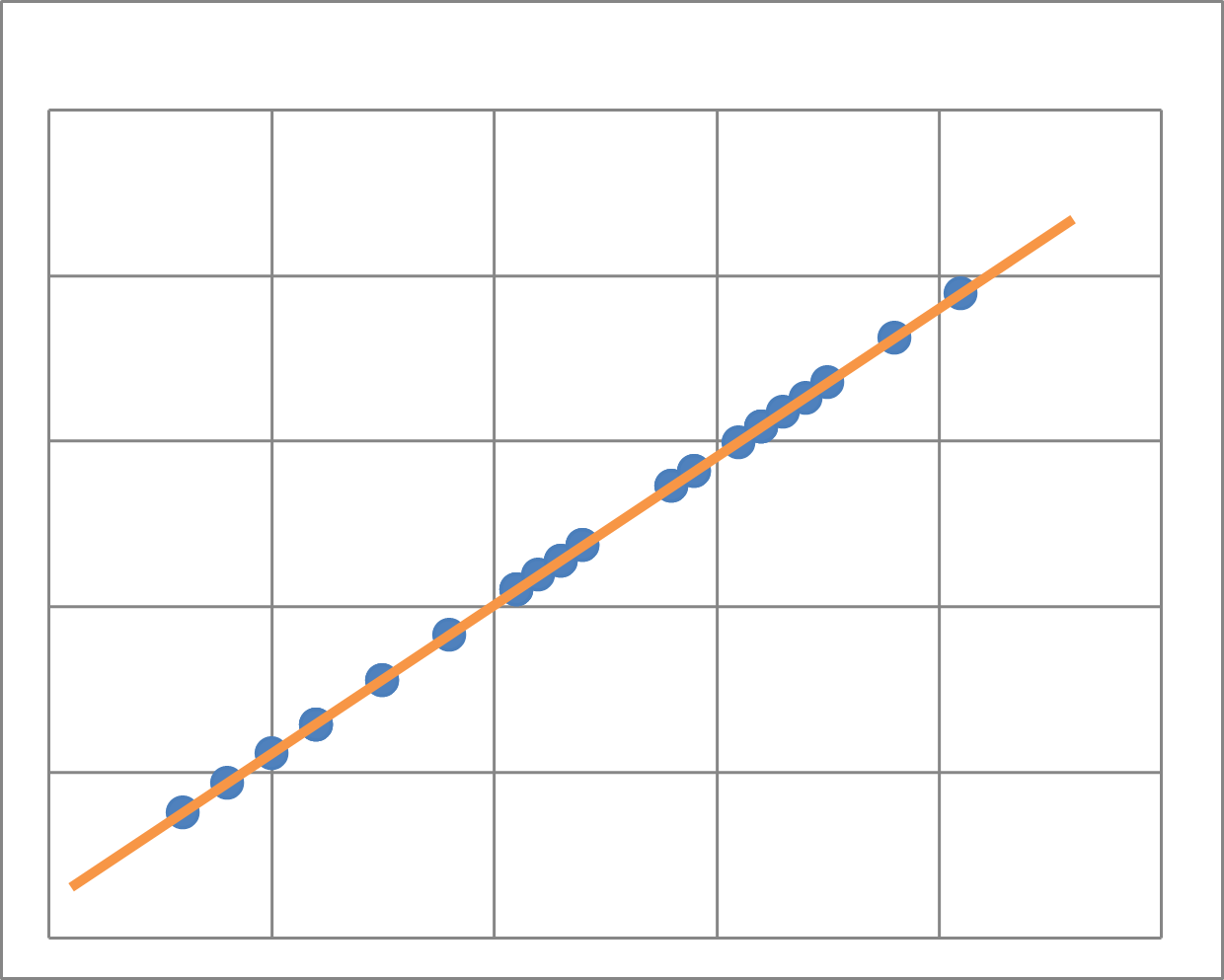
しかし、実際にはそんなにきれいにはいかなくて、ズレが生じます。

このズレをそれぞれ2乗し、その和が最小になるような直線を求めます。この直線のことを、回帰直線(regression line) といいます。
ズレを2乗して足したものとは、散布図と直線のズレをまとめたものになります。これが最小になるものを考えるのは、 $x$ から $y$ を表現するときにトータルの誤差をできるだけ少なくしたい、というところからきています。
回帰直線の求め方
では、具体的に計算して、直線の方程式を求めてみましょう。文字は先ほどと同じ設定をそのまま使うことにします。
$x_k$ に対して、直線上では $ax_k+b$ が対応しますが、実際に対応する値は $y_k$ です。なので、ズレの2乗は\[ (y_k-ax_k-b)^2 \]となります。これを、まず、 $b$ の関数だと思って次のように展開しましょう。
\begin{eqnarray}
& & (y_k-ax_k-b)^2 \\[5pt]
&=& b^2 -2(y_k-ax_k)b +(y_k-ax_k)^2 \\[5pt]
&=& b^2 -2y_kb+2ax_kb +(y_k-ax_k)^2 \\[5pt]
\end{eqnarray}
$b$ について見ると二次関数なので、平方完成すれば最小になるときが求められそうですね。この式をすべての $k$ について足すと次のようになります。
\begin{eqnarray}
& & nb^2 -2(y_1+y_2+\cdots+y_n)b \\
& & +2a(x_1+x_2+\cdots+x_n)b \\
& & +(y_1-ax_1)^2\cdots+(y_n-ax_n)^2
\end{eqnarray}
計算結果を詳しく見てみましょう。 $b^2$ は $n$ 個足されるので、係数は $n$ となります。 $b$ の項は $-2y_kb+2ax_kb$ を足していくので、 $y_1+y_2+\cdots+y_n$ や $x_1+x_2+\cdots+x_n$ が出てきます。ところで、これらは、平均値の $n$ 倍です。平均値を $\bar{x}$ や $\bar{y}$ で表すことにしましょう。また、残りの項は $b$ の入っていない定数項なので、とりあえず $C$ とおくことにすると、上の式は次のように変形できます。
\begin{eqnarray}
& & nb^2 -2\cdot n\bar{y}\cdot b +2a\cdot n\bar{x}\cdot b +C \\[5pt]
&=& nb^2 -2n(\bar{y}-a\bar{x})b +C \\[5pt]
&=& n\left\{ b- (\bar{y}-a\bar{x}) \right\}^2 -n(\bar{y}-a\bar{x})^2 +C \\[5pt]
\end{eqnarray}
つまり、 $b=\bar{y}-a\bar{x}$ のときに誤差の2乗の合計が最小になることがわかります。
まだ切片の $b$ がわかっただけなので、次は傾き $a$ を考えます。残っていた部分である\[ -n(\bar{y}-a\bar{x})^2 +C \]が最小となる場合を考えればいいですね。ここには $b$ は含まれていないので、 $a$ の式だと思って変形していきます。
先ほど、 $C$ は $(y_k-ax_k)^2$ を $k=1$ から $n$ まで足したものと置きました。 $k$ 番目の式を展開すると\[ y_k^2 -2ax_ky_k +a^2x_k^2 \]となります。これを踏まえ、次のように $D_x,D_{xy}, D_y$ という3つの文字を置くことにしましょう。
\begin{eqnarray}
D_{x} &=& x_1^2 +x_2^2+\cdots+x_n^2 \\[5pt]
D_{xy} &=& x_1y_1 +x_2y_2+\cdots+x_ny_n \\[5pt]
D_{y} &=& y_1^2 +y_2^2+\cdots+y_n^2 \\[5pt]
\end{eqnarray}
こうすると、 $-n(\bar{y}-a\bar{x})^2 +C$ は次のように書けます。
\begin{eqnarray}
& &
-n(\bar{y})^2 +2an\bar{x}\bar{y} -a^2n(\bar{x})^2 +D_y -2aD_{xy} +a^2D_x \\[5pt]
&=&
( D_x-n(\bar{x})^2 )a^2 -2(D_{xy}-n\bar{x}\bar{y})a +D_y-n(\bar{y})^2 \\[5pt]
\end{eqnarray}$a$ の二次関数なので、平方完成をすると
\[ ( D_x-n(\bar{x})^2 ) \left(a -\frac{D_{xy}-n\bar{x}\bar{y}}{D_x-n(\bar{x})^2} \right)^2 +\cdots \]となります。なお、 $a$ を含まない部分は省略しています。
この変形から、\[ \frac{D_{xy}-n\bar{x}\bar{y}}{D_x-n(\bar{x})^2} \]という値がキーになっていると考えられます。
なかなかヘビーな式ですが、もう少し簡潔に表すことができます。別ページで求めた結果を使います。【標準】データの分散で求めた通り、分散は「2乗の平均 引く 平均の2乗」で表すことができます。また、【発展】共分散のもう一つの求め方で見た通り、共分散は「積の平均 引く 平均の積」でも求めることができます。
これらを踏まえ、 分散を $s_x^2$, 共分散を $s_{xy}$ とおくと、
\begin{eqnarray}
\dfrac{1}{n} D_x -(\bar{x})^2 &=& s_x^2 \\[5pt]
\frac{1}{n}D_{xy}-\bar{x}\bar{y} &=& s_xs_y \\[5pt]
\end{eqnarray}が成り立ちます。なので、先ほど「これがキー」といっていた値は、
\begin{eqnarray}
& & \frac{D_{xy}-n\bar{x}\bar{y}}{D_x-n(\bar{x})^2} \\[5pt]
&=& \frac{\frac{1}{n}D_{xy}-\bar{x}\bar{y}}{\frac{1}{n}D_x-(\bar{x})^2} \\[5pt]
&=& \frac{s_{xy}}{s_x^2} \\[5pt]
\end{eqnarray}と変形できます。また、 $-n(\bar{y}-a\bar{x})^2 +C$ は\[ s_x^2 \left( a-\frac{s_{xy}}{s_x^2} \right)^2+\cdots \]と変形でき(省略しているところは $a$ を含まない式)、 $s_x\ne 0$ の場合は、 $a=\dfrac{s_{xy}}{s_x^2}$ のときに最小値をとることがわかります。なので、これが回帰直線の傾きとなります。
まとめると、 $x$ の分散を $s_x^2$, 共分散を $s_{xy}$ とし、平均を $\bar{x}$, $\bar{y}$ とおくと、回帰直線 $y=ax+b$ は\[ a=\frac{s_{xy}}{s_x^2},\quad b=\bar{y}-a\bar{x} \]となります。
言葉で書けば、
- 傾き:($x$ と $y$ の共分散)÷($x$ の分散)
- 切片:($y$ の平均)-(傾き)×($x$ の平均)
おわりに
ここでは、回帰直線とその求め方について見てきました。最後の結果はわりとシンプルですが、途中の計算はわりとヘビーですね。やっていることは二次関数の最小値を求める計算だけですが、文字が多いので計算は大変です。





