センター試験 数学I・数学A 2016年度 第5問 解説
問題編
問題
四角形ABCDにおいて、$\mathrm{AB}=4、\mathrm{BC}=2、\mathrm{DA}=\mathrm{DC}$ であり、4つの頂点A、B、C、Dは同一円周上にある。対角線ACと対角線BDの交点をE、線分ADを $2:3$ の比に内分する点をF、直線FEと直線DCの交点をGとする。
参考図次の $\mybox{ア}$ には、下の 0~4 のうちから当てはまるものを一つ選べ。
$\angle\mathrm{ABC}$ の大きさが変化するとき四角形ABCD の外接円の大きさも変化することに注意すると、$\angle\mathrm{ABC}$ の大きさがいくらであっても、$\angle\mathrm{DAC}$ と大きさが等しい角は、$\angle\mathrm{DCA}$ と $\angle\mathrm{DBC}$ と $\myBox{ア}$ である。
0: $\angle\mathrm{ABD}$
1: $\angle\mathrm{ACB}$
2: $\angle\mathrm{ADB}$
3: $\angle\mathrm{BCG}$
4: $\angle\mathrm{BEG}$このことより $\displaystyle \frac{\mathrm{EC} }{\mathrm{AE} }=\frac{\myBox{イ}}{\myBox{ウ}}$ である。次に、$\triangle\mathrm{ACD}$ と直線FE に着目すると、$\displaystyle \frac{\mathrm{GC} }{\mathrm{DG} }=\frac{\myBox{エ}}{\myBox{オ}}$ である。
(1) 直線AB が点G を通る場合について考える。
このとき、$\triangle \mathrm{AGD}$ の辺AG 上に点B があるので、$\mathrm{BG}=\myBox{カ}$ である。
また、直線AB と直線DC が点G で交わり、4点A、B、C、D は同一円周上にあるので、$\mathrm{DC}=\myBox{キ}\sqrt{\myBox{ク}}$である。
(2) 四角形ABCD の外接円の直径が最小となる場合について考える。
このとき、四角形ABCD の外接円の直径は $\myBox{ケ}$ であり、$\angle \mathrm{BAC}=\myBox{コサ}^{\circ}$ である。
また、直線FE と直線AB の交点を H とするとき、$\displaystyle \frac{\mathrm{GC} }{\mathrm{DG} }=\frac{\mybox{エ}}{\mybox{オ}}$ の関係に着目して AH を求めると、$\mathrm{AH}=\myBox{シ}$ である。
考え方
参考図が描かれていますが、これは本当にただの参考図で、(1)も(2)も図を描きなおさないといけません。特に(2)は図を描くのが少し大変です。ごちゃっとしてしまいがちです。どの状況でどの定理を用いるかをきちんと判断していかないと進めないので、少し難易度が高い問題です。チェバの定理やメネラウスの定理といった基本的な定理を使いこなす必要があります。
解答編
問題
四角形ABCDにおいて、$\mathrm{AB}=4、\mathrm{BC}=2、\mathrm{DA}=\mathrm{DC}$ であり、4つの頂点A、B、C、Dは同一円周上にある。対角線ACと対角線BDの交点をE、線分ADを $2:3$ の比に内分する点をF、直線FEと直線DCの交点をGとする。
参考図次の $\mybox{ア}$ には、下の 0~4 のうちから当てはまるものを一つ選べ。
$\angle\mathrm{ABC}$ の大きさが変化するとき四角形ABCD の外接円の大きさも変化することに注意すると、$\angle\mathrm{ABC}$ の大きさがいくらであっても、$\angle\mathrm{DAC}$ と大きさが等しい角は、$\angle\mathrm{DCA}$ と $\angle\mathrm{DBC}$ と $\myBox{ア}$ である。
0: $\angle\mathrm{ABD}$
1: $\angle\mathrm{ACB}$
2: $\angle\mathrm{ADB}$
3: $\angle\mathrm{BCG}$
4: $\angle\mathrm{BEG}$
解説
Dについては、DA=DCという条件しかなく、長さは確定しません。なので、この四角形の形は確定しないんですね。しかし、どんな形であっても、$\angle\mathrm{DAC}$と同じ角になるものがあるから、まずはそれを探しなさい、というのが最初の問題です。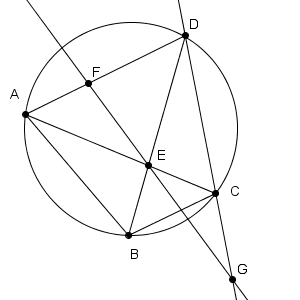
DA=DCから、$\angle\mathrm{DAC}$と$\angle\mathrm{DCA}$は同じ角度です。弧CDに着目すると、$\angle\mathrm{DAC}$と$\angle\mathrm{DBC}$も同じです。また、弧ADに注目すると、$\angle\mathrm{DCA}$と$\angle\mathrm{ABD}$は同じ角度です。よって、アには、$\angle\mathrm{ABD}$が入ります。
解答
ア:0解答編 つづき
問題
このことより $\displaystyle \frac{\mathrm{EC} }{\mathrm{AE} }=\frac{\myBox{イ}}{\myBox{ウ}}$ である。

先ほどの結果から、$\angle\mathrm{ABD}$と$\angle\mathrm{DBC}$が同じ大きさであることがわかりました。これは、BEが$\angle\mathrm{ABC}$の二等分線になっている、ということでもあります。よって、
AE:EC=AB:BC=4:2なので、$\displaystyle \frac{\mathrm{EC} }{\mathrm{AE} }=\frac{1}{2}$がわかります。
解答
イウ:12解答編 つづき
問題
次に、$\triangle\mathrm{ACD}$ と直線FE に着目すると、$\displaystyle \frac{\mathrm{GC} }{\mathrm{DG} }=\frac{\myBox{エ}}{\myBox{オ}}$ である。
解説

三角形ACDと直線FEに着目すると、メネラウスの定理より
\begin{eqnarray}
\frac{\mathrm{GC} }{\mathrm{DG} } \times \frac{\mathrm{EA} }{\mathrm{CE} } \times \frac{\mathrm{FD} }{\mathrm{AF} } = 1 \\[5pt]
\frac{\mathrm{GC} }{\mathrm{DG} } \times 2 \times \frac{3}{2} = 1 \\[5pt]
\frac{\mathrm{GC} }{\mathrm{DG} } = \frac{1}{3}
\end{eqnarray}
が得られます。
解答
エオ:13解答編 つづき
問題
(1) 直線AB が点G を通る場合について考える。
このとき、$\triangle \mathrm{AGD}$ の辺AG 上に点B があるので、$\mathrm{BG}=\myBox{カ}$ である。
また、直線AB と直線DC が点G で交わり、4点A、B、C、D は同一円周上にあるので、$\mathrm{DC}=\myBox{キ}\sqrt{\myBox{ク}}$である。
解説
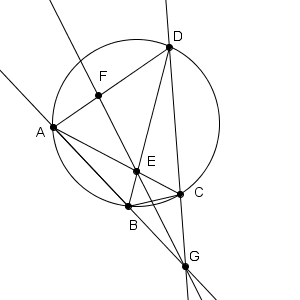
三角形ADGに着目すると、チェバの定理より
\[
\frac{\mathrm{FD} }{\mathrm{AF} } \times \frac{\mathrm{CG} }{\mathrm{DC} } \times \frac{\mathrm{BA} }{\mathrm{GB} } = 1
\]
が成り立ちます。ここで、「エオ」の部分で求めた$\displaystyle \frac{\mathrm{GC} }{\mathrm{DG} } = \frac{1}{3}$から、DG=3GCであり、CD=2GCであることがわかるので、これを用いると、
\begin{eqnarray}
\frac{\mathrm{FD} }{\mathrm{AF} } \times \frac{\mathrm{CG} }{\mathrm{DC} } \times \frac{\mathrm{BA} }{\mathrm{GB} } = 1 \\[5pt]
\frac{3}{2} \times \frac{1}{2} \times \frac{4}{\mathrm{GB} } = 1 \\[5pt]
\mathrm{BG} = 3
\end{eqnarray}
が得られます。
また、方べきの定理より、GB:GC=DG:AGが成り立ちます。ここで、BG=3だから、AG=3+4=7、DG=3CGより、この比は、3:GC=3CG:7となります。
これから、$3\mathrm{CG}^2=21$なので、$\mathrm{CG}=\sqrt{7}$となります。
よって、$\mathrm{CD}=2\mathrm{CG}=2\sqrt{7}$が得られます。
解答
カ:3キク:27
解答編 つづき
問題
(2) 四角形ABCD の外接円の直径が最小となる場合について考える。
このとき、四角形ABCD の外接円の直径は $\myBox{ケ}$ であり、$\angle \mathrm{BAC}=\myBox{コサ}^{\circ}$ である。
解説
AB=4なので、外接円の直径が4より小さくなることはありえません。また、ABが直径のときに問題の条件をみたすものが存在するので、このときが最小となります。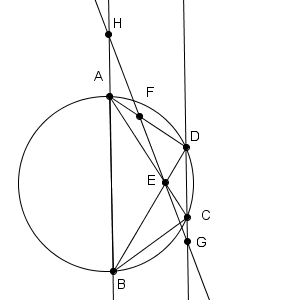
以上から、外接円が最小のときの直径は4となります。
また、このとき、三角形ABCは正三角形の半分の形であり、$\angle\mathrm{BAC}$が30度になることもわかります。
解答
ケ:4コサ:30
解答編 つづき
問題
また、直線FE と直線AB の交点を H とするとき、$\displaystyle \frac{\mathrm{GC} }{\mathrm{DG} }=\frac{\mybox{エ}}{\mybox{オ}}$ の関係に着目して AH を求めると、$\mathrm{AH}=\myBox{シ}$ である。
解説

$\angle\mathrm{BAC}$も$\angle\mathrm{DCA}$も30度なので、ABとCDは平行です。よって、AH:AB=CG:CD=1:2であり、AB=4なので、AH=2となります。





