センター試験 数学I・数学A 2016年度 第1問 [3] 解説
問題編
問題
a を1以上の定数とし、x についての連立不等式
\begin{eqnarray} \left\{ \begin{array}{ll} x^2 + (20 - a^2)x -20a^2 \leqq 0 & & \cdots ① \\ x^2 + 4ax \geqq 0 & & \cdots ② \end{array} \right. \end{eqnarray} を考える。このとき、不等式①の解は $\myBox{チツテ}\leqq x \leqq a^2$ である。また、不等式②の解は $x\leqq \myBox{トナ}a$、$\myBox{ニ}\leqq x$ である。この連立不等式を満たす負の実数が存在するような a の範囲は\[1\leqq a \leqq \myBox{ヌ}\]である。
考え方
前半は因数分解ができるので、そんなに難しくないですね。後半は図を書いて、解の範囲の共通部分が存在する条件を考えましょう。
解答編
問題
a を1以上の定数とし、x についての連立不等式
\begin{eqnarray} \left\{ \begin{array}{ll} x^2 + (20 - a^2)x -20a^2 \leqq 0 & & \cdots ① \\ x^2 + 4ax \geqq 0 & & \cdots ② \end{array} \right. \end{eqnarray} を考える。このとき、不等式①の解は $\myBox{チツテ}\leqq x \leqq a^2$ である。また、不等式②の解は $x\leqq \myBox{トナ}a$、$\myBox{ニ}\leqq x$ である。
解説
\begin{eqnarray} x^2+(20-a^2)x-20a^2 \leqq 0 \\ (x+20)(x-a^2) \leqq 0 \end{eqnarray} なので、この解は、$-20\leqq x \leqq a^2$となります。また、
\begin{eqnarray}
x^2+4ax \geqq 0 \\
x(x+4a) \geqq 0
\end{eqnarray}
となり、$a$が1以上なので、この解は、$x\leqq -4a$、$0\leqq x$となります。
解答
チツテ:-20トナ:-4
ニ:0
参考
解答編 つづき
問題
この連立不等式を満たす負の実数が存在するような a の範囲は\[1\leqq a \leqq \myBox{ヌ}\]である。
解説
上で求めた結果を、図にしてみましょう。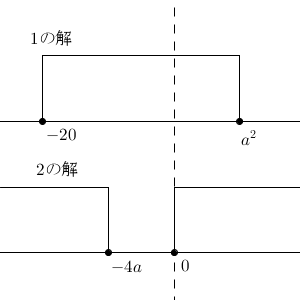
この2つの連立不等式を満たす負の実数の範囲は、$-20\leqq x \lt 0$ と $x\leqq -4a$ の共通範囲と一致します。なので、求める条件は $-20 \leqq -4a$ となります。これを解くと、 $a \leqq 5$ となります。また条件から、aは1以上なので、$1\leqq a \leqq 5$となります。
解答
ヌ:5





