センター試験 数学I・数学A 2016年度 第2問 [1] 解説
問題編
問題
$\triangle$ABC の辺の長さと角の大きさを測ったところ、 AB=$7\sqrt{3}$ および $\angle \mathrm{ACB}=60^{\circ}$ であった。したがって、 $\triangle$ABC の外接円 O の半径は $\myBox{ア}$ である。
外接円 O の、点 C を含む弧 AB 上で点 P を動かす。
(1) 2PA=3PB となるのは $\mathrm{PA}=\myBox{イ}\sqrt{\myBox{ウエ}}$ のときである。
(2) $\triangle$PAB の面積が最大となるのは $\mathrm{PA}=\myBox{オ}\sqrt{\myBox{カ}}$ のときである。
(3) $\sin \angle \mathrm{PBA}$ の値が最大となるのは $\mathrm{PA}=\myBox{キク}$ のときであり、このとき $\triangle \mathrm{PAB}$ の面積は $\displaystyle \frac{\myBox{ケコ}\sqrt{\myBox{サ}} }{\myBox{シ}}$ である。
考え方
(1)(2)(3)でそれぞれ状況が違うので、図を描き分けないといけません。
一見大変そうですが、角度の一つが60度であることを使えば、いろいろと計算を省略できます。
解答編
問題
$\triangle$ABC の辺の長さと角の大きさを測ったところ、 AB=$7\sqrt{3}$ および $\angle \mathrm{ACB}=60^{\circ}$ であった。したがって、 $\triangle$ABC の外接円 O の半径は $\myBox{ア}$ である。
解説
辺の長さと対角がわかっているので、外接円の半径は正弦定理から求められますね。
\begin{eqnarray}
\frac{\mathrm{AB} }{2\sin \angle \mathrm{ACB} } = \frac{7\sqrt{3} }{2\cdot \sqrt{3}/2}=7
\end{eqnarray}となります。
解答
ア:7
参考
解答編 つづき
問題
外接円 O の、点 C を含む弧 AB 上で点 P を動かす。
(1) 2PA=3PB となるのは $\mathrm{PA}=\myBox{イ}\sqrt{\myBox{ウエ}}$ のときである。
解説
現状は、次のような図になっています。

$\angle \mathrm{APB}$ も $60^{\circ}$ であることから、余弦定理より
\begin{eqnarray}
\mathrm{AB}^2
&=&
\mathrm{PA}^2+\mathrm{PB}^2-2\mathrm{PA}\cdot \mathrm{PB} \cos \angle 60^{\circ}
\\
147
&=&
\mathrm{PA}^2+\mathrm{PB}^2-\mathrm{PA}\cdot \mathrm{PB}
\end{eqnarray}となります。
2PA=3PB となるとき、上の式に PB=2PA/3 を代入して
\begin{eqnarray}
147&=&\mathrm{PA}^2+\mathrm{PA}^2 \cdot 4/9 - \mathrm{PA}^2 \cdot 2/3 \\
147&=&\frac{7}{9}\cdot \mathrm{PA}^2 \\
\mathrm{PA}^2&=&189 \\
\mathrm{PA}&=&3\sqrt{21}
\end{eqnarray}となります。
解答
イウエ:321参考
解答編 つづき
問題
(2) $\triangle$PAB の面積が最大となるのは $\mathrm{PA}=\myBox{オ}\sqrt{\myBox{カ}}$ のときである。
解説
もう一度図を見てみましょう。

P が動いても AB の長さは変わりません。ということは、三角形 PAB の面積が最大になるのは、AB を底辺としたときの高さが最大となるときです。
それは、P が AB の垂直二等分線上にあるとき、つまり、 PA=PB のときです。ここで、 $\angle\mathrm{ APB }$ は $60^{\circ}$ なので、このときの三角形 PAB は正三角形。よって、\[ \mathrm{ PA }=\mathrm{ AB }=7\sqrt{3} \]となります。
解答
オカ:73
解答編 つづき
問題
(3) $\sin \angle \mathrm{PBA}$ の値が最大となるのは $\mathrm{PA}=\myBox{キク}$ のときであり、このとき $\triangle \mathrm{PAB}$ の面積は $\displaystyle \frac{\myBox{ケコ}\sqrt{\myBox{サ}} }{\myBox{シ}}$ である。
解説
$\sin \angle \mathrm{PBA} $ が最大になるのは、$\angle \mathrm{PBA} $ が直角のときです。 $\angle \mathrm{APB}$ は $60^{\circ}$ なので、正三角形の半分の形ですね。
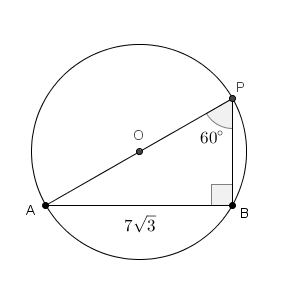
よって、\[ \mathrm{PA}=\mathrm{AB}\cdot \frac{2}{\sqrt{3} }=14 \]となります。もしくは、 PA が外接円の直径になることに注目して、[ア]の答えから、 $\mathrm{ PA }=14$ と求めることもできます。
三角形 PAB の面積は、\[ 7\sqrt{3} \cdot 7 \cdot \frac{1}{2}=\frac{49\sqrt{3} }{2} \]となります。
角度の一つが60度であることに注目すると、計算量をぐっと抑えられる問題でした。
解答
キク:14ケコサシ:4932





