センター試験 数学I・数学A 2015年度 第3問 [1] 解説

問題編

問題

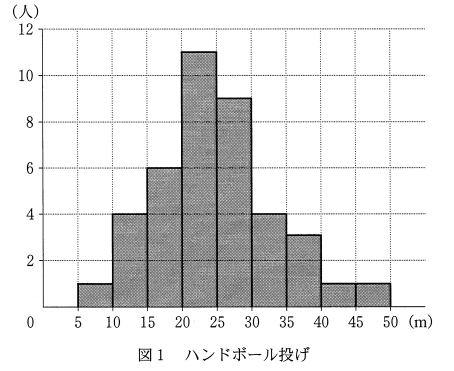
　ある高校3年生1クラスの生徒40人について、ハンドボール投げの飛距離のデータを取った。次の図1は、このクラスで最初に取ったデータのヒストグラムである。

(1) 次の $\mybox{ア}$ に当てはまるものを、下の 0 ～ 8 のうちから一つ選べ。

　この40人のデータの第３四分位数が含まれる階級は、$\myBox{ア}$ である。

　0: 5m以上 10m未満
　1: 10m以上 15m未満
　2: 15m以上 20m未満
　3: 20m以上 25m未満
　4: 25m以上 30m未満
　5: 30m以上 35m未満
　6: 35m以上 40m未満
　7: 40m以上 45m未満
　8: 45m以上 50m未満

(2) 次の $\mybox{イ}$ ～ $\mybox{オ}$ に当てはまるものを、下の 0 ～ 5 のうちから一つずつ選べ。ただし、$\mybox{イ}$ ～ $\mybox{オ}$ の解答の順序は問わない。

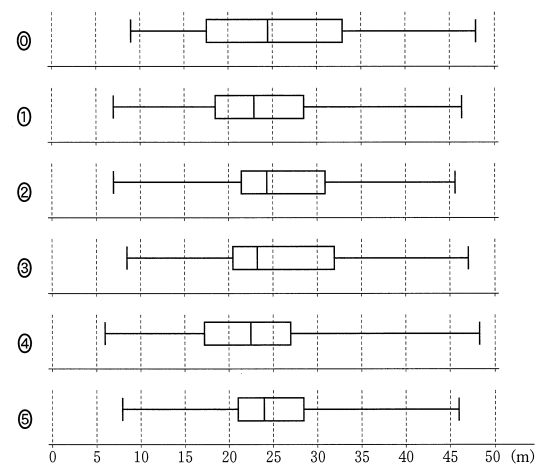
　このデータを箱ひげ図にまとめたとき、図1 のヒストグラムと矛盾するものは、 $\myBox{イ}$、$\myBox{ウ}$、$\myBox{エ}$、$\myBox{オ}$である。

(3) 次の文章中の $\mybox{カ}$、$\mybox{キ}$ に入れるものとして最も適当なものを、下の 0 ～ 3 のうちから一つずつ選べ。ただし、$\mybox{カ}$、$\mybox{キ}$ の解答の順序は問わない。

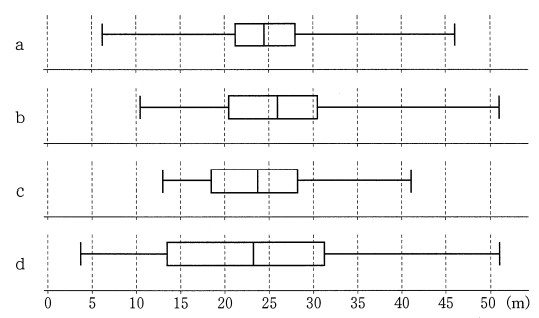
　後日、このクラスでハンドボール投げの記録を取り直した。次に示した A ～ D は、最初に取った記録から今回の記録への変化の分析結果を記述したものである。a ～ d の各々が今回取り直したデータの箱ひげ図となる場合に、0 ～ 3 の組合せのうち分析結果と箱ひげ図が矛盾するものは、$\myBox{カ}$、$\myBox{キ}$ である。

　0:A-a、　1:B-b、　2:C-c、　3:D-d

　A: どの生徒の記録も下がった。
　B: どの生徒の記録も伸びた。
　C: 最初に取ったデータで上位 $\frac{1}{3}$ に入るすべての生徒の記録が伸びた。
　D: 最初に取ったデータで上位 $\frac{1}{3}$ に入るすべての生徒の記録は伸び、下位 $\frac{1}{3}$ に入るすべての生徒の記録は下がった。

考え方

(1)は「第３四分位数」の言葉の意味が分かっていれば、グラフから読み取るだけです。

(2)は、階級が他と違うところに注目して考えます。第１四分位点と第３四分位点の階級が選択肢によって違うので、ここに注目します。

(3)は、少し面倒ですが、1つ1つ選択肢を検証していくしかありません。「記録が伸びた」といっているのに記録が下がっている箇所がないか、逆に「記録が下がった」と言っているのに記録が伸びているところがないか、チェックしていきましょう。

解答編

問題

　ある高校3年生1クラスの生徒40人について、ハンドボール投げの飛距離のデータを取った。次の図1は、このクラスで最初に取ったデータのヒストグラムである。

(1) 次の $\mybox{ア}$ に当てはまるものを、下の 0 ～ 8 のうちから一つ選べ。

　この40人のデータの第３四分位数が含まれる階級は、$\myBox{ア}$ である。

　0: 5m以上 10m未満
　1: 10m以上 15m未満
　2: 15m以上 20m未満
　3: 20m以上 25m未満
　4: 25m以上 30m未満
　5: 30m以上 35m未満
　6: 35m以上 40m未満
　7: 40m以上 45m未満
　8: 45m以上 50m未満

解説

解答

解答編 つづき

問題

(2) 次の $\mybox{イ}$ ～ $\mybox{オ}$ に当てはまるものを、下の 0 ～ 5 のうちから一つずつ選べ。ただし、$\mybox{イ}$ ～ $\mybox{オ}$ の解答の順序は問わない。

　このデータを箱ひげ図にまとめたとき、図1 のヒストグラムと矛盾するものは、 $\myBox{イ}$、$\myBox{ウ}$、$\myBox{エ}$、$\myBox{オ}$である。

解説

最大値、最小値、中央値はすべて同じ区間に入っており、これらは何も矛盾していません。問題は、第１四分位数と第３四分位数ですね。この2つがどうなっている必要があるのかを考えていきます。

(1)の通り、第３四分位数は25～30の間に入っていないといけないので、0と2と3は矛盾します。

第１四分位数については、下から10番目と11番目の平均をとれば求められますが、両方とも15～20の間に入っているので、第１四分位数もこの範囲にあることがわかります。よって、2と3と5が矛盾します。

2つを合わせると、0・2・3・5が矛盾します。

解答

解答編 つづき

問題

(3) 次の文章中の $\mybox{カ}$、$\mybox{キ}$ に入れるものとして最も適当なものを、下の 0 ～ 3 のうちから一つずつ選べ。ただし、$\mybox{カ}$、$\mybox{キ}$ の解答の順序は問わない。

　後日、このクラスでハンドボール投げの記録を取り直した。次に示した A ～ D は、最初に取った記録から今回の記録への変化の分析結果を記述したものである。a ～ d の各々が今回取り直したデータの箱ひげ図となる場合に、0 ～ 3 の組合せのうち分析結果と箱ひげ図が矛盾するものは、$\myBox{カ}$、$\myBox{キ}$ である。

　0:A-a、　1:B-b、　2:C-c、　3:D-d

　A: どの生徒の記録も下がった。
　B: どの生徒の記録も伸びた。
　C: 最初に取ったデータで上位 $\frac{1}{3}$ に入るすべての生徒の記録が伸びた。
　D: 最初に取ったデータで上位 $\frac{1}{3}$ に入るすべての生徒の記録は伸び、下位 $\frac{1}{3}$ に入るすべての生徒の記録は下がった。

解説

まず、「A:どの生徒の記録も下がった」場合。このときは、すべての値が下がっていないといけませんが、第1四分位数が20～25の間に入っており、元の15～20より記録がよくなっています。これは矛盾しています。

次に、「B:どの生徒の記録も伸びた」場合。このときは、すべての値が上がっていないといけません。箱ひげ図からは、すべての値が上がっているため、矛盾するところはありません。

「C:最初にとったデータで上位1/3に入るすべての生徒の記録が伸びた」場合。この場合、上位1/3に関連するデータ、つまり、最大値や第3四分位数は上がっていないといけません。しかし、最大値が下がっています。これは矛盾しています。

最後に「D:最初にとったデータで上位1/3に入るすべての生徒の記録は伸び、下位1/3に入るすべての生徒の記録は下がった」場合。この場合は、最大値や第3四分位数があがり、最小値や第1四分位数が下がる必要がありますが、箱ひげ図はそうなっています。

以上から、A-aとC-cが矛盾します。

解答