センター試験 数学I・数学A 2015年度 第2問 [2] 解説
問題編
問題
$\triangle$ABC において、$\mathrm{ AB }=3$、$\mathrm{ BC }=5$、$\angle \mathrm{ ABC }=120^{\circ}$ とする。
このとき、$\mathrm{ AC }=\myBox{オ}$、$\displaystyle \sin\angle \mathrm{ ABC }=\frac{\sqrt{\myBox{カ}} }{\myBox{キ}}$であり、$\displaystyle \sin\angle \mathrm{ BCA }=\frac{\myBox{ク}\sqrt{\myBox{ケ}} }{\myBox{コサ}}$である。
直線BC上に点D を、$\mathrm{ AD }=3\sqrt{3}$ かつ $\angle\mathrm{ ADC }$ が鋭角、となるようにとる。点P を線分BD上の点とし、$\triangle$APC の外接円の半径を R とすると、R のとり得る値の範囲は$\displaystyle \frac{\myBox{シ}}{\myBox{ス}} \leqq R \leqq \myBox{セ}$ である。
考え方
前半は、正弦定理、余弦定理を使って、他の辺の長さなどを求める問題です。
後半は、「外接円の半径」なので正弦定理を使いますが、角度がどう変わるのか考えながら解く必要があります。
解答編
問題
$\triangle$ABC において、$\mathrm{ AB }=3$、$\mathrm{ BC }=5$、$\angle \mathrm{ ABC }=120^{\circ}$ とする。
このとき、$\mathrm{ AC }=\myBox{オ}$、$\displaystyle \sin\angle \mathrm{ ABC }=\frac{\sqrt{\myBox{カ}} }{\myBox{キ}}$であり、$\displaystyle \sin\angle \mathrm{ BCA }=\frac{\myBox{ク}\sqrt{\myBox{ケ}} }{\myBox{コサ}}$である。
解説
図をかくと、次のようになっています。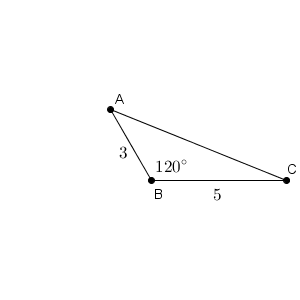
余弦定理から
\begin{eqnarray}
\mathrm{ AC }^2 &=& \mathrm{ AB }^2 + \mathrm{ BC } ^ 2 - 2 \mathrm{ AB } \cdot \mathrm{ BC } \cos \angle \mathrm{ ABC } \\
&=& 3^2 + 5^2 - 2 \cdot 3 \cdot 5 \cdot (-1/2)\\
&=& 9+25+15 = 49\\
\end{eqnarray}よって、ACの長さは7となります。
また、$\angle \mathrm{ ABC }=120^{\circ}$なので、\[ \sin \angle \mathrm{ ABC } = \frac{\sqrt{3} }{2} \]となります。
これらを使うと、正弦定理から、
\begin{eqnarray}
\frac{\mathrm{ AC } }{\sin\angle \mathrm{ ABC } } &=& \frac{\mathrm{ AB } }{\sin\angle \mathrm{ BCA } } \\[5pt]
7 \sin \angle \mathrm{ BCA } &=& 3\cdot \frac{\sqrt{3} }{2} \\[5pt]
\sin \angle \mathrm{ BCA } &=& \frac{ 3\sqrt{3} }{ 14 }
\end{eqnarray}となります。
解答
オ:7カキ:32
クケコサ:3314
解答編 つづき
問題
直線BC上に点D を、$\mathrm{ AD }=3\sqrt{3}$ かつ $\angle\mathrm{ ADC }$ が鋭角、となるようにとる。点P を線分BD上の点とし、$\triangle$APC の外接円の半径を R とすると、R のとり得る値の範囲は$\displaystyle \frac{\myBox{シ}}{\myBox{ス}} \leqq R \leqq \myBox{セ}$ である。
解説
状況は次のようになっています。
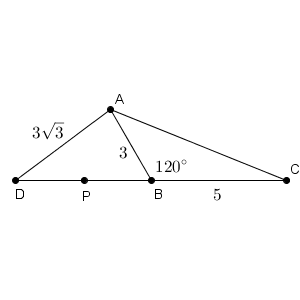
ここで注意しておくことは、三角形APCについて、ACの長さが7であること、$\sin\angle\mathrm{ PCA }$の値がわかっていることです。この2つは、Pが動いても変わりません。これらが利用できるなら、積極的に利用していきたいところです。
まず、「外接円の半径」ときたら、正弦定理です。
\begin{eqnarray}
\frac{\mathrm{ AC } }{\sin\angle \mathrm{ APC } } &=& 2R
\end{eqnarray}
Pが線分BD上を動いたときに、$\angle\mathrm{ APC }$が変わるので、Rも変化するわけですね(分子のACは一定)。
$\angle\mathrm{ APC }$が一番大きい時は、PがBにいるときで120°、一番小さい時は、Dにいるときですね。このときの$\angle\mathrm{ APC }(=\angle\mathrm{ ADC })$の値はわかりませんが、鋭角であることだけはすでにわかっています。
次に、上の式の$\sin\angle\mathrm{ APC }$を考えると、$\angle\mathrm{ APC }$が120°から鋭角に変化していくことから、$\angle\mathrm{ APC }=90^{\circ}$となるときに、$\sin\angle\mathrm{ APC }$が最大になり、Rが最小になることがわかります。この時のRは次のようになります。
\begin{eqnarray}
\frac{\mathrm{ AC } }{\sin 90^\circ} &=& 2R \\
R &=& 7/2
\end{eqnarray}これが、Rの最小値となります。
一方、Rが最大になるとき、つまり、$\sin\angle\mathrm{ APC }$が最小になるときを考えましょう。こうなる候補としては、$\angle\mathrm{ APC }$が120°の時か$\angle\mathrm{ ADC }$の時しかありません。まず、120°のときは次のようになります。
\begin{eqnarray} \frac{\mathrm{ AC } }{\sin 120^\circ} &=& 2R \\ R &=& \frac{7}{2 \cdot \frac{\sqrt{3} }{2} } \\ &=& \frac{7\sqrt{3} }{3} \end{eqnarray}次に、$\angle\mathrm{ APC }$が$\angle\mathrm{ ADC }$の時、つまり、Pが点Dにいるときについて考えてみます。もう一度図を見ておきましょう。

このときも上と同じ正弦定理の式を考えてもいいのですが、$\sin\angle\mathrm{ ADC }$の値がわからないので計算する必要があります。しかし、ADと$\angle\mathrm{ DCA }(=\angle\mathrm{ BCA })$に対して正弦定理を使えば、クケコサの結果も使って、次のように簡単に求められます。
よって、2つの結果を比較すれば、PがDにいるときに、Rは最大値7をとることがわかります。





