センター試験 数学I・数学A 2015年度 第1問 解説

問題編

問題

　2次関数\[ y=-x^2+2x+2 \quad \cdots ① \]のグラフの頂点の座標は $\left(\myBox{ア},\myBox{イ}\right)$である。また\[y=f(x)\]は x の2次関数で、そのグラフは、①のグラフを x軸方向にp、y軸方向にq だけ平行移動したものであるとする。

(1) 下の $\mybox{ウ}$、$\mybox{オ}$ には、次の 0 ～ 4 のうちから当てはまるものを一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　0: $\gt$
　1: $\lt$
　2: $\geqq$
　3: $\leqq$
　4: $\ne$

　$2 \leqq x \leqq 4$における $f(x)$ の最大値が $f(2)$ になるような p の値の範囲は\[ p\ \myBox{ウ}\ \myBox{エ} \]であり、最小値が $f(2)$ になるような p の値の範囲は\[ p\ \myBox{オ}\ \myBox{カ} \]である。

(2) 2次不等式 $f(x) \gt 0$ の解が $-2 \lt x \lt 3$ になるのは\[ p = \frac{\myBox{ケコ}}{\myBox{ク}}, \quad q=\frac{\myBox{コサ}}{\myBox{シ}} \]のときである。

考え方

頂点は平方完成を行うだけですね。

(1)の最大最小の問題は、グラフを描いて、どういう状況になるかを考えると解きやすくなります。

(2)は、まず $f(x)$ の式を求めます。その後に頂点の座標を見比べると解けます。

解答編

問題

　2次関数\[ y=-x^2+2x+2 \quad \cdots ① \]のグラフの頂点の座標は $\left(\myBox{ア},\myBox{イ}\right)$である。

解説

解答

解答編 つづき

問題

また\[y=f(x)\]は x の2次関数で、そのグラフは、①のグラフを x軸方向にp、y軸方向にq だけ平行移動したものであるとする。

(1) 下の $\mybox{ウ}$、$\mybox{オ}$ には、次の 0 ～ 4 のうちから当てはまるものを一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　0: $\gt$
　1: $\lt$
　2: $\geqq$
　3: $\leqq$
　4: $\ne$

　$2 \leqq x \leqq 4$における $f(x)$ の最大値が $f(2)$ になるような p の値の範囲は\[ p\ \myBox{ウ}\ \myBox{エ} \]であり、最小値が $f(2)$ になるような p の値の範囲は\[ p\ \myBox{オ}\ \myBox{カ} \]である。

解説

頂点が $(1,3)$ のグラフを x軸方向に p、y軸方向に q だけ平行移動したものが $y=f(x)$ なので、このグラフの頂点は $(1+p,3+q)$ となります。

このことをふまえ、まずは、 $2 \leqq x \leqq 4$ における $f(x)$ の最大値が $f(2)$ になる場合を求めます。元のグラフが上に凸であることから考えると、区間の左端が最大値になるには、頂点の位置が区間の左端かそれより左にないといけません。下のグラフをみると、グラフがこれより左なら、区間の左端で最大値をとることがわかります。

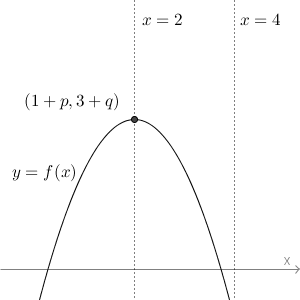
これを式で書くと、$1+p\leqq2$ となるので、$p\leqq1$ であることがわかります。

次に最小値が $f(2)$ になる場合を求めます。最小値になりうるのは、区間の左端か右端です。下のグラフより、最小値が $f(2)$ になるには、頂点の位置が区間の真ん中かそれより右にないといけません。

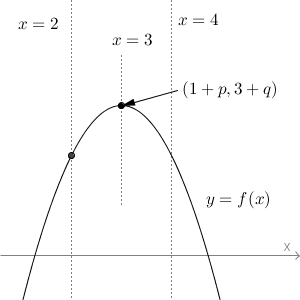
これを式で書くと、$1+p\geqq3$ なので、$p\geqq2$ であることがわかります。

解答

解答編 つづき

問題

(2) 2次不等式 $f(x) \gt 0$ の解が $-2 \lt x \lt 3$ になるのは\[ p = \frac{\myBox{ケコ}}{\myBox{ク}}, \quad q=\frac{\myBox{コサ}}{\myBox{シ}} \]のときである。

解説

$f(x)>0$ の解が、$-2 \lt x \lt 3$ となる場合を求めます。これは、$f(x)=0$ の解が、$x=-2,3$ である、ということです。

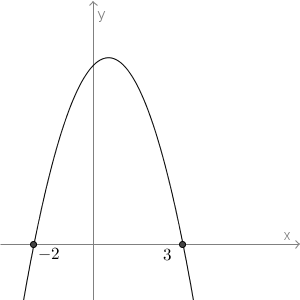
元の2次関数の $x^2$ の係数が $-1$ なので、$f(x)$ は次のようになります。
\begin{eqnarray} f(x) &=& -(x+2)(x-3)\\ &=& -(x^2-x-6)\\ &=& -\left(x^2-x+\frac{1}{4} - \frac{1}{4} -6 \right) \\ &=& -\left(x-\frac{1}{2} \right)^2+ \frac{25}{4} \end{eqnarray}

$y=f(x)$ の頂点が $( 1+p, 3+q )$ であり、上の式から $\displaystyle \left( \frac{1}{2}, \frac{25}{4} \right)$ でもあるので、$p=-\dfrac{1}{2}$, $q=\dfrac{13}{4}$ と求められます。

解答