【標準】複素数の積と回転
ここでは、複素数の積と回転が関連していることを用いて、点の座標を求める問題を考えてみます。
複素数の積と回転
【基本】複素数の極形式と積でも見たように、 $0$ でない複素数 $z_1, z_2$ が
\begin{eqnarray}
z_1 &=& r_1(\cos\theta_1+i\sin\theta_1) \\[5pt]
z_2 &=& r_2(\cos\theta_2+i\sin\theta_2) \\[5pt]
\end{eqnarray}と書けているとき、この2つの積は、\[ z_1z_2=r_1r_2\{ \cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\} \]となるのでした。複素数の積を極形式で表せば、元の複素数の絶対値同士を掛け、偏角を足したものになる、ということです。
このことから、複素数 $z$ に対して $r(\cos\theta+i\sin\theta)$ を掛けたものは、点 $z$ を原点を中心に $r$ 倍し、反時計回りに $\theta$ だけ回転した点に対応することがわかります。このことも、上のリンク先で見た内容です。
このことを利用して、点の座標を求める問題を考えてみましょう。
正三角形の残りの点を複素数を用いて求める
「複素数の積」や「回転」といった言葉は出てきていないのですが、この問題ではこれらを使って考えることができます。「三角形 OAB が正三角形である」ということを、「点 B は、点 O を中心に点 A を60度回転して得られる点だ」と解釈するわけです。なので、「60度の回転」に対応する複素数を掛ければおしまいです。
ちょっと注意が必要なのは、どっちむきの回転なのかは決まってない、という点です。反時計回りなら正の向きに、時計回りなら負の向きになります。どちらも条件を満たします。なので、2種類の掛け算をすることになります。
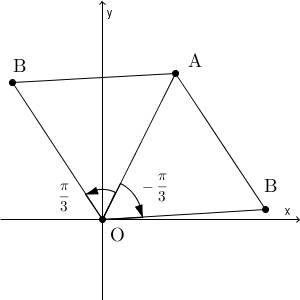
正の向きに回転するほうを先に考えましょう。このときは、 $\cos\dfrac{1}{3}\pi+i\sin\dfrac{1}{3}\pi$ を掛ければいいので、
\begin{eqnarray}
& & (1+2i) \left(\frac{1}{2}+\frac{\sqrt{3} }{2}i\right) \\[5pt]
&=& \frac{1}{2}-\sqrt{3} +\left(1+\frac{\sqrt{3} }{2}\right)i \\[5pt]
\end{eqnarray}となります。
負の向きに回転する場合は、 $-\dfrac{1}{3}\pi$ だけ回転すればいいですね。先ほどの共役複素数を掛ける、と考えてもいいでしょう。 $\dfrac{1}{2}-\dfrac{\sqrt{3} }{2}i$ を掛けて、
\begin{eqnarray}
& & (1+2i) \left(\frac{1}{2}-\frac{\sqrt{3} }{2}i\right) \\[5pt]
&=& \frac{1}{2}+\sqrt{3} +\left(1-\frac{\sqrt{3} }{2}\right)i \\[5pt]
\end{eqnarray}となります。
よって、点 B を表す複素数は
\begin{eqnarray}
& & \frac{1}{2}-\sqrt{3} +\left(1+\frac{\sqrt{3} }{2}\right)i, \\[5pt]
& & \frac{1}{2}+\sqrt{3} +\left(1-\frac{\sqrt{3} }{2}\right)i
\end{eqnarray}となります。
この問題は、次のように出題される可能性もあります。
複素数平面を学ぶ前であれば、線分 OA の垂直二等分線の式を求め、その直線上で $\mathrm{ OB=OA }$ を満たす点を求める、というように解くことになるでしょう。それに比べると、複素数平面上で考えて、上で見たような解き方を使うほうがわかりやすいと思います。回転に対応する複素数を掛ける、というのは、直接的・直感的に座標を求めることができます。
おわりに
ここでは、複素数の積と回転の関係を用いて、三角形の残りの点を求める問題を見ました。ここでは、2点から正三角形の残りの点を求めましたが、例えば、直角二等辺三角形の残りの点、なども同じように求めることもできます。45度回転して $\sqrt{2}$ 倍する、などと考えれば、同じように、対応する複素数を掛けるだけで求められます。
「回転」と書いていなくても、回転だと考え、複素数の積が利用できる場面があることを理解しておきましょう。





