【標準】円に引いた接線の方程式
ここでは、円の外にある点から、円に引いた接線の方程式を求める問題を考えます。
円に引いた接線の方程式
図をかくと、次のようになります。
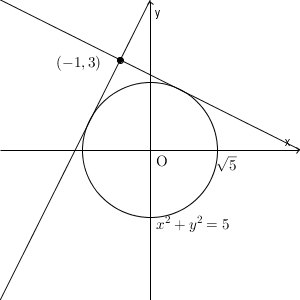
接線の方程式は、【標準】円の接線の方程式(傾き指定)などで見た通り、「円の中心と直線の距離が、半径と一致する」と考えると解きやすいのでしたね。まずはこの方法で考えてみましょう。
円の中心は原点で、半径は $\sqrt{5}$ である、ということはすぐにわかります。ただ、距離を求めるのに必要な、直線の方程式が少しやっかいです。
$(-1,3)$ を通り、 y 軸に平行な直線は、原点からの距離が $1$ なので、この円の接線にはなりません。そのため、円の接線の傾きを m とおくことができます。このとき、接線の方程式は
\begin{eqnarray}
y-3 &=& m(x+1) \\
mx-y+m+3 &=& 0 \\
\end{eqnarray}と書けます。
これより、「円の中心と直線の距離が、半径と一致する」という条件を式で表すと
\begin{eqnarray}
\frac{|m+3|}{\sqrt{m^2+(-1)^2} } &=& \sqrt{5} \\[5pt]
|m+3| &=& \sqrt{5m^2+5} \\[5pt]
\end{eqnarray}となります。両辺は正なので、2乗して
\begin{eqnarray}
m^2+6m+9 &=& 5m^2+5 \\[5pt]
4m^2-6m-4 &=& 0 \\[5pt]
(2m+1)(m-2) &=& 0 \\[5pt]
m &=& 2,-\frac{1}{2}
\end{eqnarray}と求められます。
これらを直線の方程式に代入して、接線の方程式は\[ y=2x+5,\ y=-\frac{1}{2}x+\frac{5}{2} \]と求められます。
直線の方程式が少し複雑になってしまいますが、上のように、円の中心と直線との距離が、円の半径と一致することを利用して、解くことができます。
円に引いた接線の方程式その2
先ほどの例題は、「 $(-1,3)$ を通る直線が、円に接する」という考え方で解いたことになります。ただ、別の切り口として、「円の接線が $(-1,3)$ を通る」という考え方もあります。この方法でも解いてみましょう。
使うのは、【基本】円の接線の方程式で紹介した、接線の方程式です。次のような内容でした。
ここで注意が必要なのは、この公式を使う場合、「接点の座標」が必要な点です。これは今の時点ではわかりません。なので、これを文字で置いて、考えていきましょう。
接点の座標を $(x_1,y_1)$ とすると、この円の接線の方程式は\[ x_1x+y_1y=5 \]となります。これが $(-1,3)$ を通ることから
\begin{eqnarray}
-x_1+3y_1 &=& 5 \\
x_1 &=& 3y_1-5 \\
\end{eqnarray}が成り立ちます。
また、接点は円周上の点でもあることから
\begin{eqnarray}
x_1^2+y_1^2=5
\end{eqnarray}も成り立ちます。
1つ目の式を2つ目の式に代入して
\begin{eqnarray}
(3y_1-5)^2+y_1^2 &=& 5 \\[5pt]
9y_1^2 -30y_1 +25 +y_1^2 &=& 5 \\[5pt]
10y_1^2 -30y_1 +20 &=& 0 \\[5pt]
y_1^2 -3y_1 +2 &=& 0 \\[5pt]
(y_1-1)(y_1-2) &=& 0 \\[5pt]
y_1 &=& 1,2
\end{eqnarray}が得られます。直線の方程式に代入すると、接点の座標は $(-2,1)$, $(1,2)$ となることがわかります。これらを接線の公式に代入して\[ -2x+y=5, \ x+2y=5 \]が求める接線の方程式となります。見た目は違いますが、変形すれば同じ式を表していることがわかります。
おわりに
ここでは、外部の点から円に引いた接線の方程式について考えました。
「外部の点から円に引いた接線」は、「外部の点を通る直線が円に接する」と考えても、「接線が外部の点を通る」と考えても解くことができます。計算量的にはあまり変わりませんが、後者の解き方で使った、「接点を文字で置いて考える」という方法は大事です。こうすることで、接線の方程式が簡単に表せるようになるからです。よく理解しておきましょう。





