【標準】2つの円が交わる条件

ここでは、2つの円が交わる条件を求める問題を見ていきます。

2つの円が交わる条件

1つ目の円の半径が決まっていませんが、図をかくとだいたいこんな感じになります。

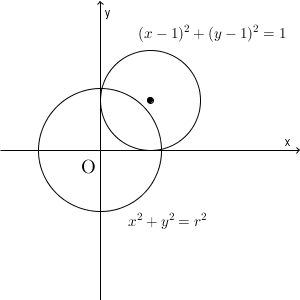
まず、(1)から考えましょう。1つ目の円の中心（＝原点）は2つ目の円の外にあるので、2つ目の円の内側で1つ目と円と接する、ということはありません。そのため、内接するときは、「1つ目の円の内側で2つ目の円と接する」場合となります。

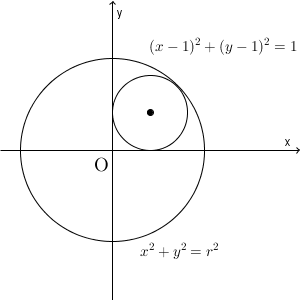
このときの半径を求めましょう。

【基本】2つの円の共有点（中心間の距離に注目）で見た通り、共有点の個数を考えるには、中心間の距離を考えればいいんでしたね。わかりやすいように、上の図に中心間をつないだ直線を追加してみましょう。

図からもわかる通り、1つ目の円の半径は、2つ目の円の半径と中心間の距離の和になっています。2つ目の円の半径は $1$ で、中心間の距離は $\sqrt{1^2+1^2}=\sqrt{2}$ なので、内接するときの半径は\[ r=1+\sqrt{2} \]と求めることができます。

続いて、(2)について考えてみましょう。

(1)で求めた半径より大きい場合、2つ目の円は1つ目の円の内側に含まれるため、共有点を持つことはありません。一方、(1)で求めた半径より小さくすると、しばらくの間は共有点が2点となります。

しかし、さらに小さくしていくと、外接するようになり、共有点は1点になります。1つ目の円が小さくなるので、少し図を拡大しています。

そして、さらに r を小さくすると、共有点はなくなります。

そのため、共有点が2点となるのは、内接するときと外接するときの間（内接・外接するときを除く）であることがわかります。

内接するときの半径は、(1)で求めた通り $1+\sqrt{2}$ でしたね。外接するときの半径を求めましょう。

外接するとき、2つの円の半径の和が、2つの円の中心間の距離となっていますね。このことから、このときの1つ目の円の半径は\[ \sqrt{2}-1 \]となることがわかります。

以上から、2つの円が異なる2つの共有点を持つ条件は\[ \sqrt{2}-1 \lt r \lt \sqrt{2}+1 \]となることがわかります。

おわりに

ここでは、2つの円が交わる条件を求める問題を見てきました。2つの異なる共有点を持つ条件を求めるには、内接するとき・外接するときを基準に考えて解きます。また、内接するとき・外接するときの半径を求めるには、2つの円の中心間の距離と接点との位置関係から考えるようにします。

共有点の座標を求める必要がない場合には、中心間の距離に注目して解くと、解きやすいです。