🏠 Home / 数学II / 図形と方程式 / 円と方程式

【標準】ある直線とx軸とy軸に接する円の方程式

🕒 2017/08/18 🔄 2023/05/01

ここでは、x 軸と y 軸、そして、もう1本の直線に接する円の方程式を見ていきます。

📘 目次

x軸とy軸に接する円

まず、 x 軸と y 軸の両方に接する円とはどういうものか、見てみましょう。

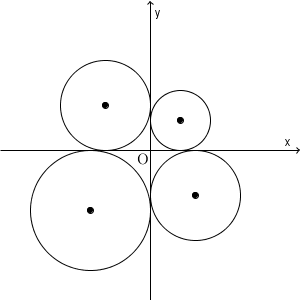
円の場所は、右上、右下、左上、左下の4パターンが考えられますね。ここで、中心と接点との結んでみましょう。

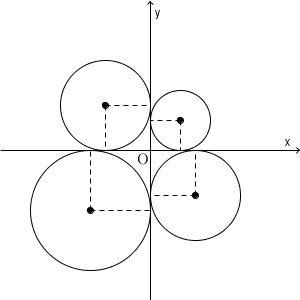
そうすると、円の中心と原点と接点を使ってできる四角形は、正方形になりますね。つまり、中心の x 座標・ y 座標の絶対値は、半径と一致します。

この性質はとても重要です。「ある円が、 x 軸と y 軸の両方に接する」ということがわかった時点で、中心の座標は半径を使って書けるわけです。ということは、半径さえ求めれば、あとは解けたも同然ですね。

このことを踏まえて、次の例題を解いてみましょう。

ある直線とx軸とy軸に接する円

例題

x 軸、 y 軸、直線 $3x+4y-12=0$ のすべてに接する円の方程式を求めなさい。

【基本】円の接線の方程式や【標準】円の接線の方程式（傾き指定）では、円から接線を求めましたが、この問題では接線から円を求めます。

まずは、図をかいてみましょう。

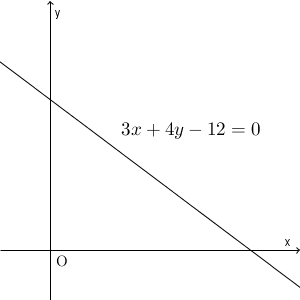
図から、円は、右上の部分にあることがわかりますね。この3つの直線で囲まれた部分の中に、3直線に接する円ができそうだ、というのはわかりますね。方程式を考えてみましょう。

先ほど考えた通り、半径を使えば円の方程式を表すことができます。求める円の半径を $r(\gt 0)$ とすると、中心の座標は $(r,r)$ と書けます。よって、円の方程式は\[ (x-r)^2+(y-r)^2=r^2 \]となります。 r を求めれば終わりですね。

中心が $(r,r)$ と書けるのは、この円が x 軸と y 軸に接することからわかったことですね。まだ、直線 $3x+4y-12=0$ に接することを考えていません。この直線について考えてみましょう。

円と直線が接する、というのは、直線の方程式を円の方程式に代入し、判別式が $0$ になる条件を求める、という流れでも得られます。しかし、【標準】円の接線の方程式（傾き指定）でも見た通り、中心と直線との距離を見たほうが計算が簡単になることが多いので、こちらを使ってみましょう。

中心 $(r,r)$ と直線 $3x+4y-12=0$ との距離は
\begin{eqnarray} \frac{|3r+4r-12|}{\sqrt{3^2+4^2} }=\frac{|7r-12|}{5} \end{eqnarray}となります。これが、半径 r と一致することから \begin{eqnarray} \frac{|7r-12|}{5} &=& r \\[5pt] |7r-12| &=& 5r \\[5pt] 7r-12 &=& \pm 5r \\[5pt] \end{eqnarray}となります。これを解いて、\[ r=6,1 \]が得られます。どちらも正なので、どちらも解となります。

これより、求める円の方程式は
\begin{eqnarray} (x-6)^2+(y-6)^2 &=& 36 \\ (x-1)^2+(y-1)^2 &=& 1 \end{eqnarray}となります。図をかくと、こうなります。