【標準】微分可能な関数の係数を求める
ここでは、ある関数が微分可能となるように係数を決める問題を見ていきます。
微分可能な関数の係数を求める
\begin{eqnarray} f(x) = \begin{cases} ax^2 & ( x \lt 1 ) \\ x+b & ( x \geqq 1 ) \end{cases} \end{eqnarray}
$f(x)$ は $x=1$ を境目にして、性質が変わっています。そのため、微分可能であるかどうかは、すぐにはわかりません。微分の定義に戻って確かめることになります。
定義に戻ると(参考:【基本】微分係数と導関数(の復習))\[ \lim_{h\to 0}\frac{f(1+h)-f(1)}{h} \]が存在するかどうかを考えればいいですね。この極限を、 $h\to +0$ としたときと $h\to -0$ としたとき、つまり、大きい方から近づけたときと小さい方から近づけたときで、同じ有限の値になるかどうかを見ればいいんですね。
ただ、これだと条件式が1つしか出てきません。わからないものが2つあるので、条件式は2つ必要です。
そこで使えるのが、「微分可能なら連続である」という条件です(参考:【基本】微分可能性と連続性)。これより、\[ \lim_{x\to 1} f(x)=f(1) \]という条件も出てきます。これで、式が2つできます。これらを用いて計算できるか、やってみましょう。
まず、 $x=1$ での連続性を考えましょう。\[ f(1)=1+b \]となります。 $\lim_{x\to 1+0}f(x)=f(1)$ が成り立つことはすぐにわかります。そこで、 $x\to 1-0$ としたときの極限を考えましょう。 $x\lt 1$ のときは $f(x)=ax^2$ なので、\[ \lim_{x\to 1-0} f(x)=a \]となります。右側極限も左側極限も同じでないといけないので、\[ a=b+1 \]という条件が得られます。
続いて、微分係数について考えましょう。まずは $h\to +0$ のときを計算すると
\begin{eqnarray}
& &
\lim_{h\to +0} \frac{f(1+h)-f(1)}{h} \\[5pt]
&=&
\lim_{h\to +0} \frac{(1+h+b)-(1+b)}{h} \\[5pt]
&=&
1
\end{eqnarray}となります。また、 $h\to -0$ のときは
\begin{eqnarray}
& &
\lim_{h\to -0} \frac{f(1+h)-f(1)}{h} \\[5pt]
&=&
\lim_{h\to -0} \frac{a(1+h)^2-(1+b)}{h} \\[5pt]
\end{eqnarray}となります。ここで、先ほど見た通り、連続性から $a=b+1$ が得られていたので、この極限は
\begin{eqnarray}
& &
\lim_{h\to -0} \frac{a(1+h)^2-a}{h} \\[5pt]
&=&
\lim_{h\to -0} \frac{2ah+ah^2}{h} \\[5pt]
&=&
2a
\end{eqnarray}となります。両側極限が等しいことから、\[ a=\frac{1}{2} \]が得られ、 $b=a-1$ なので、\[ b=-\frac{1}{2} \]であることがわかります。これが答えです。
ちなみに、このときの $y=f(x)$ のグラフは次のようになります。
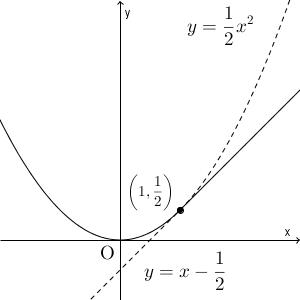
$x=1$ の前後で関数の性質が変わっていますが、グラフはつながっている(連続である)ことがわかり、とがらずになめらかに変化していることがわかります。
おわりに
ここでは、微分可能な関数の係数を求める問題を見ました。今まで見てきたように、整式で表される関数や無理関数、分数関数は微分可能でしたが、この例題のように、途中で式が切り替わってしまうような関数は、定義通りに考える必要があります。





