【標準】定積分を使って不等式を示す

🕒 2018/12/30 🔄 2023/05/01

ここでは、定積分を使って不等式を示す問題を見ていきます。

📘 目次

定積分を使って不等式を示すその１

例題1

$0\leqq x\leqq \dfrac{\pi}{2}$ のときに $\dfrac{2}{\pi}x \leqq \sin x \leqq x$ が成り立つことを利用して、次の不等式を示しなさい。\[ \frac{\pi}{2}(e-1)\lt \int_0^{\frac{\pi}{2} } e^{\sin x}dx \lt e^{\frac{\pi}{2} }-1 \]

定積分を直接求めることは難しいので、値を求めることなく不等式を示す方法を考えましょう。【基本】定積分を使って不等式を示すの後半で見たように、 $f(x)\geqq g(x)$ なら\[ \int_a^b f(x)dx \geqq \int_a^b g(x)dx \]が成り立つことを利用します。

使う関係式が書かれているから簡単ですね。 $0\leqq x\leqq \dfrac{\pi}{2}$ のときに $\dfrac{2}{\pi}x \leqq \sin x \leqq x$ が成り立つことから\[ e^{\frac{2}{\pi}x} \leqq e^{\sin x}\leqq e^x \]が成り立ちます。また、「つねに等号が成り立つ」わけではないことから、各辺を $0$ から $\dfrac{\pi}{2}$ まで積分すると、\[ \int_0^{\frac{\pi}{2} } e^{\frac{2}{\pi}x}dx \lt \int_0^{\frac{\pi}{2} } e^{\sin x}dx \lt \int_0^{\frac{\pi}{2} } e^x \]が成り立つことがわかります（イコールがなくなっている点に注意しましょう）。また、
\begin{eqnarray} & & \int_0^{\frac{\pi}{2} } e^{\frac{2}{\pi}x}dx \\[5pt] &=& \Big[ \frac{\pi}{2} e^{\frac{2}{\pi}x} \Big]_0^{\frac{\pi}{2} } \\[5pt] &=& \frac{\pi}{2} (e-1) \\[5pt] \end{eqnarray}であり、 \begin{eqnarray} & & \int_0^{\frac{\pi}{2} } e^xdx \\[5pt] &=& \Big[ e^x \Big]_0^{\frac{\pi}{2} } \\[5pt] &=& e^\frac{\pi}{2}-1 \\[5pt] \end{eqnarray}であることから、\[ \frac{\pi}{2}(e-1)\lt \int_0^{\frac{\pi}{2} } e^{\sin x}dx \lt e^{\frac{\pi}{2} }-1 \]となることがわかります。

ちなみに、条件にあった「 $0\leqq x\leqq \dfrac{\pi}{2}$ のときに $\dfrac{2}{\pi}x \leqq \sin x \leqq x$ が成り立つ」というのは、次の図を見てみるとわかるでしょう。 $y=x$ というのは、 $y=\sin x$ の $x=0$ での接線です。

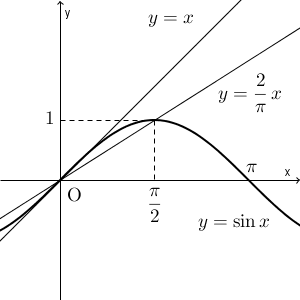
きちんと示すには、 $f(x)=x-\sin x$, $g(x)=\sin x-\dfrac{2}{\pi}x$ とおいて、増減表をかいて考えればいいでしょう。

定積分を使って不等式を示すその２

例題2

次の不等式を示しなさい。ただし、 $n$ は3以上の整数とします。\[ \frac{1}{2}\lt \int_0^{\frac{1}{2} } \frac{1}{\sqrt{1-x^n} }dx \lt\frac{\pi}{6} \]

今度も定積分の入った不等式です。定積分を計算するのは難しいので先ほどと同じ手法を使いましょう。

不等式の左側と右側を積分の形にしないといけません。また、 $0\leqq x\leqq \dfrac{1}{2}$ の範囲で、大小関係がはっきりわかっているもので表さないといけません。左側については、\[ 1\leqq \dfrac{1}{\sqrt{1-x^n} } \]が成り立つことと、左辺の積分が $\dfrac{1}{2}$ となることから、 $1$ という関数を考えればいいことがわかります。

$n$ が3以上の整数であることから、右側の不等式を示すためには、\[ \frac{1}{\sqrt{1-x^n} }\lt \frac{1}{\sqrt{1-x^2} } \]を使うのではないか、と予想できます。この右辺の積分は、少し計算が難しいですが、 $x=\sin t$ と置いて置換積分を使いましょう（参考：【標準】定積分の置換積分（三角関数：cosθやsinθを使う））。
\begin{eqnarray} & & \int_0^{\frac{1}{2} } \frac{1}{\sqrt{1-x^2} } dx \\[5pt] &=& \int_0^{\frac{\pi}{6} } \frac{1}{\cos t} \cdot \cos t dt \\[5pt] &=& \Big[ \ t\ \Big]_0^{\frac{\pi}{6} } \\[5pt] &=& \frac{\pi}{6} \end{eqnarray}となります。

以上のことを踏まえると、次のようにして不等式を示すことができます。まず、 $0\leqq x\leqq \dfrac{1}{2}$ の範囲では\[ 1\leqq \frac{1}{\sqrt{1-x^n} } \lt \frac{1}{\sqrt{1-x^2} } \]が成り立ちます。また、この範囲で「つねに等号が成り立つ」ことはないので、 $0$ から $\dfrac{1}{2}$ まで積分して\[ \int_0^{\frac{1}{2} }dx \lt \int_0^{\frac{1}{2} } \frac{1}{\sqrt{1-x^n} }dx \lt \int_0^{\frac{1}{2} }\frac{1}{\sqrt{1-x^2} }dx \]が成り立ちます。イコールがなくなっている点に注意しましょう。積分区間内で一致しているわけではないので、積分した値がイコールになることはありません。さらに、左側・右側の積分を計算して\[ \frac{1}{2}\lt \int_0^{\frac{1}{2} } \frac{1}{\sqrt{1-x^n} }dx \lt\frac{\pi}{6} \]が成り立つことがわかります。これで示すことができました。