【応用】複素数の積と回転
ここでは、原点以外の点を中心に回転したときに、ある点がどの点に移動するかを求める問題を見ていきます。
三角形の残りの点を複素数を用いて求める
図でいうと、こういう状況です。
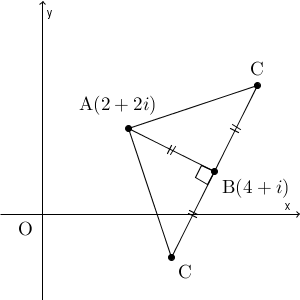
【標準】複素数の積と回転で見たように、三角形の残りの点を「回転によって得られる点」と考えれば、複素数の積が利用できます。今の問題であれば、 $\mathrm{ AC }=\sqrt{2}\mathrm{ AB }$ なのだから、\[ \sqrt{2} \left\{ \cos\left(\pm\frac{\pi}{4}\right)+i\sin\left(\pm\frac{\pi}{4}\right) \right\} \]を掛ければよさそうだ、と考えられます(複号同順)。ただし、単純に掛けるだけでは答えは得られません。
複素数の積は回転と関連していますが、この回転はつねに原点が中心となります。しかし、今の場合は、点A を中心に回転しなければなりません。なので、点 B に先ほどの複素数を掛けるだけではダメなんですね。
ではどうすればいいでしょうか。複素数の積は、原点を中心とした回転にしか対応していないので、中心を原点に移すことを考えましょう。
まず、①点 A が原点に来るように平行移動してから考えます。そうして、②原点を中心に、点 B を $\sqrt{2}$ 倍・45度回転してから、③先ほどとは逆の平行移動をする。こうすることで、点 C が得られます。次の図は、正の向きに回転する場合を表しています。

複素数の積は、原点を中心とした回転にしか対応していないので、少し面倒に思えますが、このようにすれば計算することができます。
では、まず、平行移動をしてみましょう。点 A が原点にくるように平行移動したとき、点 B は、\[ (4+i)-(2+2i)=2-i \]となります。つぎに、拡大・回転を考えましょう。長さは $\sqrt{2}$ 倍すればいいですね。正の向きに $\dfrac{\pi}{4}$ だけ回転する場合を考えると、拡大・回転後の点は
\begin{eqnarray}
& & (2-i)\times\sqrt{2} \left(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\right) \\[5pt]
&=& (2-i)\times(1+i) \\[5pt]
&=& 3+i \\[5pt]
\end{eqnarray}となります。負の向きに回転した場合は
\begin{eqnarray}
& & (2-i)\times\sqrt{2} \left(\cos\frac{-\pi}{4}+i\sin\frac{-\pi}{4}\right) \\[5pt]
&=& (2-i)\times(1-i) \\[5pt]
&=& 1-3i \\[5pt]
\end{eqnarray}となります。
そして、この2点を、元の位置に戻るように平行移動すればおしまいです。原点が点 A に移動するように平行移動すると、それぞれの点は
\begin{eqnarray}
(3+i)+(2+2i) &=& 5+3i \\[5pt]
(1-3i)+(2+2i) &=& 3-i \\[5pt]
\end{eqnarray}となります。よって、 $5+3i$, $3-i$ が答えとなります。

上のように、目盛りを追加すると、わかりやすいですね。直接長さを求めることで、たしかに直角二等辺三角形になっていることが確かめられます(3辺の長さが $\sqrt{5}$, $\sqrt{5}$, $\sqrt{10}$ の三角形なので)。
一般の場合
一般的な場合を使って、もう一度流れを見ておきましょう。
点 $\alpha$ を中心に、点 $\beta$ を角 $\theta$ だけ回転したときに、点 $\gamma$ に移るとしましょう。このとき、 $\gamma$ がどのように表されるかを求めてみます。
先ほどと同じように、点 $\alpha$ が原点にくるように平行移動しましょう。そうすると、点 $\beta$ は $\beta-\alpha$ に移動し、点 $\gamma$ は $\gamma-\alpha$ に移動します。こうすれば、原点を中心とした回転を考えることができます。
原点を中心に、点 $\beta-\alpha$ を角 $\theta$ だけ回転すると、点 $\gamma-\alpha$ に移るのだから、次の式が成り立ちます。\[ \gamma-\alpha=(\beta-\alpha)(\cos\theta+i\sin\theta) \]よって、 $\gamma$ は\[ \gamma=(\beta-\alpha)(\cos\theta+i\sin\theta)+\alpha \]と書くことができます。一般的には、このような形で求めることができます。
これは、公式として覚えるというよりも、「回転の軸を原点に移してから考えればいい」ということを理解しておくのがいいでしょう。
おわりに
ここでは、複素数の積と回転の関係を用いて点の座標を求める問題を考えました。回転の中心が原点ではない場合でしたが、こういう場合でも、原点での中心が使えるように、事前に平行移動をしておけばいい、ということを理解しておきましょう。





