【応用】2つの円の共通接線の方程式

🕒 2017/08/30 🔄 2023/05/01

ここでは、2つの円の共通接線の方程式を求める問題を考えていきます。

📘 目次

2つの円の共通接線の方程式

例題

円 $x^2+y^2=9$ と円 $(x-10)^2+y^2=9$ の共通接線の方程式を求めなさい。

共通接線とは、どちらの図形にも接する直線のことです。円の場合、中心間の距離と半径との関係によって、本数が変わってくるのでしたね（参考：【基本】2つの円の共有点（中心間の距離に注目））。今の場合、2つとも半径は $3$ で、中心間の距離が $10$ なので、共通接線の数は4本となります。

実際に図をかいてみると、次のようになります。

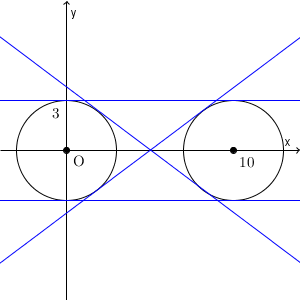
この問題では、図から考えることもできるのですが、ここでは計算で求める方法を考えていきましょう。

接線の方程式を求めるアプローチはいくつかありました。【基本】円の接線の方程式で見た、円の接線の方程式の公式を用いる方法が1つ。また、【標準】円の接線の方程式（傾き指定）で見たように、円の中心と接線との距離が半径と一致する、と考える方法もあります。【標準】円に引いた接線の方程式で見たように、どちらでも解ける場合もあります。

今回のような共通接線の場合は、以下のように、2つの方法を組み合わせて解くのがいいと思います。

まずは、円 $x^2+y^2=9$ 上の接点の座標を $(p,q)$ とおきます。円周上の点なので、\[ p^2+q^2=9 \]が成り立ちます。また、この点での接線の方程式は、【基本】円の接線の方程式で見た公式から、\[ px+qy=9 \]となります。

この接線が、もう1つの円に接する、と考えます。そうすると、中心 $(10,0)$ からの距離が $3$ なので、【標準】点と直線との距離で見た公式から\[ \frac{|10p-9|}{\sqrt{p^2+q^2} }=3 \]が成り立ちます。 $(p,q)$ が円 $x^2+y^2=9$ 上の点だから、よく見ると、左辺の分母は値がわかります。
\begin{eqnarray} \frac{|10p-9|}{\sqrt{9} } &=& 3 \\[5pt] |10p-9| &=& 9 \\[5pt] 10p-9 &=& \pm 9 \\[5pt] p &=& 0,\frac{9}{5} \\[5pt] \end{eqnarray}となります。

$p=0$ のとき、 $q^2=9$ から $q=\pm3$ が得られます。接線の方程式は $px+qy=9$ で得られるので、\[ y=3,y=-3 \]が得られます。

また、 $p=\dfrac{9}{5}$ のときは\[ q^2=9-\frac{81}{25}=\frac{12^2}{5^2} \]なので、 $q=\pm\dfrac{12}{5}$ が得られます。よって\[ \frac{9}{5}x\pm\frac{12}{5}y=9 \]となります。変形すると\[ 3x+4y=15, 3x-4y=15 \]となります。

以上から、4本の共通接線の方程式は、 $y=3$, $y=-3$, $3x+4y=15$, $3x-4y=15$ となります。

図から、 $y=\pm3$ はすぐにわかるので、確かにこれが共通接線であることがわかりますね。また、次のように線を引けば、 $(5,0)$ を通ることと、接線の傾きが $\pm\dfrac{3}{4}$ であることもわかります。

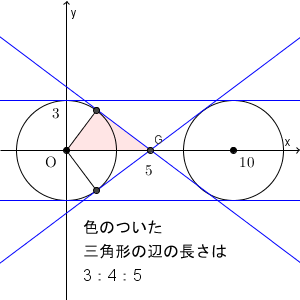
上の解き方では、まず接点を文字で置いて接線を表し、それがもう1つの円に接する、と考えました。もし、接線を $y=ax+b$ などとおいて計算していくと、点と直線との距離の公式が2回出てきます。\[ \frac{|b|}{\sqrt{a^2+1} }=3, \frac{|10a+b|}{\sqrt{a^2+1} }=3 \]この2つの式から
\begin{eqnarray} |10a+b| &=& |b| \\ 10a+b &=& \pm b \\ a &=& 0,-\frac{b}{5} \\ \end{eqnarray}$a=0$ のときは、点と直線との距離の1つ目から $|b|=3$ なので、 $b=\pm 3$ が得られます。また、 $a=-\dfrac{b}{5}$ のときは \begin{eqnarray} |b| &=& 3\sqrt{\frac{b^2}{25}+1} \\[5pt] \end{eqnarray}なので、両辺を2乗して（両辺とも正なので2乗してよい）、計算していくことになります。

どちらでも同じ結論が得られますが、はじめの解き方のほうが、計算はスムーズになるように思います。