【基本】円の接線の方程式

🕒 2017/08/08 🔄 2023/05/01

円と直線の位置関係で、一番特徴的なのは接するときです。ここでは、円の接線の方程式について考えていきます。

📘 目次

原点を中心とする円の接線の方程式

円 $x^2+y^2=r^2$ に接する直線、つまり、接線の方程式について考えましょう。

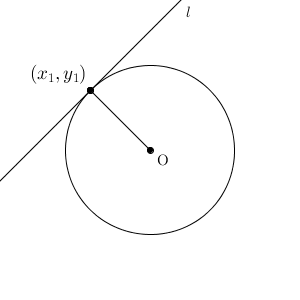
接線は何本でも引けますが、接点を決めれば接線は1本に決まります。ここでは、接点を $(x_1,y_1)$ としましょう。これは円周上の点でもあるので\[ x_1^2+y_1^2=r^2 \]が成り立ちます。

接線も接点を通ります。また、接線の傾きは、円の中心と接線を結んだ線と接線とが垂直に交わることから求めることができます。接点が x 軸・ y 軸上にない場合、円の中心と接点を結んだ線の傾きは $\dfrac{y_1}{x_1}$ なので、接線の傾きは\[ -\frac{x_1}{y_1} \]となります（参考：【基本】垂直な直線の方程式）。

傾きと通る点が分かったので、接線の方程式は
\begin{eqnarray} y-y_1 &=& -\frac{x_1}{y_1}(x-x_1) \\[5pt] y_1y-y_1^2 &=& -x_1x+x_1^2 \\[5pt] x_1x+y_1y &=& y_1^2+x_1^2 \\[5pt] \end{eqnarray}となります。先ほど見たように、接点が円周上にあることから\[ x_1^2+y_1^2=r^2 \]となることを使うと、接線の方程式は\[ x_1x+y_1y=r^2 \]となります。

接点が x 軸上にある場合、接点が $(r,0)$ のときは接線が $x=r$ 、接点が $(-r,0)$ のときは接線が $x=-r$ となり、上の式に含まれています。接点が y 軸上にあるときも、同様に上の式に含まれています。

以上から、次のようにまとめられます。

円の接線の方程式

円 $x^2+y^2=r^2$ 上の点 $(x_1,y_1)$ におけるこの円の接線の方程式は、次で表すことができる。\[ x_1x+y_1y=r^2 \]

円の方程式内の x, y が、1つずつ $x_1,y_1$ に変わっています。形が似ていますね。

例えば、 $x^2+y^2=25$ 上の $(3,-4)$ での接線は、上の公式から\[ 3x-4y=25 \]と求められます。簡単ですね。

実際、この接線の方程式を変形した $y=\dfrac{3x-25}{4}$ を円の方程式に入れてみると
\begin{eqnarray} x^2 +\left(\frac{3x-25}{4}\right)^2 &=& 25 \\[5pt] 16x^2 +(9x^2-150x+625) &=& 400 \\[5pt] 25x^2 -150x+225 &=& 0 \\[5pt] x^2 -6x+9 &=& 0 \\[5pt] (x-3)^2 &=& 0 \\[5pt] \end{eqnarray}となり、 $x=3$ という重解を持つことがわかります。よって、 $(3,-4)$ を接点とする接線であることがわかります。

中心が原点でない場合

先ほど見た例は、原点を中心とする円でしたが、それ以外の円について考えたいこともあります。

円 $(x-a)^2+(y-b)^2=r^2$ 上の点 $(x_1,y_1)$ における接線について、上と対応させながら考えていきましょう。

通る点（＝接点）が分かっているので、傾きを求めればいいですね。上と同様に考えると、接線の傾きは\[ -\frac{x_1-a}{y_1-b} \]となります。このことから、接線の方程式は
\begin{eqnarray} y-y_1 &=& -\frac{x_1-a}{y_1-b} (x-x_1) \\[5pt] (x_1-a)(x-x_1)+(y_1-b)(y-y_1) &=& 0 \\[5pt] \end{eqnarray}となります。

これでもいいのですが、普通は、接点の座標を円の方程式に代入した式\[ (x_1-a)^2+(y_1-b)^2=r^2 \]を足して、左辺をさらにわかりやすくします。計算すると
\begin{eqnarray} & & (x_1-a)(x-x_1)+(x_1-a)^2 \\ & & +(y_1-b)(y-y_1)+(y_1-b)^2 = r^2 \\[5pt] & & (x_1-a)(x-x_1+x_1-a) \\ & & +(y_1-b)(y-y_1+y_1-b)^2 = r^2 \\[5pt] & & (x_1-a)(x-a)+(y_1-b)(y-b)=r^2 \end{eqnarray}となります。こうすると、中心が原点のときとおなじように、円の方程式の $x,y$ に、1つずつ $x_1,y_1$ を代入した式になっています。そのため、こちらの式を使うことが多いです。

円の接線の方程式

円 $(x-a)^2+(y-b)^2=r^2$ 上の点 $(x_1,y_1)$ におけるこの線の接線の方程式は、次で表すことができる。\[ (x_1-a)(x-a)+(y_1-b)(y-b)=r^2 \]

平行移動の考え方に慣れているなら、そちらを使ってもいいでしょう。中心が原点に来るように平行移動すれば、円の方程式は $x^2+y^2=r^2$ となり、接点は $(x_1-a,y_1-b)$ となります。よって、平行移動した後の円に関する接線の方程式は\[ (x_1-a)x+(y_1-b)y=r^2 \]となります。これを元に戻すように平行移動すれば、接線の方程式は\[ (x_1-a)(x-a)+(y_1-b)(y-b)=r^2 \]となり、同じ結果が得られます。