【基本】微分可能性と連続性
ここでは、微分可能であることと連続であることの関係性について見ていきます。
微分可能でない関数
【基本】微分係数と導関数(の復習)では、微分係数や導関数などについて復習をしました。このとき、 $x=a$ で微分係数が存在する場合は、 $x=a$ で微分可能と言う、という話を書きました。
「微分可能」という言葉があるくらいなので、微分できないものもあるということですね。数学IIで学んだ微分では、主に三次関数の微分を考えていたため、微分できないものが登場しませんでしたが、それは運がよかっただけです。世の中には微分できない関数はたくさんあります(人工的にいくらでも作り出すことができます)。
微分できない典型的な関数の例は、 $f(x)=|x|$ です。この関数のグラフは次のようになります。
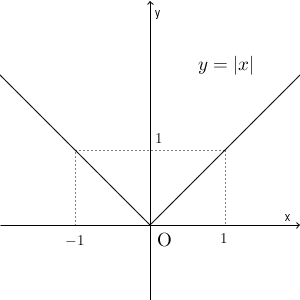
この関数の $x=0$ での微分係数を考えてみましょう。
$x=0$ での微分係数を求めるには、【基本】微分係数と導関数(の復習)でも見た通り、次の極限を求めればいいんでしたね。\[ \lim_{h\to 0} \frac{f(0+h)-f(0)}{h} \]
まず、 $f(0)=|0|=0$ です。また、 $h\to +0$ のとき、 $f(0+h)=|h|=h$ なので、\[ \lim_{h\to +0} \frac{f(0+h)-f(0)}{h}=1 \]となります。 $h\to -0$ のときは、 $f(0+h)=|h|=-h$ なので、\[ \lim_{h\to -0} \frac{f(0+h)-f(0)}{h}=-1 \]となり、2つの極限値が一致しないので、 $h\to 0$ としたときの極限は存在しません。つまり、 $f(x)=|x|$ は $x=0$ で微分できない、ということがわかります。
基本的に、微分可能かどうかは、定義に戻って、微分係数が存在するかどうか(極限が存在するかどうか)を調べることになります。
微分可能かどうか、直感的に判断するには、「微分係数が接線の傾きを表している」ことを利用することができます。 $f(x)=|x|$ のグラフは、 $x=0$ のところでとがっており、接線がひけないことから、微分可能ではないと考えられます。ただ、これはあくまでも予想です。厳密には、微分係数が存在するかどうかを調べて確かめます。
微分可能性と連続性
$f(x)=|x|$ は $x=0$ で微分可能でない、ということを先ほど見ましたが、グラフを見てもわかる通り、この関数は連続であることがわかります。関数が連続であるとは、【基本】関数の連続性や【基本】連続関数で見た通り\[ \lim_{x\to a}f(x)=f(a) \]が定義域全体で成り立つことです。直感的には、グラフがつながっていれば連続、と考えればいいでしょう。
$f(x)=|x|$ は、「連続だが微分可能でない」例でしたが、この逆の「微分可能だが連続ではない」という例はありません。微分可能なら、常に連続となります。
それは、次のように示すことができます。関数 $f(x)$ が $x=a$ で微分可能であるとします。つまり、次の $f'(a)$ が存在する、ということです。\[ f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a} \]これを使って、 $x\to a$ のときに $f(x)\to f(a)$ であることを示せばいいんですね。これは
\begin{eqnarray}
\lim_{x\to a} (f(x)-f(a))
&=&
\lim_{x\to a} \frac{f(x)-f(a)}{x-a}\times (x-a) \\[5pt]
&=&
f'(a)\times 0 \\[5pt]
&=&
0
\end{eqnarray}となることから、わかります。これより、\[ \lim_{x\to a}f(x)=f(a) \]が示せました。
これは各 $x=a$ について言えるので、微分可能なら連続であることがわかります。
「微分可能なら連続」は成り立ちますが、「連続なら微分可能」は成り立ちません。つまり、微分可能であるという条件は、連続であるという条件よりも強いことがわかります。
おわりに
ここでは、微分可能でない関数の例を見た後、「連続だが微分可能でない関数があること」と「微分可能なら連続であること」を見ました。後半は抽象的な話となりましたが、「微分可能なら連続」というのは、これからもよく出てくるので理解しておきましょう。





