東京大学 理系 2019年度 第6問 解説
問題編
問題
複素数 $\alpha$, $\beta$, $\gamma$, $\delta$ および実数 a, b が、次の3条件を満たしながら動く。
条件1: $\alpha$, $\beta$, $\gamma$, $\delta$ が相異なる。
条件2: $\alpha$, $\beta$, $\gamma$, $\delta$ は4次方程式 $z^4-2z^3-2az+b=0$ の解である。
条件3:複素数 $\alpha\beta+\gamma\delta$ の実部は $0$ であり、虚部は $0$ でない。
(1) $\alpha$, $\beta$, $\gamma$, $\delta$ のうち、ちょうど2つが実数であり、残りの2つは互いに共役な複素数であることを示せ。
(2) $b$ を $a$ で表せ。
(3) 複素数 $\alpha+\beta$ がとりうる範囲を複素数平面上に図示せよ。
考え方
(1)は、4つの複素数が実数係数の4次方程式の解であることから、虚数があるとすれば、2個か4個しかありません。共役な複素数も解になることと条件3を使って示しましょう。
(2)は、条件2の方程式の係数を利用して考えていきましょう。互いに共役な複素数と実数2つであることがわかっているので、この4つの複素数は、4つの実数を使って表すことができます。これと方程式の係数から、条件を絞っていきます。
(3)は、どのように解いていけばいいのか、少しわかりづらいですが、(2)を導くときに用いた式を用いましょう。
解答編
問題
複素数 $\alpha$, $\beta$, $\gamma$, $\delta$ および実数 a, b が、次の3条件を満たしながら動く。
条件1: $\alpha$, $\beta$, $\gamma$, $\delta$ が相異なる。
条件2: $\alpha$, $\beta$, $\gamma$, $\delta$ は4次方程式 $z^4-2z^3-2az+b=0$ の解である。
条件3:複素数 $\alpha\beta+\gamma\delta$ の実部は $0$ であり、虚部は $0$ でない。
(1) $\alpha$, $\beta$, $\gamma$, $\delta$ のうち、ちょうど2つが実数であり、残りの2つは互いに共役な複素数であることを示せ。
解答
(1)
条件3より、 $\alpha$, $\beta$, $\gamma$, $\delta$ がすべて実数になることはない。なので、少なくとも1つは虚数である。
$\alpha$ を虚数としてよい。このとき、条件2から、 $\alpha$ は実数係数の4次方程式の解なので、共役複素数 $\overline{\alpha}$ もこの方程式の解となる。よって、 $\beta$, $\gamma$, $\delta$ のどれかは、 $\overline{\alpha}$ と一致する。
もし、 $\beta=\overline{\alpha}$ だとすると、 $\gamma$, $\delta$ は、ともに実数か、互いに共役複素数の関係にあるため、 $\alpha\beta+\gamma\delta$ は実数となってしまう。これは、条件3を満たさない。
よって、 $\gamma$, $\delta$ のどちらかが $\overline{\alpha}$ と一致する。 $\gamma=\overline{\alpha}$ として一般性を失わない。
ここで、もし、他の2つも虚数なら、 $\delta=\overline{\beta}$ なので、
\begin{eqnarray}
& &
\overline{ \alpha\beta+\gamma\delta } \\[5pt]
&=&
\overline{ \alpha\beta+\overline{\alpha\beta} } \\[5pt]
&=&
\overline{ \alpha\beta}+\alpha\beta \\[5pt]
&=&
\alpha\beta+\gamma\delta
\end{eqnarray}となるため、 $\alpha\beta+\gamma\delta$ は実数となり、条件3を満たさない。よって、 $\delta=\overline{\beta}$ とはならず、 $\beta$, $\gamma$ はともに実数となる。
以上から、 $\alpha$, $\beta$, $\gamma$, $\delta$ の中には、ちょうど2つ実数があり、残りの2つは互いに共役な複素数であることがわかる。
((1)終)
解答編 つづき
問題
(2) $b$ を $a$ で表せ。
解答
(2)
(1)での議論から、 $\alpha$, $\beta$ のどちらかが実数でどちらかが虚数であり、 $\gamma$, $\delta$ のどちらかが実数でどちらかが虚数であることがわかる。
よって、実数 $p,q,r,s$ を用いて、 $\alpha$ と $\beta$ は、どちらかが $p+qi$ でどちらかが $r$ であり、 $\gamma$, $\delta$ は、どちらかが $p-qi$ でどちらかが $s$ である、としてよい。ただし、 $q\ne 0$ であり、条件1より $r\ne s$ である。
\begin{eqnarray} & & \alpha\beta+\gamma\delta \\[5pt] &=& r(p+qi)+s(p-qi) \\[5pt] &=& p(r+s) +q(r-s)i \\[5pt] \end{eqnarray}であるから、条件3より、 $p(r+s)=0$ である。条件2から、$\alpha$, $\beta$, $\gamma$, $\delta$ は、 $z^4-2z^3-2az+b=0$ の解であるから、この左辺は
\begin{eqnarray}
& &
(z-p-qi)(z-p+qi)(z-r)(z-s) \\[5pt]
&=&
\{ z^2-2pz+(p^2+q^2) \}\{ z^2-(r+s)z+rs \} \\[5pt]
\end{eqnarray}と一致する。
ここで、 $z^2$ の係数を比較すると
\begin{eqnarray}
(p^2+q^2)+rs+2p(r+s) &=& 0
\end{eqnarray}が得られる。先ほど、条件3から $p(r+s)=0$ が導けていたので、これより、\[ p^2+q^2=-rs \cdots \ (*) \]が得られる。
続いて、 $z^3$ の係数を比較すると
\begin{eqnarray}
-2p-(r+s) &=& -2 \\[5pt]
\end{eqnarray}が得られる。条件3から $p(r+s)=0$ だったので、 $p=0$ とすると $r+s=2$ であり、 $r+s=0$ とすると $p=1$ であることがわかる。
定数項から
\begin{eqnarray}
rs(p^2+q^2) &=& b \\[5pt]
-r^2s^2 &=& b \\[5pt]
\end{eqnarray}が得られる。
最後に、 $z$ の係数を比較して
\begin{eqnarray}
-2prs-(p^2+q^2)(r+s) &=& -2a \\[5pt]
-2prs+rs(r+s) &=& -2a \\[5pt]
rs\{-2p+(r+s)\} &=& -2a \\[5pt]
\end{eqnarray}が得られる。 $p=0$, $r+s=2$ のときは、この式から $a=-rs$ が導かれ、 $p=1$, $r+s=0$ のときは $a=rs$ が導かれる。どちらの場合も、 $r^2s^2=a^2$ なので、\[ b=-r^2s^2=-a^2 \]となる。
((2)終)
解答編 つづき
問題
(3) 複素数 $\alpha+\beta$ がとりうる範囲を複素数平面上に図示せよ。
解答
(3)
ここまでの議論から、 $\alpha, \beta$ のどちらかは複素数で、どちらかは実数であることがわかる。以下では、(2)と同じ記号を用いる。
(i) $p=1$, $r+s=0$ のとき
(*)より、\[ 1+q^2=-r(-r)=r^2 \]が成り立つ。これを満たす $r,q$ のうち、 $q\ne 0$ となるものを1組定めると、複素数 $\alpha$, $\beta$, $\gamma$, $\delta$ と実数 $a,b$ が定まり、3つの条件を満たすことがわかる。
$\alpha+\beta=X+Yi$ とする(X, Y は実数)と、\[ 1+r=X, q=Y \]であることから
\begin{eqnarray}
1+Y^2 &=& (X-1)^2 \\[5pt]
(X-1)^2-Y^2 &=& 1 \\[5pt]
\end{eqnarray}が得られる。
(ii) $p=0$, $r+s=2$ のとき
(*)より、\[ q^2=-r(2-r)=(r-1)^2-1 \]が成り立つ。これを満たす $r,q$ のうち、 $q\ne 0$ となるものを1組定めると、複素数 $\alpha$, $\beta$, $\gamma$, $\delta$ と実数 $a,b$ が定まり、3つの条件を満たすことがわかる。
$\alpha+\beta=X+Yi$ とする(X, Y は実数)と、\[ r=X, q=Y \]であることから
\begin{eqnarray}
Y^2 &=& (X-1)^2-1 \\[5pt]
(X-1)^2-Y^2 &=& 1 \\[5pt]
\end{eqnarray}が得られる。
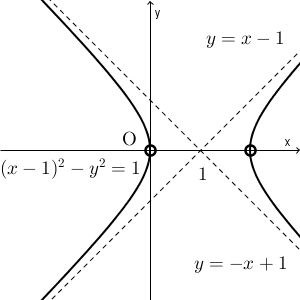
以上より、複素数 $\alpha+\beta$ がとり得る範囲は、双曲線 $(X-1)^2-Y^2 = 1$ から $Y=0$ となる点を除いた部分となる。
(終)





