東京大学 理系 2019年度 第3問 解説
問題編
問題
座標空間内に5点 $\mathrm{ A }(2,0,0)$, $\mathrm{ B }(0,2,0)$, $\mathrm{ C }(-2,0,0)$, $\mathrm{ D }(0,-2,0)$, $\mathrm{ E }(0,0,-2)$ を考える。線分 AB の中点 M と線分 AD の中点 N を通り、直線 AE に平行な平面を $\alpha$ とする。さらに、 p は $2\lt p \lt 4$ をみたす実数とし、点 $\mathrm{ P }(p,0,2)$ を考える。
(1) 八面体 PABCDE の平面 $y=0$ による切り口および、平面 $\alpha$ の平面 $y=0$ による切り口を同一平面上に図示せよ。
(2) 八面体 PABCDE の平面 $\alpha$ による切り口が八角形となる p の範囲を求めよ。
(3) 実数 p が(2)で定まる範囲にあるとする。八面体 PABCDE の平面 $\alpha$ による切り口のうち $y\geqq 0$, $z\geqq 0$ の部分を点 $(x,y,z)$ が動くとき、座標平面上で点 $(y.z)$ が動く範囲の面積を求めよ。
考え方
考えにくい問題ですが、前半は平面 $y=0$ で切ることを前提にして空間図形をかいてみるとわかりやすいかもしれません。
(1)では、「同一平面上に図示せよ」というのがポイントで、 $p$ の値によって切り口の交差の仕方が変わることに注意しましょう。(2)は、平面が八面体のすべての面を切る場合を考えます。
(3)は、どこの部分のことを言ってるのかを把握するのがまた大変ですが、よく考えると点の動く範囲は四角形になることがわかります。なので、4頂点の座標さえわかれば、面積を出すのは簡単です。頑張って座標を求めましょう。
解答編
問題
座標空間内に5点 $\mathrm{ A }(2,0,0)$, $\mathrm{ B }(0,2,0)$, $\mathrm{ C }(-2,0,0)$, $\mathrm{ D }(0,-2,0)$, $\mathrm{ E }(0,0,-2)$ を考える。線分 AB の中点 M と線分 AD の中点 N を通り、直線 AE に平行な平面を $\alpha$ とする。さらに、 p は $2\lt p \lt 4$ をみたす実数とし、点 $\mathrm{ P }(p,0,2)$ を考える。
(1) 八面体 PABCDE の平面 $y=0$ による切り口および、平面 $\alpha$ の平面 $y=0$ による切り口を同一平面上に図示せよ。
解答
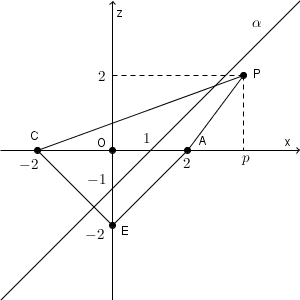
各点は次のようになる。
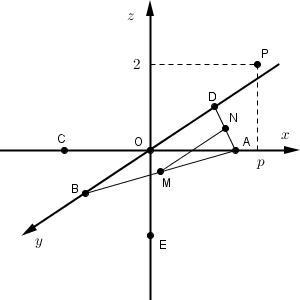
点 B, D は平面 $y=0$ 上になく、点 P, A, C, E は平面 $y=0$ 上にあるため、八面体 PABCDE を平面 $y=0$ で切った断面は次の図の青線のようになる。
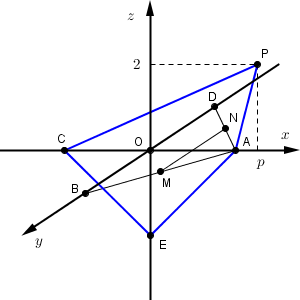
また、線分 MN は平面 $y=0$ と $(1,0,0)$ で交わり、直線 AE に平行であるから、平面 $\alpha$ を平面 $y=0$ で切ったときの断面は、直線 $z=x-1$ となる。この直線上に点 P があるとすると、\[ 2=p-1 \]なので、$p=3$ となる。 $p\lt 3$ のときは、直線 $z=x-1$ は辺 AP と交わり、 $p\gt 3$ のときは辺 CP と交わる。
以上から、切り口は次のようになる。
・$2\lt p \lt 3$ のとき
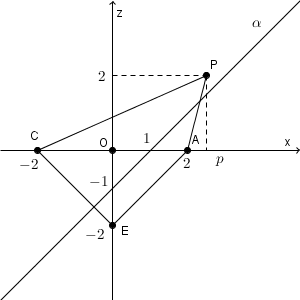
・$p=3$ のとき
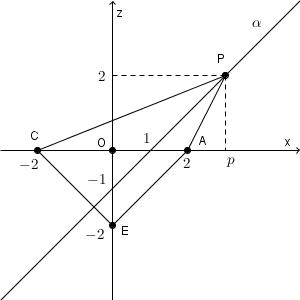
・$3\lt p \lt 4$ のとき
((1)終)
解答編 つづき
問題
(2) 八面体 PABCDE の平面 $\alpha$ による切り口が八角形となる p の範囲を求めよ。
解答
八面体を平面で切ったときの切り口が八角形となるのは、その平面が八面体のすべての面を切るときである。なので、平面 $\alpha$ が8つの面をすべて切る場合を求める。
点 B, D から平面 $y=0$ に下した垂線の足は、原点 $\mathrm{ O }(0,0,0)$ である。(1)の解より、平面 $y=0$ による平面 $\alpha$ の切り口は OE と交わっているため、平面 $\alpha$ は、辺 BE, DE を含む面を切ることがわかる。よって、平面 $\alpha$ は、頂点 E を含む4つの面を切ることがわかる。
また、平面 $y=0$ による平面 $\alpha$ の切り口は AO と交わっているため、平面 $\alpha$ は、辺 AB, AD を含む面を切ることがわかる。よって、平面 $\alpha$ は、面 APB, APD も切ることがわかる。
残りの面 BPC, DPC については、平面 $y=0$ で考えると、 $z=x-1$ が 線分 OP, CP, CO のどれかと、両端の点以外で交わっているときを考えればよい。そのような場合は、(1)の解より、 $3\lt p \lt 4$ のときであることがわかる。
よって、求める範囲は、 $3\lt p \lt 4$ である。
((2)終)
解答編 つづき
問題
(3) 実数 p が(2)で定まる範囲にあるとする。八面体 PABCDE の平面 $\alpha$ による切り口のうち $y\geqq 0$, $z\geqq 0$ の部分を点 $(x,y,z)$ が動くとき、座標平面上で点 $(y.z)$ が動く範囲の面積を求めよ。
解答
八面体 PABCDE を平面 $\alpha$ で切ったときの $y\geqq 0$, $z\geqq 0$ の部分の切り口を考えるには、この八面体の $y\geqq 0$, $z\geqq 0$ の部分だけを考えればよい。
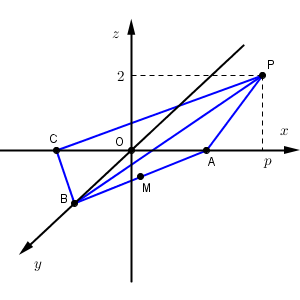
平面 $\alpha$ と、辺 AB との共有点は、点 M であり、辺 AC との共有点は、点 $(1,0,0)$ である。以下では、平面 $\alpha$ と、辺 CP, BP との共有点の座標を求める。

平面 $y=0$ での切り口で考えると、直線 CP の方程式は
\begin{eqnarray}
z &=& \frac{2}{p+2}(x+2)
\end{eqnarray}であり、平面 $\alpha$ の切り口は $z=x-1$ だから、交点の $x$ 座標は
\begin{eqnarray}
\frac{2}{p+2}(x+2) &=& x-1 \\[5pt]
2(x+2) &=& (p+2)(x-1) \\[5pt]
2x+4 &=& (p+2)x-p-2 \\[5pt]
px &=& p+6 \\[5pt]
x &=& \frac{p+6}{p} \\[5pt]
\end{eqnarray}であり、 $z$ 座標は\[ \frac{p+6}{p}-1=\frac{6}{p} \]だから、辺 PC と平面 $\alpha$ との交点は $\left(\dfrac{p+6}{p},0,\dfrac{6}{p}\right)$ となる。
次に、平面 $y=0$ での切り口で考えると、直線 OP の方程式は
\begin{eqnarray}
z &=& \frac{2}{p}x
\end{eqnarray}だから、 $z=x-1$ との交点の $x$ 座標は
\begin{eqnarray}
\frac{2}{p}x &=& x-1 \\[5pt]
2x &=& px-p \\[5pt]
(p-2)x &=& p \\[5pt]
x &=& \frac{p}{p-2} \\[5pt]
\end{eqnarray}であるから、辺 BP と平面 $\alpha$ との共有点は、辺 BP を $\dfrac{p}{p-2}:\left(p-\dfrac{p}{p-2}\right)=1:p-3$ に内分する点であることがわかる。よって
\begin{eqnarray}
& &
\left(p\cdot\frac{1}{p-2},2\cdot\frac{p-3}{p-2}, 2\cdot\frac{1}{p-2}\right) \\[5pt]
&=&
\left(\frac{p}{p-2},\frac{2p-6}{p-2}, \frac{2}{p-2}\right) \\[5pt]
\end{eqnarray}となる。
以上から、八面体 PABCDE の平面 $\alpha$ による切り口のうち、 $y\geqq 0$, $z\geqq 0$ の部分は、4点 $(1,1,0)$, $(1,0,0)$, $\left(\dfrac{p+6}{p},0,\dfrac{6}{p}\right)$, $\left(\dfrac{p}{p-2},\dfrac{2p-6}{p-2}, \dfrac{2}{p-2}\right)$ で囲まれた四角形となる。よって、この部分を点 $(x,y,z)$ が動くとき、座標平面上で点 $(y,z)$ が動く範囲は、4点 $(1,0)$, $(0,0)$, $\left(0,\dfrac{6}{p}\right)$, $\left(\dfrac{2p-6}{p-2}, \dfrac{2}{p-2}\right)$ で囲まれた四角形となる。
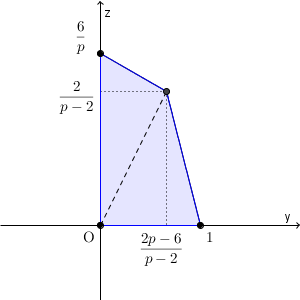
以上から、求める図形の面積は、 この四角形の面積なので
\begin{eqnarray}
& &
\frac{1}{2}\cdot\frac{6}{p}\cdot\frac{2p-6}{p-2}
+\frac{1}{2}\cdot1\cdot\frac{2}{p-2} \\[5pt]
&=&
\frac{3(2p-6)+p}{p(p-2)} \\[5pt]
&=&
\frac{7p-18}{p(p-2)} \\[5pt]
\end{eqnarray}となる。
((3)終)





