共通テスト 数学I・数学A 2022年度 第2問 [1] 解説

【必答問題】

問題編

問題

　$p, q$ を実数とする。

　花子さんと太郎さんは、次の二つの2次方程式について考えている。
\begin{eqnarray} x^2+px+q &=& 0 \quad \cdots ① \\[5pt] x^2+qx+p &=& 0 \quad \cdots ② \\[5pt] \end{eqnarray} 　①または②を満たす実数 $x$ の個数を $n$ とおく。

(1) $p=4$, $q=-4$ のとき、 $n=\myBox{ア}$ である。
　また、 $p=1$, $q=--2$ のとき、 $n=\myBox{イ}$ である。

(2) $p=-6$ のとき、 $n=3$ になる場合を考える。

• 例えば、①と②をともに満たす実数 $x$ があるときは $n=3$ になりそうだね。
• それを $\alpha$ としたら、 $\alpha^2-6\alpha+q=0$ と $\alpha^2+q\alpha-6=0$ が成り立つよ。
• なるほど。それならば $\alpha^2$ を消去すれば、 $\alpha$ の値が求められそうだね。
• 確かに $\alpha$ の値が求まるけど、実際に $n=3$ となっているかどうかの確認が必要だね。
• これ以外にも $n=3$ となる場合がありそうだね。

　$n=3$ となる $q$ の値は\[ q=\myBox{ウ},\ \myBox{エ} \]である。ただし、 $\mybox{ウ}\lt\mybox{エ}$ とする。

(3) 花子さんと太郎さんは、グラフ表示ソフトを用いて、①, ②の左辺を $y$ とおいた2次関数 $y=x^2+px+q$ と $y=x^2+qx+p$ のグラフの動きを考えている。

　$p=-6$ に固定したまま、 $q$ の値だけを変化させる。
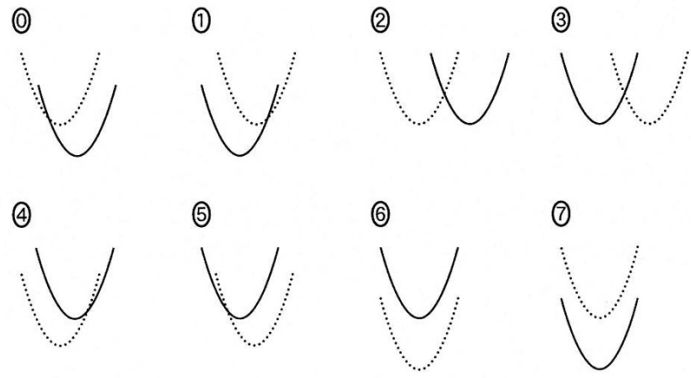
\begin{eqnarray} y&=&x^2-6x+q \quad \cdots ③ \\[5pt] y&=&x^2+qx-6 \quad \cdots ④ \\[5pt] \end{eqnarray}の二つのグラフについて、 $q=1$ のときのグラフを点線で、 $q$ の値を $1$ から増加させたときのグラフを実線でそれぞれ表す。このとき、③のグラフの移動の様子を示すと $\dBox{オ}$ となり、④のグラフの移動の様子を示すと $\dBox{カ}$ となる。

　$\dbox{オ}$, $\dbox{カ}$ については、最も適切なものを、次の 0 ～ 7のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、 $x$ 軸と $y$ 軸は省略しているが、 $x$ 軸は右方向、 $y$ 軸は上方向がそれぞれ正の方向である。

(4) $\mybox{ウ}\lt q\lt \mybox{エ}$ とする。全体集合 $U$ を実数全体の集合とし、 $U$ の部分集合 $A, B$ を
\begin{eqnarray} A &=& \{x\mid x^2-6x+q\lt 0\} \\[5pt] B &=& \{x\mid x^2+qx-6\lt 0\} \\[5pt] \end{eqnarray}とする。 $U$ の部分集合 $X$ に対し、 $X$ の補集合を $\bar{X}$ と表す。このとき、次のことが成り立つ。

　$x\in A$ は、 $x\in B$ であるために $\dBox{キ}$。
　$x\in B$ は、 $x\in \bar{A}$ であるために $\dBox{ク}$。

　$\dbox{キ}$, $\dbox{ク}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 必要条件であるが、十分条件ではない
　1: 十分条件であるが、必要条件ではない
　2: 必要十分条件である
　3: 必要条件でも十分条件でもない

考え方

2次方程式、2次関数とそのグラフ、2次不等式と、まんべんなく出題されています。テーマがころころ変わるので、頑張ってついていきましょう。

(3)のグラフを移動する問題は、頂点に着目するといいでしょう。(4)は今までの話を利用すれば、グラフの位置関係がわかりますが、少し難しいかもしれません。

【必答問題】

解答編

問題

　$p, q$ を実数とする。

　花子さんと太郎さんは、次の二つの2次方程式について考えている。
\begin{eqnarray} x^2+px+q &=& 0 \quad \cdots ① \\[5pt] x^2+qx+p &=& 0 \quad \cdots ② \\[5pt] \end{eqnarray} 　①または②を満たす実数 $x$ の個数を $n$ とおく。

(1) $p=4$, $q=-4$ のとき、 $n=\myBox{ア}$ である。
　また、 $p=1$, $q=--2$ のとき、 $n=\myBox{イ}$ である。

解説

$x^2+4x-4=0$ の解は $x=-2\pm2\sqrt{2}$ であり、 $x^2-4x+4=0$ の解は $x=2$ なので、 $p=4, q=-4$ のときは $n=3$ です。

また、 $x^2+x-2=0$ は $(x+2)(x-1)=0$ と変形できるので、解は $x=1,-2$ です。また、 $x^2-2x+1=0$ の解は $x=1$ です。 $x=1$ がダブっているので、 $p=1,q=-2$ のときは $n=2$ です。

解答

ア：3
イ：2

解答編 つづき

(2) $p=-6$ のとき、 $n=3$ になる場合を考える。

• 例えば、①と②をともに満たす実数 $x$ があるときは $n=3$ になりそうだね。
• それを $\alpha$ としたら、 $\alpha^2-6\alpha+q=0$ と $\alpha^2+q\alpha-6=0$ が成り立つよ。
• なるほど。それならば $\alpha^2$ を消去すれば、 $\alpha$ の値が求められそうだね。
• 確かに $\alpha$ の値が求まるけど、実際に $n=3$ となっているかどうかの確認が必要だね。
• これ以外にも $n=3$ となる場合がありそうだね。

　$n=3$ となる $q$ の値は\[ q=\myBox{ウ},\ \myBox{エ} \]である。ただし、 $\mybox{ウ}\lt\mybox{エ}$ とする。

解説

2次方程式の解は2個以下なので、 $n=3$ となるのは、以下のようなケースがあります。

「どちらの2次方程式も異なる解を2つ持ち、そのうちの解の1つが重複している（会話で言及されているケース）」
「どちらかの2次方程式の解が1個（重解）で、他方の2次方程式の解が2個であり、これら3つがすべて異なる」

前者のケースでは、会話で言及されている通り、 $\alpha$ を含んだ2つの式から $\alpha^2$ を消去すれば
\begin{eqnarray} (-6-q)\alpha+q+6 &=& 0 \end{eqnarray}となります。もし $q=-6$ なら、2つの方程式は同じになってしまい、 $n=3$ にはなりません。 $q\ne -6$ のときは $\alpha=1$ となります。

$\alpha=1$ とすると $\alpha^2-6\alpha+q=0$ から $q=5$ が得られます。この場合に、 $n=3$ となるか確かめてみます（他の解が重複していたり、2次方程式が重解となっているケースがありえるので）。

$x^2-6x+5=0$ は $(x-1)(x-5)=0$ なので、解は $x=1,5$ です。また、 $x^2+5x-6=0$ は $(x-1)(x+6)=0$ なので、解は $x=1,-6$ です。なので、①または②を満たす実数 $x$ は $1,5,-6$ の3個なので、たしかに $n=3$ となります。

次に、片方の2次方程式が重解を持ち、もう片方が異なる2つの実数解を持つケースを考えてみましょう。

$x^2-6x+q=0$ が重解を持つとすると、 $q=9$ で、解は $x=3$ となります。このとき、 $x^2+9x-6=0$ は判別式が正です。また、 $x=3$ は解でありません。なので、 $n=3$ だとわかります。

なお、 $x^2+qx-6=0$ の判別式は必ず正になるので、これが重解を持つことはありません。

以上から、 $n=3$ となる $q$ の値は、 $q=5, 9$ となります。

解答

ウ：5
エ：9

解答編 つづき

(3) 花子さんと太郎さんは、グラフ表示ソフトを用いて、①, ②の左辺を $y$ とおいた2次関数 $y=x^2+px+q$ と $y=x^2+qx+p$ のグラフの動きを考えている。

　$p=-6$ に固定したまま、 $q$ の値だけを変化させる。
\begin{eqnarray} y&=&x^2-6x+q \quad \cdots ③ \\[5pt] y&=&x^2+qx-6 \quad \cdots ④ \\[5pt] \end{eqnarray}の二つのグラフについて、 $q=1$ のときのグラフを点線で、 $q$ の値を $1$ から増加させたときのグラフを実線でそれぞれ表す。このとき、③のグラフの移動の様子を示すと $\dBox{オ}$ となり、④のグラフの移動の様子を示すと $\dBox{カ}$ となる。

　$\dbox{オ}$, $\dbox{カ}$ については、最も適切なものを、次の 0 ～ 7のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、 $x$ 軸と $y$ 軸は省略しているが、 $x$ 軸は右方向、 $y$ 軸は上方向がそれぞれ正の方向である。

解説

$y=x^2-6x+q$ のグラフで $q=1$ のときからどんどん増やしていくと、グラフは真上にスライドしていきます。なので、選択肢では 6 となります。

また
\begin{eqnarray} y &=& x^2+qx-6 \\[5pt] &=& \left(x+\dfrac{q}{2}\right)^2-\dfrac{q^2}{4}-6 \\[5pt] \end{eqnarray}となるので、頂点は $\left(-\dfrac{q}{2}, -\dfrac{q^2}{4}-6\right)$ となります。 $q$ を $1$ からどんどん増やしていくと、頂点の $x$ 座標も $y$ 座標も減少していきます。そのため、実線のグラフの頂点が点線のグラフの頂点の左下にあるようなものが答えとなります。選択肢では 1 となります。

解答

オ：6
カ：1

解答編 つづき

(4) $\mybox{ウ}\lt q\lt \mybox{エ}$ とする。全体集合 $U$ を実数全体の集合とし、 $U$ の部分集合 $A, B$ を
\begin{eqnarray} A &=& \{x\mid x^2-6x+q\lt 0\} \\[5pt] B &=& \{x\mid x^2+qx-6\lt 0\} \\[5pt] \end{eqnarray}とする。 $U$ の部分集合 $X$ に対し、 $X$ の補集合を $\bar{X}$ と表す。このとき、次のことが成り立つ。

　$x\in A$ は、 $x\in B$ であるために $\myBox{キ}$。
　$x\in B$ は、 $x\in \bar{A}$ であるために $\myBox{ク}$。

　$\mybox{キ}$, $\mybox{ク}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 必要条件であるが、十分条件ではない
　1: 十分条件であるが、必要条件ではない
　2: 必要十分条件である
　3: 必要条件でも十分条件でもない

解説

グラフを使って考えてみます。

まずは $q=5$ のときを考えてみます。(1)で見たように、 $y=x^2-6x+5$ と $y=x^2+5x-6$ は $x=1$ を共通の解として持っていて、グラフは次のようになります。なお、右が $y=x^2-6x+5$ のグラフです。

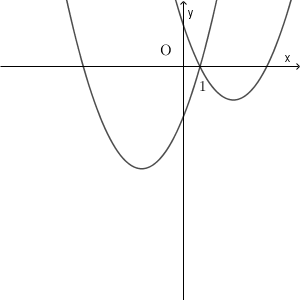
$q$ の値を大きくしていくと、(3)で見たように、 $y=x^2-6x+q$ のグラフは真上に移動し、 $y=x^2+qx-6$ のグラフは左下に移動していきます。 $q=9$ のときには次のようになります。 $x$ 軸との共有点は全部で3つになります。

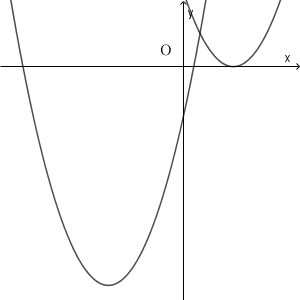
この間では、次のような位置関係になっています。

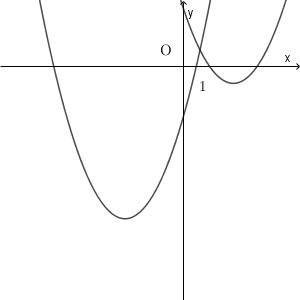
ここで、 $x=1$ とすると、どちらの $y$ 座標も $q-5$ となり、必ず正になることがわかります。このことと、 $y=x^2-6x+q$ のグラフは真上に、$y=x^2+qx-6$ のグラフは左下に移動することから、2つの集合 $A$ と $B$ には、共通部分はないことがわかります。

このことから、 $x\in A$ は $x\in B$ の必要条件でも十分条件でもないことがわかります。

また、 $x\in B$ ならば、必ず $x^2-6x+q\geqq 0$ なので $x\in \bar{A}$ だとわかります。一方、 $x=1$ を考えると、 $x\in\bar{A}$ であっても $x\in B$ とは限りません。以上より、 $x\in B$ は $x\in\bar{A}$ の十分条件ではあるが必要条件ではないことがわかります。

解答

キ：3
ク：1