共通テスト 数学I・数学A 2022年度 第1問 [2] 解説
【必答問題】
(三角比の表は省略しています)
問題編
問題
以下の問題を解答するにあたっては、必要に応じて41ページの三角比の表を用いてもよい。
太郎さんと花子さんは、キャンプ場のガイドブックにある地図を見ながら、後のように話している。
- キャンプ場の地点 A から山頂 B を見上げる角度はどれくらいかな。
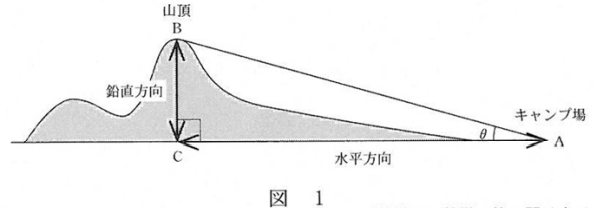
- 地図アプリを使って、地点 A と山頂 B を含む断面図を調べたら、図1のようになったよ。点 C は山頂 B から地点 A を通る水平面に下した垂線とその水平面との交点のことだよ。
- 図1の角度 $\theta$ は、 AC、BC の長さを定規で測って、三角比の表を用いて調べたら $16^{\circ}$ だったよ。
- 本当に $16^{\circ}$ なの? 図1の鉛直方向の縮尺と水平方向の縮尺は等しいのかな?
図1の $\theta$ はちょうど $16^{\circ}$ であったとする。しかし、図1の縮尺は、水平方向が $\dfrac{1}{100000}$ であるのに対して、鉛直方向は $\dfrac{1}{25000}$ であった。
実際にキャンプ場の地点 A から山頂を見上げる角である $\angle \mathrm{ BAC }$ を考えると、 $\tan\angle \mathrm{ BAC }$ は $\myBox{コ}.\myBox{サシス}$ となる。したがって、 $\angle \mathrm{ BAC }$ の大きさは $\dBox{セ}$ 。ただし、目の高さは無視して考えるものとする。
$\dbox{セ}$ の解答群
0: $3^{\circ}$ より大きく $4^{\circ}$ より小さい
1: ちょうど $4^{\circ}$ である
2: $4^{\circ}$ より大きく $5^{\circ}$ より小さい
3: ちょうど $16^{\circ}$ である
4: $48^{\circ}$ より大きく $49^{\circ}$ より小さい
5: ちょうど $49^{\circ}$ である
6: $49^{\circ}$ より大きく $50^{\circ}$ より小さい
7: $63^{\circ}$ より大きく $64^{\circ}$ より小さい
8: ちょうど $64^{\circ}$ である
9: $64^{\circ}$ より大きく $65^{\circ}$ より小さい
考え方
鉛直方向と水平方向の長さを変換して考えます。何か1つの長さを基準にして、登場するいろんな長さを表すようにすると計算しやすいでしょう。
【必答問題】
解答編
問題
以下の問題を解答するにあたっては、必要に応じて41ページの三角比の表を用いてもよい。
太郎さんと花子さんは、キャンプ場のガイドブックにある地図を見ながら、後のように話している。
- キャンプ場の地点 A から山頂 B を見上げる角度はどれくらいかな。
- 地図アプリを使って、地点 A と山頂 B を含む断面図を調べたら、図1のようになったよ。点 C は山頂 B から地点 A を通る水平面に下した垂線とその水平面との交点のことだよ。
- 図1の角度 $\theta$ は、 AC、BC の長さを定規で測って、三角比の表を用いて調べたら $16^{\circ}$ だったよ。
- 本当に $16^{\circ}$ なの? 図1の鉛直方向の縮尺と水平方向の縮尺は等しいのかな?
図1の $\theta$ はちょうど $16^{\circ}$ であったとする。しかし、図1の縮尺は、水平方向が $\dfrac{1}{100000}$ であるのに対して、鉛直方向は $\dfrac{1}{25000}$ であった。
実際にキャンプ場の地点 A から山頂を見上げる角である $\angle \mathrm{ BAC }$ を考えると、 $\tan\angle \mathrm{ BAC }$ は $\myBox{コ}.\myBox{サシス}$ となる。したがって、 $\angle \mathrm{ BAC }$ の大きさは $\dBox{セ}$ 。ただし、目の高さは無視して考えるものとする。
$\dbox{セ}$ の解答群
0: $3^{\circ}$ より大きく $4^{\circ}$ より小さい
1: ちょうど $4^{\circ}$ である
2: $4^{\circ}$ より大きく $5^{\circ}$ より小さい
3: ちょうど $16^{\circ}$ である
4: $48^{\circ}$ より大きく $49^{\circ}$ より小さい
5: ちょうど $49^{\circ}$ である
6: $49^{\circ}$ より大きく $50^{\circ}$ より小さい
7: $63^{\circ}$ より大きく $64^{\circ}$ より小さい
8: ちょうど $64^{\circ}$ である
9: $64^{\circ}$ より大きく $65^{\circ}$ より小さい
解説
図1上で $\mathrm{ AC }=x$ とすると、 $\mathrm{ BC }=x\tan 16^{\circ}$ となります。
実際の距離は、縮尺を考えて $\mathrm{AC}$ が $100000x$ であり、 $\mathrm{BC}=25000x\tan 16^{\circ}$ となります。なので、実際の角で考えると $\tan16^{\circ}=0.2867$ であることも用いて
\begin{eqnarray}
\tan\angle \mathrm{ BAC }
&=&
\frac{25000x\tan 16^{\circ} }{100000x} \\[5pt]
&=&
\frac{\tan 16^{\circ} }{4} \\[5pt]
&=&
\frac{0.2867}{4} \\[5pt]
&=&
0.071675 \\[5pt]
\end{eqnarray}となります。小数第4位を四捨五入すると $0.072$ となります。
三角比の表を見ると、 $\tan4^{\circ}=0.0699$ と $\tan5^{\circ}=0.0875$ から、 $\angle \mathrm{ BAC }$ は $4^{\circ}$ より大きく、 $5^{\circ}$ より小さいことがわかります。
解答
コサシス:0072
セ:2