共通テスト 数学I・数学A 2022年度 第5問 解説

【第3問～第5問から2問選択】

問題編

問題

　$\triangle \mathrm{ABC}$ の重心を G とし、線分 AG 上で点 A とは異なる位置に点 D をとる。直線 AG と辺 BC の交点を E とする。また、直線 BC 上で辺 BC 上にはない位置に点 F をとる。直線 DF と辺 AB の交点を P、直線 DF と辺 AC の交点を Q とする。

(1) 点 D は線分 AG の中点であるとする。このとき、 $\triangle \mathrm{ABC}$ の形状に関係なく\[ \frac{\mathrm{AD} }{\mathrm{DE} }=\frac{\myBox{ア} }{\myBox{イ} } \]である。また、点 F の位置に関係なく
\begin{eqnarray} \frac{\mathrm{BP} }{\mathrm{AP} } &=& \myBox{ウ}\times\frac{\dBox{エ} }{\dBox{オ} }, \\[5pt] \frac{\mathrm{CQ} }{\mathrm{AQ} } &=& \myBox{カ}\times\frac{\dBox{キ} }{\dBox{ク} } \\[5pt] \end{eqnarray}であるので、つねに\[ \frac{\mathrm{BP} }{\mathrm{AP} } + \frac{\mathrm{CQ} }{\mathrm{AQ} }=\myBox{ケ} \]となる。

　$\dbox{エ}$, $\dbox{オ}$, $\dbox{キ}$, $\dbox{ク}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\mathrm{BC}$
　1: $\mathrm{BF}$
　2: $\mathrm{CF}$
　3: $\mathrm{EF}$
　4: $\mathrm{FP}$
　5: $\mathrm{FQ}$
　6: $\mathrm{PQ}$

(2) $\mathrm{AB}=9$, $\mathrm{BC}=8$, $\mathrm{AC}=6$ とし、(1)と同様に、点 D は線分 AG の中点であるとする。ここで、4点 B, C, Q, P が同一円周上にあるように点 F をとる。

　このとき、 $\mathrm{AQ}=\dfrac{\myBox{コ} }{\myBox{サ} }\mathrm{AP}$ であるから\[ \mathrm{AP}=\frac{\myBox{シス} }{\myBox{セ} },\ \mathrm{AQ}=\frac{\myBox{ソタ} }{\myBox{チ} } \]であり\[ \mathrm{CF}=\frac{\myBox{ツテ} }{\myBox{トナ} } \]である。

(3) $\triangle \mathrm{ABC}$ の形状や点 F の位置に関係なく、つねに $\dfrac{\mathrm{BP} }{\mathrm{AP} }+\dfrac{\mathrm{CQ} }{\mathrm{AQ} }=10$ となるのは、 $\dfrac{\mathrm{AD} }{\mathrm{DG} }=\dfrac{\myBox{ニ} }{\myBox{ヌ} }$ のときである。

考え方

抽象的な設定が多くて考えづらいです。「形状に関係なく」とか「点の位置に関係なく」というワードのせいで難しく感じるかもしれませんが、そもそも「〇〇の定理」というのは一般的なケースで成り立つものなので、これは「何かの定理を使って考えなさい」と言ってるだけです。

最後の(3)は(1)を見ながら考えるとわかりやすいでしょう。

解答編

問題

　$\triangle \mathrm{ABC}$ の重心を G とし、線分 AG 上で点 A とは異なる位置に点 D をとる。直線 AG と辺 BC の交点を E とする。また、直線 BC 上で辺 BC 上にはない位置に点 F をとる。直線 DF と辺 AB の交点を P、直線 DF と辺 AC の交点を Q とする。

(1) 点 D は線分 AG の中点であるとする。このとき、 $\triangle \mathrm{ABC}$ の形状に関係なく\[ \frac{\mathrm{AD} }{\mathrm{DE} }=\frac{\myBox{ア} }{\myBox{イ} } \]である。

解説

図は次のような感じになっています。一例です。

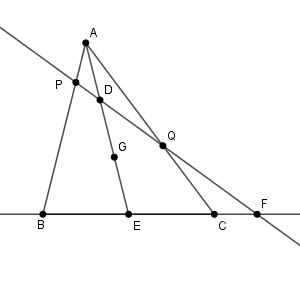
点 G は重心なので、 $\mathrm{AG}:\mathrm{GE}=2:1$ です。 D は 線分 AG の中点なので、 $\mathrm{AD}:\mathrm{DG}:\mathrm{GE}=1:1:1$ となります。よって、 $\mathrm{AD}:\mathrm{DE}=1:2$ なので、\[ \frac{\mathrm{AD} }{\mathrm{DE} }=\frac{1}{2} \]となります。

解答

アイ：12

解答編 つづき

また、点 F の位置に関係なく
\begin{eqnarray} \frac{\mathrm{BP} }{\mathrm{AP} } &=& \myBox{ウ}\times\frac{\dBox{エ} }{\dBox{オ} }, \\[5pt] \frac{\mathrm{CQ} }{\mathrm{AQ} } &=& \myBox{カ}\times\frac{\dBox{キ} }{\dBox{ク} } \\[5pt] \end{eqnarray}であるので、つねに\[ \frac{\mathrm{BP} }{\mathrm{AP} } + \frac{\mathrm{CQ} }{\mathrm{AQ} }=\myBox{ケ} \]となる。

　$\dbox{エ}$, $\dbox{オ}$, $\dbox{キ}$, $\dbox{ク}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\mathrm{BC}$
　1: $\mathrm{BF}$
　2: $\mathrm{CF}$
　3: $\mathrm{EF}$
　4: $\mathrm{FP}$
　5: $\mathrm{FQ}$
　6: $\mathrm{PQ}$

解説

AP, BP の比を考えるので、メネラウスの定理が使えそうだとわかります。三角形 ABE と直線 FP で考えると
\begin{eqnarray} \frac{\mathrm{ BP } }{\mathrm{ PA } } \cdot \frac{\mathrm{ AD } }{\mathrm{ DE } } \cdot \frac{\mathrm{ EF } }{\mathrm{ FB } } &=& 1 \\[5pt] \frac{\mathrm{ BP } }{\mathrm{ AP } } \cdot \frac{1}{2} \cdot \frac{\mathrm{ EF } }{\mathrm{ BF } } &=& 1 \\[5pt] \frac{\mathrm{ BP } }{\mathrm{ AP } } &=& 2 \times \frac{\mathrm{ BF } }{\mathrm{ EF } } \\[5pt] \end{eqnarray}となることがわかります。

また、AQ, CQ の比も、メネラウスの定理を使って求められます。三角形 ACE と直線 FP で考えると
\begin{eqnarray} \frac{\mathrm{ CQ } }{\mathrm{ QA } } \cdot \frac{\mathrm{ AD } }{\mathrm{ DE } } \cdot \frac{\mathrm{ EF } }{\mathrm{ FC } } &=& 1 \\[5pt] \frac{\mathrm{ CQ } }{\mathrm{ AQ } } \cdot \frac{1}{2} \cdot \frac{\mathrm{ EF } }{\mathrm{ CF } } &=& 1 \\[5pt] \frac{\mathrm{ CQ } }{\mathrm{ AQ } } &=& 2 \times \frac{\mathrm{ CF } }{\mathrm{ EF } } \\[5pt] \end{eqnarray}となることがわかります。

以上から、\[ \frac{\mathrm{BP} }{\mathrm{AP} } + \frac{\mathrm{CQ} }{\mathrm{AQ} } = 2\times \frac{ \mathrm{ BF } + \mathrm{ CF } }{ \mathrm{ EF } } \]となります。

ここで、点 G は重心なので、E は辺 BC の中点です。よって、 $\mathrm{ BE }=\mathrm{ CE }=x$, $\mathrm{ CF }=y$ とすると
\begin{eqnarray} 2\times \frac{ \mathrm{ BF } + \mathrm{ CF } }{ \mathrm{ EF } } = 2\times \frac{ (2x+y) + y }{ x+y }=4 \end{eqnarray}となります。

なお、上の図では、 E から見て F と C が同じ側にありますが、もし B と同じ側であれば、 $\mathrm{ BF }=y$ とおいて、
\begin{eqnarray} 2\times \frac{ \mathrm{ BF } + \mathrm{ CF } }{ \mathrm{ EF } } = 2\times \frac{ y + (2x+y) }{ x+y }=4 \end{eqnarray}となります。

いずれにしても、 $4$ という値になります。

解答

ウエオ：213
カキク：223
ケ：4

解答編 つづき

(2) $\mathrm{AB}=9$, $\mathrm{BC}=8$, $\mathrm{AC}=6$ とし、(1)と同様に、点 D は線分 AG の中点であるとする。ここで、4点 B, C, Q, P が同一円周上にあるように点 F をとる。

　このとき、 $\mathrm{AQ}=\dfrac{\myBox{コ} }{\myBox{サ} }\mathrm{AP}$ であるから\[ \mathrm{AP}=\frac{\myBox{シス} }{\myBox{セ} },\ \mathrm{AQ}=\frac{\myBox{ソタ} }{\myBox{チ} } \]であり\[ \mathrm{CF}=\frac{\myBox{ツテ} }{\myBox{トナ} } \]である。

解説

図は次のようになっています。

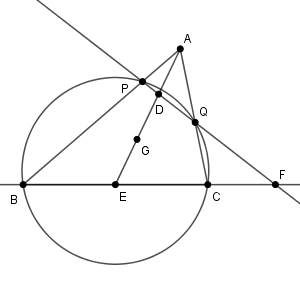
4点 B, C, Q, P が同一円周上にあることから、方べきの定理より
\begin{eqnarray} \mathrm{ AP } \cdot \mathrm{ AB } &=& \mathrm{ AQ } \cdot \mathrm{ AC } \\[5pt] 9\mathrm{ AP } &=& 6\mathrm{ AQ } \\[5pt] \mathrm{ AQ } &=& \frac{3}{2} \mathrm{ AP } \end{eqnarray}となります。

ここで、 $\mathrm{AP}=p$ とおくと、 $\mathrm{BP}=9-p$ であり、 $\mathrm{AQ}=\dfrac{3}{2}p$ と $\mathrm{CQ}=6-\dfrac{3}{2}p$ から、(1)の最後に求めた式より
\begin{eqnarray} \frac{9-p}{p}+\frac{6-\frac{3}{2}p}{\frac{3}{2}p} &=& 4 \\[5pt] 9-p +\frac{6-\frac{3}{2}p}{\frac{3}{2} } &=& 4p \\[5pt] 9-p +4-p &=& 4p \\[5pt] 6p &=& 13 \\[5pt] p &=& \frac{13}{6} \end{eqnarray}と求められます。これより、 $\mathrm{AQ}=\dfrac{3}{2}p=\dfrac{13}{4}$ もわかります。

次に、CF を求めます。上の図を見れば F は E から見て C と同じ側にあることがわかりますが、試験中はこれほど正確な図はかけないので、計算で確認しておくことにしましょう。

\[ \dfrac{\mathrm{ BP } }{\mathrm{ AP } } = \frac{9-\frac{13}{6} }{\frac{13}{6} }=\frac{41}{13} \]なので、P は辺 AB の中点より A に近いことがわかります。また、\[ \dfrac{\mathrm{ CQ } }{\mathrm{ AQ } } = \frac{6-\frac{13}{4} }{\frac{13}{4} }=\frac{11}{13} \]なので、Q は辺 AC の中点より C に近いことがわかります。こうして、F は E から見て C と同じ側にあることがわかります。

(1)で求めたように\[ \frac{\mathrm{ CQ } }{\mathrm{ AQ } } = 2 \times \frac{\mathrm{ CF } }{\mathrm{ EF } } \]が成り立ちます。ここで、左辺は先ほど求めたように $\dfrac{11}{13}$ なので
\begin{eqnarray} 2 \times \frac{\mathrm{ CF } }{\mathrm{ EF } } &=& \frac{11}{13} \\[5pt] \frac{\mathrm{ CF } }{4+\mathrm{ CF } } &=& \frac{11}{26} \\[5pt] 26\mathrm{ CF } &=& 11(4+\mathrm{ CF }) \\[5pt] 15\mathrm{ CF } &=& 44 \\[5pt] \mathrm{ CF } &=& \frac{44}{15} \\[5pt] \end{eqnarray}となります。

解答

コサ：32
シスセ：136
ソタチ：134
ツテトナ：4415

解答編 つづき

(3) $\triangle \mathrm{ABC}$ の形状や点 F の位置に関係なく、つねに $\dfrac{\mathrm{BP} }{\mathrm{AP} }+\dfrac{\mathrm{CQ} }{\mathrm{AQ} }=10$ となるのは、 $\dfrac{\mathrm{AD} }{\mathrm{DG} }=\dfrac{\myBox{ニ} }{\myBox{ヌ} }$ のときである。

解説

(1)でやった計算をよく見てみましょう。 $\mathrm{ AD }:\mathrm{ DE }=1:t$ とすると、\[ \frac{\mathrm{ BP } }{\mathrm{ AP } } = t \times \frac{\mathrm{ BF } }{\mathrm{ EF } } \]が成り立つことがわかり、\[ \frac{\mathrm{ CQ } }{\mathrm{ AQ } } = t \times \frac{\mathrm{ CF } }{\mathrm{ EF } } \]が成り立つこともわかります。これらを辺々足すと、(1)と同じように計算すれば\[ \dfrac{\mathrm{BP} }{\mathrm{AP} }+\dfrac{\mathrm{CQ} }{\mathrm{AQ} }=2t \]となるので、左辺が $10$ となるのは $t=5$ のとき、つまり、 $\mathrm{ AD }:\mathrm{ DE }=1:5$ のときだとわかります。 $\mathrm{ AE }:\mathrm{ GE }=6:2$ なので、 $\mathrm{ AD }:\mathrm{ DG }=1:3$ と求められます。こうして、 $\dfrac{\mathrm{AD} }{\mathrm{DG} }=\dfrac{1}{3}$ とわかります。

解答

ニヌ：13