共通テスト 数学I・数学A 2022年度 第2問 [2] 解説
【必答問題】
問題編
問題
日本国外における日本語教育の状況を調べるために、独立行政法人国際交流基金では「海外日本語教育機関調査」を実施しており、各国における教育機関数、教員数、学習者数が調べられている。2018年度において学習者が5000人以上の国と地域(以下、国)は29か国であった。これら29か国について、2009年度と2018年度のデータが得られている。
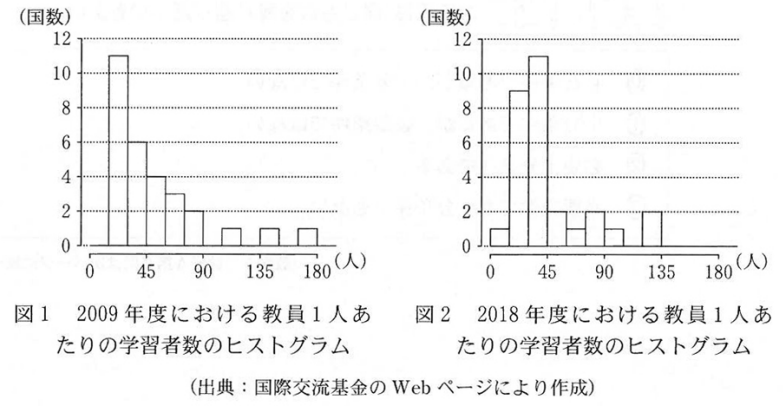
(1) 各国において、学習者数を教員数で割ることにより、国ごとの「教員1人当たりの学習者数」を算出することができる。図1と図2は、2009年度および2018年度における「教員1人あたりの学習者数」のヒストグラムである。これら二つのヒストグラムから、9年間の変化に関して、後のことが読み取れる。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
・2009年度と2018年度の中央値が含まれる階級の階級値を比較すると、 $\dBox{ケ}$ 。
・2009年度と2018年度の第1四分位数が含まれる階級の階級値を比較すると、 $\dBox{コ}$ 。
・2009年度と2018年度の第3四分位数が含まれる階級の階級値を比較すると、 $\dBox{サ}$ 。
・2009年度と2018年度の範囲を比較すると、 $\dBox{シ}$ 。
・2009年度と2018年度の四分位範囲を比較すると、 $\dBox{ス}$ 。
$\dbox{ケ}$ ~ $\dbox{ス}$ の解答群(同じものを繰り返し選んでもよい。)
0: 2018年度の方が小さい
1: 2018年度の方が大きい
2: 両者は等しい
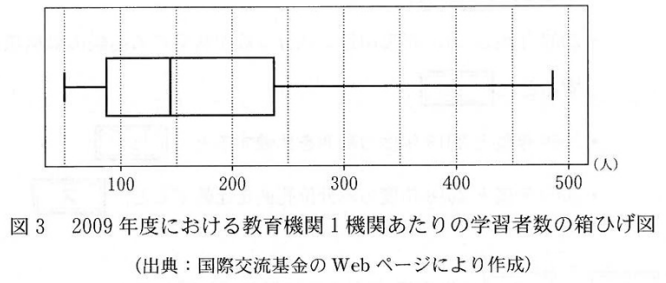
3: これら二つのヒストグラムからだけでは両者の大小を判断できない(2) 各国において、学習者数を教育機関数で割ることにより、「教育機関1機関当たりの学習者数」も算出した。図3は、2009年度における「教育機関1機関あたりの学習者数」の箱ひげ図である。
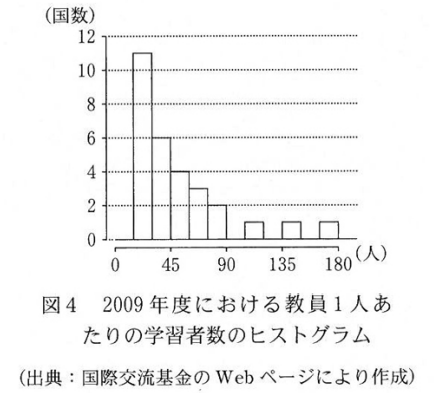
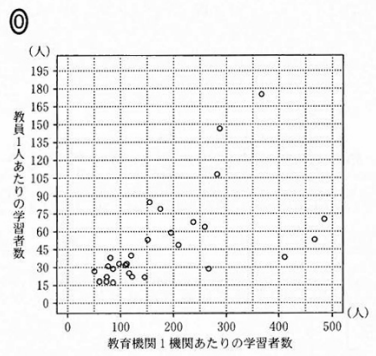
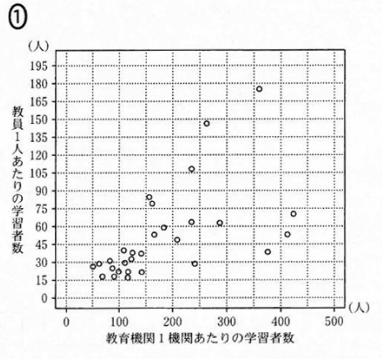
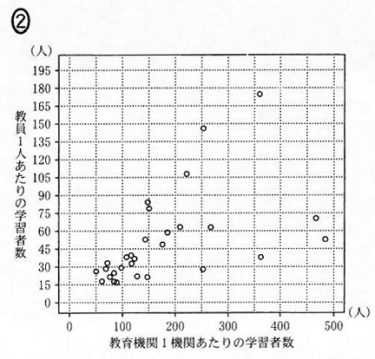
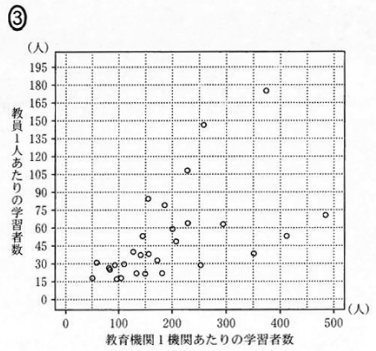
2009年度について、「教育機関1機関当たりの学習者数」(横軸)と「教員1人あたりの学習者数」(縦軸)の残布図は $\dBox{セ}$ であり。ここで、2009年度における「教員1人あたりの学習者数」のヒストグラムである(1)の図1を、図4として再掲しておく。
$\dbox{セ}$ については、最も適当なものを、次の 0 ~ 3 のうちから一つ選べ。なお、これらの散布図には、完全に重なっている点はない。
(3) 各国における2018年度の学習者数を $100$ としたときの2009年度の学習者数 $S$ 、および、各国における2018年度の教員数を $100$ としたときの2009年度の教員数 $T$ を算出した。
例えば、学習者数について説明すると、ある国において、2009年度が $44272$ 人、2018年度が $174521$ 人であった場合、2009年度の学習者数 $S$ は $\dfrac{44272}{174521}\times 100$ より $25.4$ と算出される。
表1は $S$ と $T$ について、平均値、標準偏差および共分散を計算したものである。ただし、 $S$ と $T$ の共分散は、 $S$ の偏差と $T$ の偏差の積の平均値である。
表1の数値が四捨五入していない正確な値であるとして、 $S$ と $T$ の相関係数を求めると $\myBox{ソ}. \myBox{タチ}$ である。
表1 平均値、標準偏差および共分散 $S$ の
平均値$T$ の
平均値$S$ の
標準偏差$T$ の
標準偏差$S$ と $T$ の
共分散$81.8$ $72.9$ $39.3$ $29.9$ $735.3$ (4) 表1と(3)で求めた相関係数を参考にすると、(3)で算出した2009年度の $S$ (横軸)と $T$ (縦軸)の散布図は $\dBox{ツ}$ である。
$\dbox{ツ}$ については、最も適当なものを、次の 0 ~ 3 のうちから一つ選べ。なお、これらの散布図には、完全に重なっている点はない。
考え方
どの問題も面倒です。(1)で一個一個吟味するのも大変ですし、(2)も大変です。(3)は計算が大変で、(4)は選びづらいです。かなり時間と手間のかかるセットになっています。
【必答問題】
解答編
問題
日本国外における日本語教育の状況を調べるために、独立行政法人国際交流基金では「海外日本語教育機関調査」を実施しており、各国における教育機関数、教員数、学習者数が調べられている。2018年度において学習者が5000人以上の国と地域(以下、国)は29か国であった。これら29か国について、2009年度と2018年度のデータが得られている。
(1) 各国において、学習者数を教員数で割ることにより、国ごとの「教員1人当たりの学習者数」を算出することができる。図1と図2は、2009年度および2018年度における「教員1人あたりの学習者数」のヒストグラムである。これら二つのヒストグラムから、9年間の変化に関して、後のことが読み取れる。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
・2009年度と2018年度の中央値が含まれる階級の階級値を比較すると、 $\dBox{ケ}$ 。
・2009年度と2018年度の第1四分位数が含まれる階級の階級値を比較すると、 $\dBox{コ}$ 。
・2009年度と2018年度の第3四分位数が含まれる階級の階級値を比較すると、 $\dBox{サ}$ 。
・2009年度と2018年度の範囲を比較すると、 $\dBox{シ}$ 。
・2009年度と2018年度の四分位範囲を比較すると、 $\dBox{ス}$ 。
$\dbox{ケ}$ ~ $\dbox{ス}$ の解答群(同じものを繰り返し選んでもよい。)
0: 2018年度の方が小さい
1: 2018年度の方が大きい
2: 両者は等しい
3: これら二つのヒストグラムからだけでは両者の大小を判断できない
解説
まずは、四分位数や中央値は下から何番目のデータか、を確認しておきましょう。データの数が29個なので、中央値は下から15番目です。また、第1四分位数は下位14個の中央値なので、下から7番目と8番目の平均であり、第3四分位数は、上から7番目と8番目の平均だとわかります。
これを踏まえると、まず、中央値は、2009年度は「30以上45未満」の階級に含まれ、2018年度も「30以上45未満」の階級に含まれることがわかります。階級値とは、その階級の中央の値のことなので、同じ階級値となります、選択肢2が答えです。
第1四分位数は、2009年度は「15以上30未満」の階級に、2018年度も「15以上30未満」の階級に含まれるので、これも同じ階級値となります。選択肢2が答えです。
第3四分位数は、2009年度は「60以上75未満」の階級に含まれます。2018年度は、「45以上60未満」の階級に含まれます。なので、2018年度の方が小さいので、選択肢0が答えです。
次に範囲を考えます。2009年度のほうは、最小値は大きくても30で、最大値は小さくても165なので、少なくとも135以上です。一方、2018年度のほうは範囲が135未満だとわかるので、範囲は2018年度の方が小さいことがわかります。選択肢0が答えです。
最後に四分位範囲を考えます。第1四分位数と第3四分位数が含まれる階級から考えると、2009年度の四分位範囲は30より大きく60より小さいことがわかります。2018年度は、15より大きく45より小さいことがわかります。このことから、大小は決まらないことがわかります。
例えば、2009年度の「15以上30未満」の階級に属する値がすべて25で、「60以上75未満」に属する値がすべて60だったとしましょう。このとき、2009年度の四分位範囲は35です。
もし2018年度の「15以上30未満」の階級に属する値がすべて15で、「45以上60未満」の階級に属する値が45なら、2018年度の四分位範囲は30となり、2018年度の四分位範囲のほうが小さくなります。一方、「45以上60未満」の階級に属する値が55なら、2018年度の四分位範囲は40となり、2018年度の四分位範囲のほうが大きくなります。
よって、四分位範囲は大小が決まらないので、選択肢3が正解です。
解答
ケコサ:220
シス:03
解答編 つづき
(2) 各国において、学習者数を教育機関数で割ることにより、「教育機関1機関当たりの学習者数」も算出した。図3は、2009年度における「教育機関1機関あたりの学習者数」の箱ひげ図である。
2009年度について、「教育機関1機関当たりの学習者数」(横軸)と「教員1人あたりの学習者数」(縦軸)の残布図は $\dBox{セ}$ であり。ここで、2009年度における「教員1人あたりの学習者数」のヒストグラムである(1)の図1を、図4として再掲しておく。
$\dbox{セ}$ については、最も適当なものを、次の 0 ~ 3 のうちから一つ選べ。なお、これらの散布図には、完全に重なっている点はない。
解説
わかりやすいところから絞っていきます。
まず、図3の箱ひげ図を見ると、最大値は450より大きいことがわかります。このことから、散布図の中で、横軸で見たときに最大値が450を超えていない選択肢1は誤りだとわかります。
次に、図3の箱ひげ図の中央値を見てみます。150より少し小さい値だとわかります。散布図で、横軸で見たときに、上から15番目の点に注目すると、選択肢3は、中央値が150より大きいことがわかります。なので、これは誤りです。
最後に、図3の第3四分位数に着目してみます。箱ひげ図からは250より小さい値だとわかります。しかし、選択肢0の上から7番目・8番目の値はどちらも250以上なので、これも誤りだとわかります。
点が小さくてなかなか選びづらいですが、結局、選択肢2が正しいとわかります。
解答
セ:2
解答編 つづき
(3) 各国における2018年度の学習者数を $100$ としたときの2009年度の学習者数 $S$ 、および、各国における2018年度の教員数を $100$ としたときの2009年度の教員数 $T$ を算出した。
例えば、学習者数について説明すると、ある国において、2009年度が $44272$ 人、2018年度が $174521$ 人であった場合、2009年度の学習者数 $S$ は $\dfrac{44272}{174521}\times 100$ より $25.4$ と算出される。
表1は $S$ と $T$ について、平均値、標準偏差および共分散を計算したものである。ただし、 $S$ と $T$ の共分散は、 $S$ の偏差と $T$ の偏差の積の平均値である。
表1の数値が四捨五入していない正確な値であるとして、 $S$ と $T$ の相関係数を求めると $\myBox{ソ}. \myBox{タチ}$ である。
表1 平均値、標準偏差および共分散 $S$ の
平均値$T$ の
平均値$S$ の
標準偏差$T$ の
標準偏差$S$ と $T$ の
共分散$81.8$ $72.9$ $39.3$ $29.9$ $735.3$
解説
相関係数は、共分散をそれぞれの標準偏差で割ればいいので\[ \dfrac{735.3}{39.3\cdot29.9}=0.625\cdots \]となるので、解答欄に合うように四捨五入して $0.63$ が答えとなります。
解答
ソタチ:063
解答編 つづき
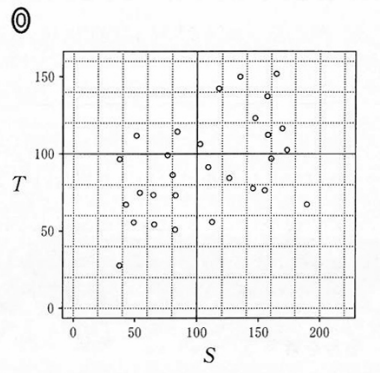
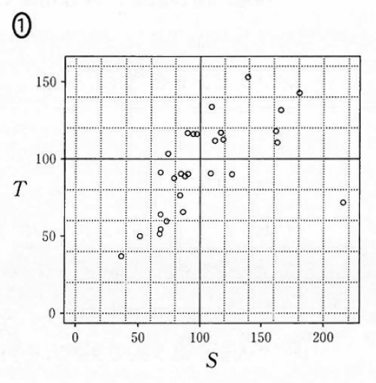
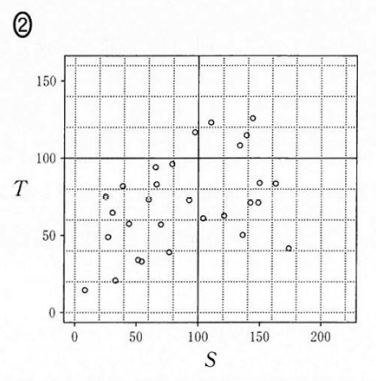
(4) 表1と(3)で求めた相関係数を参考にすると、(3)で算出した2009年度の $S$ (横軸)と $T$ (縦軸)の散布図は $\dBox{ツ}$ である。
$\dbox{ツ}$ については、最も適当なものを、次の 0 ~ 3 のうちから一つ選べ。なお、これらの散布図には、完全に重なっている点はない。
解説
まず、表1から、 $S$ も $T$ も平均は $80$ 近辺だとわかります。散布図で、 $100$ の線から原点に近い方の隣にある薄い線あたりです。この線に着目すると、選択肢0や選択肢1は平均より上や右にたくさん点があり、しかも値が大きい方に偏っているので、表1にあるような平均にはならないと考えられます。
残りは2か3ですが、相関係数が $0.63$ なので、やや強い相関があることから、2は不適なので、3が答えとなります。
ただ、選択肢3も、右下の外れ値がなければ、強い相関があるように見えます。右下の1点がなければ、相関係数は $0.8$ 程度ありそうで、この外れ値が入っただけで $0.63$ くらいに落ちるといえるか、それをこの問題の情報から確実に読み取れるかどうかは、少々あやしいです。
「相関があまりないように見えるけど実際に計算してみると実はある」なのか「相関があるように見えるけど実際に計算してみると実はそれほどない」なのか。これを選ばせるのは、微妙だと思います。
解答
ツ:3