共通テスト 数学I・数学A 2021年度 第5問 解説

【第3問～第5問から2問選択】

問題編

問題

　$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=3, \mathrm{ BC }=4, \mathrm{ AC }=5$ とする。

　$\angle \mathrm{ BAC }$ の二等分線と辺 $\mathrm{ BC }$ との交点を $\mathrm{ D }$ とすると\[ \mathrm{ BD }=\frac{\myBox{ア} }{\myBox{イ} }\ , \ \mathrm{ AD }=\frac{\myBox{ウ}\sqrt{\myBox{エ} }}{\myBox{オ} } \]である。

　また、 $\angle \mathrm{ BAC }$ の二等分線と $\triangle \mathrm{ ABC }$ の外接円 $\mathrm{ O }$ との交点で点 $\mathrm{ A }$ とは異なる点を $\mathrm{ E }$ とする。 $\triangle \mathrm{ AEC }$ に着目すると\[ \mathrm{ AE }=\myBox{カ}\sqrt{\myBox{キ} } \]である。

　$\triangle \mathrm{ ABC }$ の2辺 $\mathrm{ AB }$ と $\mathrm{ AC }$ の両方に接し、外接円 $\mathrm{ O }$ に内接する円の中心を $\mathrm{ P }$ とする。円 $\mathrm{ P }$ の半径を $r$ とする。さらに、円 $\mathrm{ P }$ と外接円 $\mathrm{ O }$ との接点を $\mathrm{ F }$ とし、直線 $\mathrm{ PF }$ と外接円 $\mathrm{ O }$ との交点で点 $\mathrm{ F }$ とは異なる点を $\mathrm{ G }$ とする。このとき\[ \mathrm{ AP }=\sqrt{\myBox{ク} }\ r \ , \ \mathrm{ PG }=\myBox{ケ}-r \]と表せる。したがって、方べきの定理により $r=\dfrac{\myBox{コ} }{\myBox{サ} }$ である。

　$\triangle \mathrm{ ABC }$ の内心を $\mathrm{ Q }$ とする。内接円 $\mathrm{ Q }$ の半径は $\myBox{シ}$ で、 $\mathrm{ AQ }=\sqrt{\myBox{ス} }$ である。また、円 $\mathrm{ P }$ と辺 $\mathrm{ AB }$ との接点を $\mathrm{ H }$ とすると、 $\mathrm{ AH }=\dfrac{\myBox{セ} }{\myBox{ソ} }$ である。

　以上から、点 $\mathrm{ H }$ に関する次の (a), (b) の正誤の組合せとして正しいものは $\myBox{タ}$ である。

　(a) 点 $\mathrm{ H }$ は3点 $\mathrm{ B,\ D,\ Q }$ を通る円の周上にある。
　(b) 点 $\mathrm{ H }$ は3点 $\mathrm{ B,\ E,\ Q }$ を通る円の周上にある。

$\mybox{タ}$ の解答群

　0: (a)正　(b)正
　1: (a)正　(b)誤
　2: (a)誤　(b)正
　3: (a)誤　(b)誤

考え方

後半になると少し図がかきづらくなりますが、過去問を解いていれば対応できるレベルでしょう。

最後の選択問題は条件を言い換えたり、それまでに求めたものをどう使うかを考えないといけないですが、図がかけていれば、何を示すべきかを考えるのはそれほど難しくはないでしょう。

解答編

問題

　$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=3, \mathrm{ BC }=4, \mathrm{ AC }=5$ とする。

　$\angle \mathrm{ BAC }$ の二等分線と辺 $\mathrm{ BC }$ との交点を $\mathrm{ D }$ とすると\[ \mathrm{ BD }=\frac{\myBox{ア} }{\myBox{イ} }\ , \ \mathrm{ AD }=\frac{\myBox{ウ}\sqrt{\myBox{エ} }}{\myBox{オ} } \]である。

解説

図は次のようになっています。

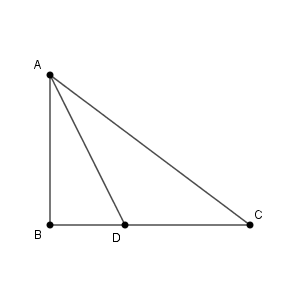
まず、 $\angle \mathrm{ B }$ が直角であることがわかります。また、 AD が角の二等分線だから、 $\mathrm{ AB:AC=BD:CD }$ が成り立つので
\begin{eqnarray} \mathrm{ BD }:(4-\mathrm{ BD }) &=& 3:5 \\[5pt] 5\mathrm{ BD } &=& 3(4-\mathrm{ BD }) \\[5pt] 8\mathrm{ BD } &=& 12 \\[5pt] \mathrm{ BD } &=& \frac{3}{2} \\[5pt] \end{eqnarray}となります。

三角形 ABD は直角三角形なので
\begin{eqnarray} \mathrm{ AD } &=& \sqrt{3^2+\left(\frac{3}{2}\right)^2} \\[5pt] &=& \sqrt{9+\frac{9}{4} } \\[5pt] &=& \frac{3\sqrt{5} }{2} \\[5pt] \end{eqnarray}と求められます。

解答

アイ：32
ウエオ：352

解答編 つづき

　また、 $\angle \mathrm{ BAC }$ の二等分線と $\triangle \mathrm{ ABC }$ の外接円 $\mathrm{ O }$ との交点で点 $\mathrm{ A }$ とは異なる点を $\mathrm{ E }$ とする。 $\triangle \mathrm{ AEC }$ に着目すると\[ \mathrm{ AE }=\myBox{カ}\sqrt{\myBox{キ} } \]である。

解説

図は次のようになっています。

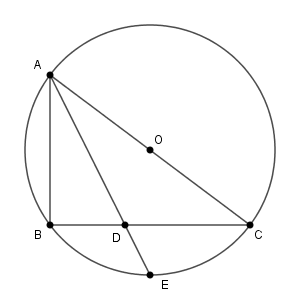
AD は $\angle \mathrm{ BAC }$ の二等分線なので、 $\angle \mathrm{ BAD }=\angle \mathrm{ EAC }$ です。また、 $\angle \mathrm{ ABC }$ も $\angle \mathrm{ AEC }$ も、直径に対する円周角なので、どちらも $90^{\circ}$ です。そのため、三角形 ABD と三角形 AEC は相似になります。

よって、
\begin{eqnarray} \mathrm{ AB:AD } &=& \mathrm{ AE:AC } \\[5pt] 3:\frac{3\sqrt{5} }{2} &=& \mathrm{ AE }:5 \\[5pt] \frac{3\sqrt{5} }{2}\cdot \mathrm{ AE } &=& 15 \\[5pt] \mathrm{ AE } &=& 15\cdot \frac{2}{3\sqrt{5} } \\[5pt] &=& 2\sqrt{5} \\[5pt] \end{eqnarray}となります。

解答

カキ：25

解答編 つづき

　$\triangle \mathrm{ ABC }$ の2辺 $\mathrm{ AB }$ と $\mathrm{ AC }$ の両方に接し、外接円 $\mathrm{ O }$ に内接する円の中心を $\mathrm{ P }$ とする。円 $\mathrm{ P }$ の半径を $r$ とする。さらに、円 $\mathrm{ P }$ と外接円 $\mathrm{ O }$ との接点を $\mathrm{ F }$ とし、直線 $\mathrm{ PF }$ と外接円 $\mathrm{ O }$ との交点で点 $\mathrm{ F }$ とは異なる点を $\mathrm{ G }$ とする。このとき\[ \mathrm{ AP }=\sqrt{\myBox{ク} }\ r \ , \ \mathrm{ PG }=\myBox{ケ}-r \]と表せる。したがって、方べきの定理により $r=\dfrac{\myBox{コ} }{\myBox{サ} }$ である。

解説

まず、 P については次のようになっています。

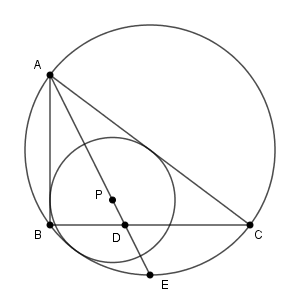
円P と辺 AB との接点を H とすると、AB と PH は垂直に交わるため、三角形 APH と三角形 ADB は相似です。

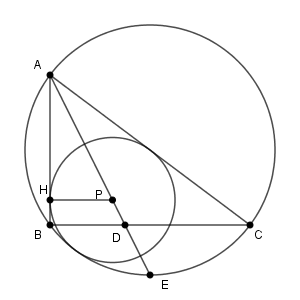
よって、
\begin{eqnarray} \mathrm{ AP:PH } &=& \mathrm{ AD:BD } \\[5pt] \mathrm{AP}:r &=& \frac{3\sqrt{5} }{2}:\frac{3}{2} \\[5pt] &=& \sqrt{5}:1 \\[5pt] \end{eqnarray}だから、 $\mathrm{ AP }=\sqrt{5}r$ となります。

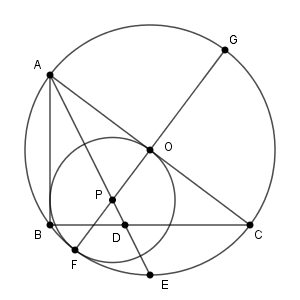
また、2円が接していることから、 F, P, O, G は同一直線上にあります（接点と円の中心は同一直線上にあります）。そのため、 PG は円 O の直径から PF の長さを引いたものになります。円 O の直径は AC と等しく $5$ なので、\[ \mathrm{ PG }=5-r \]となります。

方べきの定理から
\begin{eqnarray} \mathrm{ PA\cdot PE } &=& \mathrm{ PG\cdot PF } \\[5pt] \sqrt{5}r\cdot (\mathrm{ AE }-\mathrm{ AP }) &=& (5-r)r \\[5pt] \sqrt{5}(2\sqrt{5}-\sqrt{5}r) &=& 5-r \\[5pt] 10-5r &=& 5-r \\[5pt] -4r &=& -5 \\[5pt] r &=& \frac{5}{4} \\[5pt] \end{eqnarray}と求められます。

解答

ク：5
ケ：5
コサ：54

解答編 つづき

　$\triangle \mathrm{ ABC }$ の内心を $\mathrm{ Q }$ とする。内接円 $\mathrm{ Q }$ の半径は $\myBox{シ}$ で、 $\mathrm{ AQ }=\sqrt{\myBox{ス} }$ である。また、円 $\mathrm{ P }$ と辺 $\mathrm{ AB }$ との接点を $\mathrm{ H }$ とすると、 $\mathrm{ AH }=\dfrac{\myBox{セ} }{\myBox{ソ} }$ である。

解説

まず、 Q について考えます。

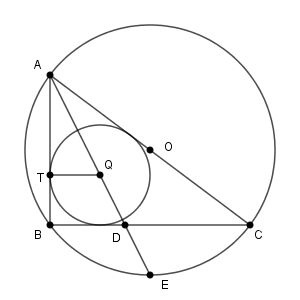
内接円の半径を求めるときによく使うのは、三角形の面積を使う方法です。三角形 ABC の面積は $\dfrac{3\cdot 4}{2}=6$ ですが、これを AQ, BQ, CQ の3つの線分で分けて3つの三角形に分割します。そうすると、内接円の半径に $3+4+5$ を掛けて2で割ったものが三角形 ABC の面積となります。こうして、内接円 Q の半径は $1$ だとわかります。

内接円 Q と辺 AB との接点を T とすると、三角形 AQT は三角形 ADB と相似です。そのため
\begin{eqnarray} \mathrm{ AQ:QT } &=& \mathrm{ AD:BD } =\sqrt{5}:1 \end{eqnarray}なので、 $\mathrm{ AQ }=\sqrt{5}$ と求められます。

AH は、三角形 APH と三角形 ADB が相似であることを使って
\begin{eqnarray} \mathrm{ AH:HP } &=& \mathrm{ AB:BD } \\[5pt] \mathrm{ AH }: \frac{5}{4} &=& 3:\frac{3}{2} \\[5pt] \mathrm{ AH }&=&\frac{5}{2} \\[5pt] \end{eqnarray}と求められます。

解答

シ：1
ス：5
セソ：52

解答編 つづき

　以上から、点 $\mathrm{ H }$ に関する次の (a), (b) の正誤の組合せとして正しいものは $\myBox{タ}$ である。

　(a) 点 $\mathrm{ H }$ は3点 $\mathrm{ B,\ D,\ Q }$ を通る円の周上にある。
　(b) 点 $\mathrm{ H }$ は3点 $\mathrm{ B,\ E,\ Q }$ を通る円の周上にある。

$\mybox{タ}$ の解答群

　0: (a)正　(b)正
　1: (a)正　(b)誤
　2: (a)誤　(b)正
　3: (a)誤　(b)誤

解説

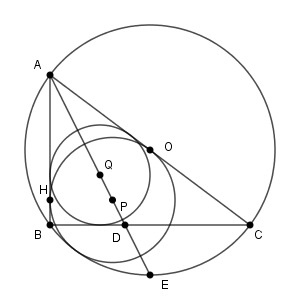
B, D, Q, H が同一円周上にある、という条件を言い換えてみましょう。今の図で使いやすそうなものは、 $\angle \mathrm{ DBH }$ が直角であることです。これを利用すれば、 $\angle \mathrm{ DQH }$ が直角であるかどうかを調べればいいです。

そのために、相似な図形を探してみます。

先ほど、 AQ, AH の長さを調べました。この比は
\begin{eqnarray} \mathrm{ AQ }:\mathrm{ AH }=\sqrt{5}:\frac{5}{2}=2:\sqrt{5} \end{eqnarray}です。また、\[ \mathrm{ AB:AD }=3:\frac{3\sqrt{5} }{2}=2:\sqrt{5} \]であり、 $\angle \mathrm{ A }$ が共通なので、三角形 AHQ と三角形 ADB は相似です。こうして、\[ \angle \mathrm{ DQH }=\angle \mathrm{ AQH }=\angle \mathrm{ ABD }=90^{\circ} \]が言えました。B, D, Q, H は同一円周上にあることがわかりました。

また、 B, E, Q, H が同一円周上にあるなら、先ほど見たように $\angle \mathrm{ DQH }=90^{\circ}$ だから $\angle \mathrm{ HBE }$ も直角となる必要がありますが、そうはならないので、この4点が同一円周上にはないことがわかります。

よって、(a)は正、(b)は誤です。

解答

タ：1