共通テスト 数学I・数学A 2021年度 第1問 [2] 解説
【必答問題】
問題編
問題
右の図のように、 $\triangle \mathrm{ ABC }$ の外側に辺 AB, BC, CA をそれぞれ1辺とする正方形 ADEB, BFGC, CHIA をかき、2点 E と F、G と H、I と D をそれぞれ線分で結んだ図形を考える。
以下において
\begin{eqnarray} & & \mathrm{ BC }=a, \ \mathrm{ CA }=b, \ \mathrm{ AB }=c \\[5pt] & & \angle \mathrm{ CAB }=A,\ \angle \mathrm{ ABC }=B,\ \angle \mathrm{ BCA }=C \end{eqnarray}とする。(1) $b=6, c=5, \cos A=\dfrac{3}{5}$ のとき、 $\sin A=\dfrac{\myBox{セ} }{\myBox{ソ} }$ であり、 $\triangle \mathrm{ ABC }$ の面積は $\myBox{タチ}$ 、$\triangle \mathrm{ AID }$ の面積は $\myBox{ツテ}$ である。
(2) 正方形 BFGC, CHIA, ADEB の面積をそれぞれ $S_1,S_2,S_3$ とする。このとき、 $S_1-S_2-S_3$ は
- $0^{\circ}\lt A\lt 90^{\circ}$ のとき、 $\myBox{ト}$。
- $A=90^{\circ}$ のとき、 $\myBox{ナ}$。
- $90^{\circ}\lt A\lt 180^{\circ}$ のとき、 $\myBox{ニ}$。
$\mybox{ト}$ ~ $\mybox{ニ}$ の解答群(同じものを繰り返し選んでもよい。)
0: 0である
1: 正の値である
2: 負の値である
3: 正の値も負の値もとる(3) $\triangle \mathrm{ AID }, \triangle \mathrm{ BEF}, \triangle \mathrm{ CGH }$ の面積をそれぞれ $T_1, T_2, T_3$ とする。このとき、 $\myBox{ヌ}$ である。
$\mybox{ヌ}$ の解答群
0: $a\lt b\lt c$ ならば $T_1\gt T_2 \gt T_3$
1: $a\lt b\lt c$ ならば $T_1\lt T_2 \lt T_3$
2: $A$ が鈍角ならば、 $T_1\lt T_2$ かつ $T_1\lt T_3$
3: $a,b,c$ の値に関係なく、 $T_1=T_2=T_3$(4) $\triangle \mathrm{ ABC }$, $\triangle \mathrm{ AID }$, $\triangle \mathrm{ BEF }$, $\triangle \mathrm{ CGH }$ のうち、外接円の半径が最も小さいものを求める。
$0^{\circ}\lt A\lt 90^{\circ}$ のとき、 $\mathrm{ ID }$ $\myBox{ネ}$ $\mathrm{ BC }$ であり
($\triangle \mathrm{ AID }$ の外接円の半径) $\myBox{ノ}$ ($\triangle \mathrm{ ABC }$ の外接円の半径)
であるから、外接円の半径が最も小さい三角形は
- $0^{\circ}\lt A\lt B \lt C \lt 90^{\circ}$ のとき、 $\myBox{ハ}$ である。
- $0^{\circ}\lt A\lt B \lt 90^{\circ} \lt C$ のとき、 $\myBox{ヒ}$ である。
$\mybox{ネ}, \mybox{ノ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\lt$
1: $=$
2: $\gt$$\mybox{ハ}, \mybox{ヒ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\triangle \mathrm{ ABC }$
1: $\triangle \mathrm{ AID }$
2: $\triangle \mathrm{ BEF }$
3: $\triangle \mathrm{ CGH }$
考え方
ほとんど計算はないですが、図形から情報を読み取り、補角の公式、余弦定理、正弦定理を応用して考えないといけません。
(2)は、 $a,b,c$ で表してみたほうがわかりやすいかもしれません。(3)は、(1)をヒントに考えましょう。(4)は、向かい合う角を利用して、外接円の半径との関係性を考えましょう。
解答編
問題
右の図のように、 $\triangle \mathrm{ ABC }$ の外側に辺 AB, BC, CA をそれぞれ1辺とする正方形 ADEB, BFGC, CHIA をかき、2点 E と F、G と H、I と D をそれぞれ線分で結んだ図形を考える。
以下において
\begin{eqnarray} & & \mathrm{ BC }=a, \ \mathrm{ CA }=b, \ \mathrm{ AB }=c \\[5pt] & & \angle \mathrm{ CAB }=A,\ \angle \mathrm{ ABC }=B,\ \angle \mathrm{ BCA }=C \end{eqnarray}とする。(1) $b=6, c=5, \cos A=\dfrac{3}{5}$ のとき、 $\sin A=\dfrac{\myBox{セ} }{\myBox{ソ} }$ であり、 $\triangle \mathrm{ ABC }$ の面積は $\myBox{タチ}$ 、$\triangle \mathrm{ AID }$ の面積は $\myBox{ツテ}$ である。
解説
三角比の相互関係から \[\sin^2 A=1-\cos^2 A=\frac{16}{25}\]なので、 $\sin A=\dfrac{4}{5}$ です。
これより、 $\triangle \mathrm{ ABC }$ の面積は
\begin{eqnarray}
\frac{bc}{2}\sin A=\frac{6\cdot 5}{2}\cdot \frac{4}{5}=12
\end{eqnarray}と求められます。
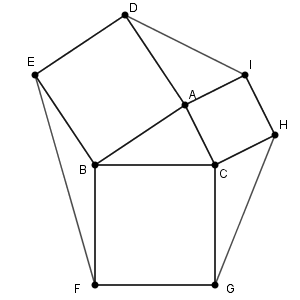
$\triangle \mathrm{ AID }$ の面積は、 $\mathrm{ AI }=b=6$, $\mathrm{ AD }=c=5$ と $\angle \mathrm{ DAI }=180^{\circ}-A$ より
\begin{eqnarray}
\frac{\mathrm{ AI }\cdot\mathrm{ AD } }{2}\sin (180^{\circ}-A)=\frac{bc}{2}\sin A=12
\end{eqnarray}と求められます。ここでは、補角の公式、つまり、 $\sin(180^{\circ}-\theta)=\sin\theta$ となることを使っています。(参考:【基本】補角の三角比)
解答
セソ:45
タチ:12
ツテ:12
解答編 つづき
(2) 正方形 BFGC, CHIA, ADEB の面積をそれぞれ $S_1,S_2,S_3$ とする。このとき、 $S_1-S_2-S_3$ は
- $0^{\circ}\lt A\lt 90^{\circ}$ のとき、 $\myBox{ト}$。
- $A=90^{\circ}$ のとき、 $\myBox{ナ}$。
- $90^{\circ}\lt A\lt 180^{\circ}$ のとき、 $\myBox{ニ}$。
$\mybox{ト}$ ~ $\mybox{ニ}$ の解答群(同じものを繰り返し選んでもよい。)
0: 0である
1: 正の値である
2: 負の値である
3: 正の値も負の値もとる
解説
$S_1$, $S_2$, $S_3$ は、それぞれ、 $a^2$, $b^2$, $c^2$ と書けます。なので、 $S_1-S_2-S_3$ は、 $a^2-b^2-c^2$ のことです。
余弦定理より、 $a^2=b^2+c^2-2bc\cos A$ が成り立つので、 $a^2-b^2-c^2$ とは $-2bc\cos A$ のことです。
以上から、 $0^{\circ}\lt A\lt 90^{\circ}$ のときは、 $\cos A$ は正なので、 $-2bc\cos A$ は負となります。
$A=90^{\circ}$ のときは $-2bc\cos A$ は $0$ となり、鈍角のときは正となります。
解答
ト:2
ナ:0
ニ:1
解答編 つづき
(3) $\triangle \mathrm{ AID }, \triangle \mathrm{ BEF}, \triangle \mathrm{ CGH }$ の面積をそれぞれ $T_1, T_2, T_3$ とする。このとき、 $\myBox{ヌ}$ である。
$\mybox{ヌ}$ の解答群
0: $a\lt b\lt c$ ならば $T_1\gt T_2 \gt T_3$
1: $a\lt b\lt c$ ならば $T_1\lt T_2 \lt T_3$
2: $A$ が鈍角ならば、 $T_1\lt T_2$ かつ $T_1\lt T_3$
3: $a,b,c$ の値に関係なく、 $T_1=T_2=T_3$
解説

$\triangle \mathrm{ AID }$ の面積は、 $\dfrac{\mathrm{ AI }\cdot \mathrm{ AD } }{2}\sin \angle \mathrm{ DAI }$ となりますが、これは(1)で見たように、 $\dfrac{bc}{2}\sin A$ と等しくなります。
同じように計算すると、 $\triangle \mathrm{BEF}$ の面積は $\dfrac{\mathrm{ BE }\cdot \mathrm{ BF } }{2}\sin \angle \mathrm{ EBF }$ となりますが、これは $\dfrac{ca}{2}\sin B$ と等しくなります。
また、 $\triangle \mathrm{CGH}$ の面積は $\dfrac{\mathrm{ CG }\cdot \mathrm{ CH } }{2}\sin \angle \mathrm{ GCH }$ となりますが、これは $\dfrac{ab}{2}\sin C$ と等しくなります。
つまり、どの三角形も、三角形 ABC の面積と等しくなります。こうして、 $T_1=T_2=T_3$ であることがわかります。
解答
ヌ:3
解答編 つづき
(4) $\triangle \mathrm{ ABC }$, $\triangle \mathrm{ AID }$, $\triangle \mathrm{ BEF }$, $\triangle \mathrm{ CGH }$ のうち、外接円の半径が最も小さいものを求める。
$0^{\circ}\lt A\lt 90^{\circ}$ のとき、 $\mathrm{ ID }$ $\myBox{ネ}$ $\mathrm{ BC }$ であり
($\triangle \mathrm{ AID }$ の外接円の半径) $\myBox{ノ}$ ($\triangle \mathrm{ ABC }$ の外接円の半径)
であるから、外接円の半径が最も小さい三角形は
- $0^{\circ}\lt A\lt B \lt C \lt 90^{\circ}$ のとき、 $\myBox{ハ}$ である。
- $0^{\circ}\lt A\lt B \lt 90^{\circ} \lt C$ のとき、 $\myBox{ヒ}$ である。
$\mybox{ネ}, \mybox{ノ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\lt$
1: $=$
2: $\gt$$\mybox{ハ}, \mybox{ヒ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\triangle \mathrm{ ABC }$
1: $\triangle \mathrm{ AID }$
2: $\triangle \mathrm{ BEF }$
3: $\triangle \mathrm{ CGH }$
解説

ID と BC の長さについて考えましょう。三角形 ABC と三角形 AID について考えると、 AB=AD, AC=AI が成り立つので、角が大きいほど対辺も長くなります(余弦定理を使っても示せます)。
そのため、 $0^{\circ}\lt A \lt 90^{\circ}$ の場合は、 $\angle \mathrm{ DAI }\gt A$ なので、\[ \mathrm{ ID }\gt \mathrm{ BC } \]が成り立ちます。
三角形 ABC の外接円の半径を $R$ とすると、正弦定理から $2R=\dfrac{\mathrm{ BC } }{\sin A}$ となります。また、三角形 ADI の外接円の半径を $R'$ とすると、 $2R'=\dfrac{\mathrm{ ID } }{\sin \angle \mathrm{ DAI } }$ となりますが、補角の公式からこの $\sin $ は同じ値です。つまり、 $\mathrm{ ID } \gt \mathrm{ BC }$ から $R'\gt R$ も言えます。
同様に考えると、 $0^{\circ}\lt A\lt B \lt C \lt 90^{\circ}$ の場合は、三角形 ABC の外接円の半径は、まわりの3つの三角形のどの外接円の半径よりも小さくなるので、外接円の半径が最も小さい三角形は $\triangle \mathrm{ ABC }$ です。
最後に、 $C$ が鈍角の場合を考えます。
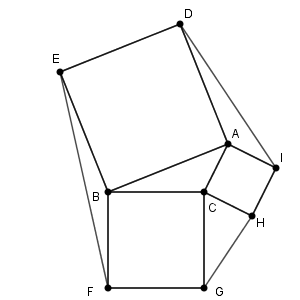
今まで見てきたように、向かい合う角の小さい方が外接円の半径も小さくなることを考えると、三角形 ABC と三角形 CGH では、後者の方が外接円の半径が小さくなることがわかります。
解答
ネ:2
ノ:2
ハ:0
ヒ:3





