共通テスト数学I・数学A 2021年度第2問 [2] 解説

🕒 2021/01/19 🔄 2023/05/01

【必答問題】

問題編

問題

　就業者の従事する産業は、勤務する事務所の主な経済活動の種類によって、第１次産業（農業、林業と漁業）、第２次産業（鉱業、建設業と製造業）、第３次産業（前記以外の産業）の三つに分類される。国の労働状況の調査（国勢調査）では、47の都道府県別に第１次、第２次、第３次それぞれの産業ごとの就業者数が発表されている。ここでは都道府県別に、就業者数に対する各産業に就業する人数の割合を算出したものを、各産業の「就業者数割合」と呼ぶことにする。

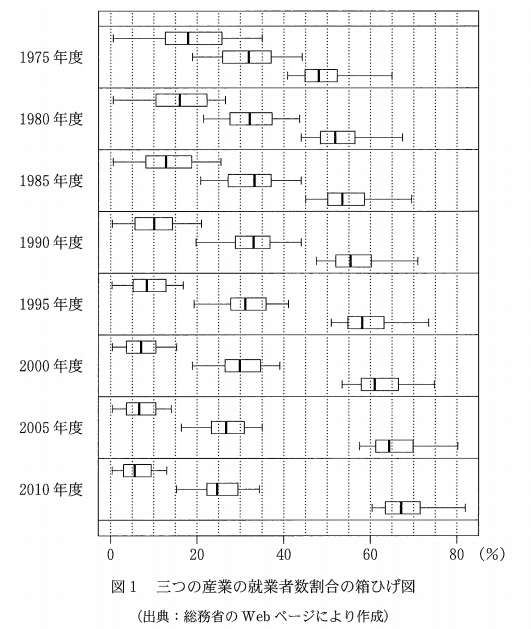
　(1) 図１は、1975年度から2010年度まで５年ごとの８個の年度（それぞれを時点という）における都道府県別の三つの産業の就業者数割合を箱ひげ図で表したものである。各時点の箱ひげ図は、それぞれ上から順に第１次産業、第２次産業、第３次産業のものである。

　次の 0 ～ 5 のうち、図１から読み取れることとして正しくないものは $\dBox{タ}$ と $\dBox{チ}$ である。

$\dbox{タ}$, $\dbox{チ}$ の解答群（解答の順序は問わない。）

　0: 第１次産業の就業者数割合の四分位範囲は、2000年度までは、後の時点になるにしたがって減少している。

　1: 第１次産業の就業者数割合について、左側のひげの長さと右側のひげの長さを比較すると、どの時点においても左側の方が長い。

　2: 第２次産業の就業者数割合の中央値は、1990年度以降、後の時点になるにしたがって減少している。

　3: 第２次産業の就業者数割合の第１四分位数は、後の時点になるにしたがって減少している。

　4: 第３次産業の就業者数割合の第３四分位数は、後の時点になるにしたがって増加している。

　5: 第３次産業の就業者数割合の最小値は、後の時点になるにしたがって増加している。

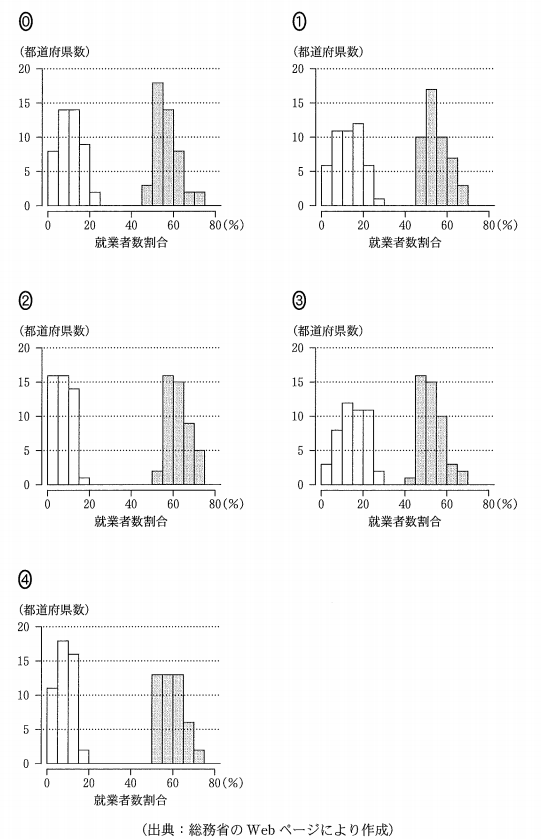
(2) (1)で取り上げた８時点の中から５時点を取り出して考える。各時点における都道府県別の第１次産業と第３次産業の就業者数割合のヒストグラムを一つのグラフにまとめてかいたものが、次ページの五つのグラフである。それぞれの右側の網掛けしたヒストグラムが第３次産業のものである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　・1985年度におけるグラフは $\dBox{ツ}$ である。

　・1995年度におけるグラフは $\dBox{テ}$ である。

$\dbox{ツ}$, $\dbox{テ}$ については、最も適当なものを、ツの 0 ～ 4 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

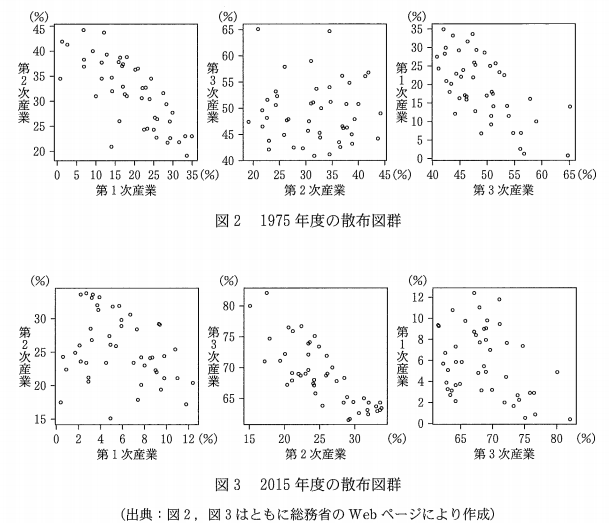
(3) 三つの産業から二つずつを組み合わせて都道府県別の就業者数割合の散布図を作成した。図２の散布図群は、左から順に1975年度における第１次産業（横軸）と第２次産業（縦軸）の散布図、第２次産業（横軸）と第３次産業（縦軸）の散布図、および第３次産業（横軸）と第１次産業（縦軸）の散布図である。また、図３は同様に作成した2015年度の散布図群である。

　下の(I)、(II)、(III)は、1975年度を基準としたときの、2015年度の変化を記述したものである。ただし、ここで「相関が強くなった」とは、相関係数の絶対値が大きくなったことを意味する。

　(I) 都道府県別の第１次産業の就業者割合と第２次産業の就業者数割合の間の相関は強くなった。

　(II) 都道府県別の第２次産業の就業者割合と第３次産業の就業者数割合の間の相関は強くなった。

　(III) 都道府県別の第３次産業の就業者割合と第１次産業の就業者数割合の間の相関は強くなった。

　(I)、(II)、(III)の正誤の組合せとして正しいものは $\dBox{ト}$ である。

$\dbox{ト}$ の解答群

　0: (I) 正　(II) 正　(III) 正
　1: (I) 正　(II) 正　(III) 誤
　2: (I) 正　(II) 誤　(III) 正
　3: (I) 正　(II) 誤　(III) 誤
　4: (I) 誤　(II) 正　(III) 正
　5: (I) 誤　(II) 正　(III) 誤
　6: (I) 誤　(II) 誤　(III) 正
　7: (I) 誤　(II) 誤　(III) 誤

(4) 各都道府県の就業者数の内訳として男女別の就業者数も発表されている。そこで、就業者数に対する男性・女性の就業者数の割合をそれぞれ「男性の就業者数割合」、「女性の就業者数割合」と呼ぶことにし、これらを都道府県別に算出した。図４は、2015年度における都道府県別の、第１次産業の就業者数割合（横軸）と、男性の就業者数割合（縦軸）の散布図である。

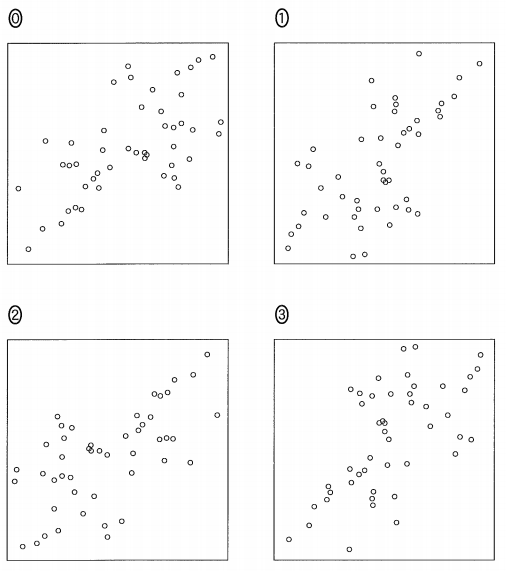
　各都道府県の、男性の就業者数と女性の就業者数を合計すると就業者数の全体となることに注意すると、2015年度における都道府県別の、第１次産業の就業者数割合（横軸）と、女性の就業者数割合（横軸）の散布図は $\dBox{ナ}$ である。

　$\dbox{ナ}$ については、最も適当なものを、下の 0 ～ 3 のうちから一つ選べ。なお、設問の都合で各散布図の横軸と縦軸の目盛りは省略しているが、横軸は右方向、縦軸は上方向がそれぞれ正の方向である。

考え方

ヒストグラムを選ぶ問題が少し難しい（2つにしぼれるが1つにしぼるのが大変）ですが、それ以外の問題は、言葉の定義や言葉の意味するところを理解していれば解けるでしょう。ヒストグラムを選ぶ問題は、各ヒストグラムや各箱ひげ図でどこに差があるかに注目しながら選んでいきましょう。

解答編

問題

　就業者の従事する産業は、勤務する事務所の主な経済活動の種類によって、第１次産業（農業、林業と漁業）、第２次産業（鉱業、建設業と製造業）、第３次産業（前記以外の産業）の三つに分類される。国の労働状況の調査（国勢調査）では、47の都道府県別に第１次、第２次、第３次それぞれの産業ごとの就業者数が発表されている。ここでは都道府県別に、就業者数に対する各産業に就業する人数の割合を算出したものを、各産業の「就業者数割合」と呼ぶことにする。

　(1) 図１は、1975年度から2010年度まで５年ごとの８個の年度（それぞれを時点という）における都道府県別の三つの産業の就業者数割合を箱ひげ図で表したものである。各時点の箱ひげ図は、それぞれ上から順に第１次産業、第２次産業、第３次産業のものである。

　次の 0 ～ 5 のうち、図１から読み取れることとして正しくないものは $\dBox{タ}$ と $\dBox{チ}$ である。

$\dbox{タ}$, $\dbox{チ}$ の解答群（解答の順序は問わない。）

　0: 第１次産業の就業者数割合の四分位範囲は、2000年度までは、後の時点になるにしたがって減少している。

　1: 第１次産業の就業者数割合について、左側のひげの長さと右側のひげの長さを比較すると、どの時点においても左側の方が長い。

　2: 第２次産業の就業者数割合の中央値は、1990年度以降、後の時点になるにしたがって減少している。

　3: 第２次産業の就業者数割合の第１四分位数は、後の時点になるにしたがって減少している。

　4: 第３次産業の就業者数割合の第３四分位数は、後の時点になるにしたがって増加している。

　5: 第３次産業の就業者数割合の最小値は、後の時点になるにしたがって増加している。

解説

一つずつ選択肢を確認していきます。

0について。四分位範囲とは、第３四分位数と第１四分位との差のことで、図でいうと、箱の長さのことです。第１次産業の箱ひげ図を見ると、2000年度までは確かに短くなっているので、正しいです。

1について。ひげとは、図でいうと、箱から出ている線のことです。問題文では「どの時点でも左の方が長い」となっていますが、1990年度や2010年度を見ると、右のほうが長くなっています。なので、正しくありません。

2について、中央値は、図でいうと箱の中にある縦線のことです。第２次産業の中央値は、たしかに1990年度以降、減少していることがわかります。正しいです。

3について、第１四分位数は、箱の左側のことです。1990年度ごろまでは増えているので、問題文の「後の時点になるにしたがって減少している」は正しくありません。

4について、第３四分位数は、箱の右側のことです。第３次産業の箱ひげ図を見ると、たしかに増加していることがわかります。正しいです。

5について、最小値とは箱ひげ図の左端のことです。これも、後の時点になるにしたがって増加しています。正しいです。

以上より、1と3が答えです。

解答

タ：チ：1・3

解答編つづき

(2) (1)で取り上げた８時点の中から５時点を取り出して考える。各時点における都道府県別の第１次産業と第３次産業の就業者数割合のヒストグラムを一つのグラフにまとめてかいたものが、次ページの五つのグラフである。それぞれの右側の網掛けしたヒストグラムが第３次産業のものである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　・1985年度におけるグラフは $\dBox{ツ}$ である。

　・1995年度におけるグラフは $\dBox{テ}$ である。

$\dbox{ツ}$, $\dbox{テ}$ については、最も適当なものを、ツの 0 ～ 4 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

解説

1985年度の箱ひげ図を見ると、第１次産業は、最小値はほぼ0、最大値は25より少し大きい値だとわかります。第３次産業は、最小値がほぼ45、最大値が70弱だとわかります。

そこで、ヒストグラムを見てみると、第１次産業の最大値が25～30の範囲になっているものを選ぶと、1と3が残ります。この2つはとてもよく似ていますが、第３次産業の最小値が40～45なのか、45～50なのか、という違いがあります。

これをもとにもう一度箱ひげ図を見てみると、第１次産業の最大値が25～30となっているのは、1980年度と1985年度の2つしかなく、1980年度の第３次産業の最小値が明確に45未満となっています。

こうして、1980年度のヒストグラムが3で、ツに入る1985年度のヒストグラムが1だと特定できます。

次に、1995年度です。箱ひげ図を見ると、第１次産業は、最小値はほぼ0、最大値は15～20の範囲わかります。第３次産業は、最小値が50より少し大きい値、最大値が75弱だとわかります。

ヒストグラムを見ると、第１次産業の最小値から、2か4にしぼられます。この2つは、第１次産業も第３次産業も最大値と最小値の階級が同じなので、他の要素を考えないといけません。

箱ひげ図に戻ると、第１次産業の最大値が15～20となっているのは、1995年度と2000年度の２つだけです。箱ひげ図で明確に違うのは第３次産業の中央値です。1995年度の中央値は55～60の階級です。

これをもとにもう一度ヒストグラムを見ると、47個のデータ（47都道府県）の中央値、つまり、下から24番目が55～60の階級に属しているものは、4のヒストグラムだとわかります。

解答

ツ：1
テ：4

解答編つづき

(3) 三つの産業から二つずつを組み合わせて都道府県別の就業者数割合の散布図を作成した。図２の散布図群は、左から順に1975年度における第１次産業（横軸）と第２次産業（縦軸）の散布図、第２次産業（横軸）と第３次産業（縦軸）の散布図、および第３次産業（横軸）と第１次産業（縦軸）の散布図である。また、図３は同様に作成した2015年度の散布図群である。

　下の(I)、(II)、(III)は、1975年度を基準としたときの、2015年度の変化を記述したものである。ただし、ここで「相関が強くなった」とは、相関係数の絶対値が大きくなったことを意味する。

　(I) 都道府県別の第１次産業の就業者割合と第２次産業の就業者数割合の間の相関は強くなった。

　(II) 都道府県別の第２次産業の就業者割合と第３次産業の就業者数割合の間の相関は強くなった。

　(III) 都道府県別の第３次産業の就業者割合と第１次産業の就業者数割合の間の相関は強くなった。

　(I)、(II)、(III)の正誤の組合せとして正しいものは $\dBox{ト}$ である。

$\dbox{ト}$ の解答群

　0: (I) 正　(II) 正　(III) 正
　1: (I) 正　(II) 正　(III) 誤
　2: (I) 正　(II) 誤　(III) 正
　3: (I) 正　(II) 誤　(III) 誤
　4: (I) 誤　(II) 正　(III) 正
　5: (I) 誤　(II) 正　(III) 誤
　6: (I) 誤　(II) 誤　(III) 正
　7: (I) 誤　(II) 誤　(III) 誤

解説

相関が強くなった、というのは、散布図でいうと、より直線的に分布するようになった、ということです。2015年度のほうがより直線的になったものは、真ん中だけです。左側も右側も、2015年度のほうが、直線からはなれているように分布しています。

そのため、誤・正・誤なので、5が答えです。

解答

ト：5

解答編つづき

(4) 各都道府県の就業者数の内訳として男女別の就業者数も発表されている。そこで、就業者数に対する男性・女性の就業者数の割合をそれぞれ「男性の就業者数割合」、「女性の就業者数割合」と呼ぶことにし、これらを都道府県別に算出した。図４は、2015年度における都道府県別の、第１次産業の就業者数割合（横軸）と、男性の就業者数割合（縦軸）の散布図である。

　各都道府県の、男性の就業者数と女性の就業者数を合計すると就業者数の全体となることに注意すると、2015年度における都道府県別の、第１次産業の就業者数割合（横軸）と、女性の就業者数割合（横軸）の散布図は $\dBox{ナ}$ である。

　$\dbox{ナ}$ については、最も適当なものを、下の 0 ～ 3 のうちから一つ選べ。なお、設問の都合で各散布図の横軸と縦軸の目盛りは省略しているが、横軸は右方向、縦軸は上方向がそれぞれ正の方向である。