京都大学 理系 2021年度 第5問 解説
問題編
問題
$xy$ 平面において、2点 $\mathrm{ B }(-\sqrt{3},-1)$, $\mathrm{ C }(\sqrt{3},-1)$ に対し、点 A は次の条件(*)を満たすとする。
(*) $\angle \mathrm{ BAC }=\dfrac{\pi}{3}$ かつ点 A の $y$ 座標は正
次の各問に答えよ。
(1) $\triangle \mathrm{ ABC }$ の外心の座標を求めよ。
(2) 点 A が条件(*)を満たしながら動くとき、 $\triangle \mathrm{ ABC }$ の垂心の軌跡を求めよ。
考え方
(1)は、外心は $y$ 軸上にあることがわかるので、それほど計算がごちゃごちゃしないで求めることができます。一方、(2)は少し計算がごちゃつきますが、計算を頑張ればきれいな答えが得られます。
なお、別解で、幾何的に解く方法も追加しています。
解答編
問題
$xy$ 平面において、2点 $\mathrm{ B }(-\sqrt{3},-1)$, $\mathrm{ C }(\sqrt{3},-1)$ に対し、点 A は次の条件(*)を満たすとする。
(*) $\angle \mathrm{ BAC }=\dfrac{\pi}{3}$ かつ点 A の $y$ 座標は正
次の各問に答えよ。
(1) $\triangle \mathrm{ ABC }$ の外心の座標を求めよ。
解答例
(1)
点 A が $y$ 軸上にあるとき、三角形 ABC は $y$ 軸について対称な正三角形となる。1辺が $2\sqrt{3}$ なので高さは $3$ だから、このときの点 A の座標は $(0,2)$ である。正三角形のとき、外心と重心は一致するので、外心の座標は原点である。
点 A が条件(*)を満たすとき、円周角の定理の逆から、この外接円の上を動く。よって、三角形 ABC の外心の座標は、 $(0,0)$ である。
(終)
解答編 続き
問題
(2) 点 A が条件(*)を満たしながら動くとき、 $\triangle \mathrm{ ABC }$ の垂心の軌跡を求めよ。
解答例
点 $\mathrm{ A }(a,b)$ とする。点 A は、 $a^2+b^2=4$ かつ $b\gt 0$ を満たす範囲全体を動く。
$a\ne \sqrt{3}$ のとき、直線 AC の方程式は
\begin{eqnarray}
y &=& \frac{b+1}{a-\sqrt{3} }(x-\sqrt{3})-1
\end{eqnarray}なので、点 B から直線 AC に下した垂線の方程式は
\begin{eqnarray}
y &=& -\frac{a-\sqrt{3} }{b+1}(x+\sqrt{3})-1
\end{eqnarray}と書くことができる。なお、この垂線の方程式は $a=\sqrt{3}$ のときもこの式で表すことができる。
これと直線 $x=a$ との交点が垂心なので、垂心の $y$ 座標は
\begin{eqnarray}
y &=& -\frac{a-\sqrt{3} }{b+1}(a+\sqrt{3})-1 \\[5pt]
&=& -\frac{a^2-3}{b+1}-1 \\[5pt]
&=& -\frac{(4-b^2)-3}{b+1}-1 \\[5pt]
&=& \frac{b^2-1}{b+1}-1 \\[5pt]
&=& b-2
\end{eqnarray}となる。よって、垂心の座標を $(X,Y)$ とおくと、 $a=X$, $b=Y+2$ なので、 $X,Y$ は $X^2+(Y+2)^2=4$ かつ $Y\gt -2$ を満たす範囲全体を動く。よって、垂心の軌跡は次のようになる。ただし、境界の点は含まない。
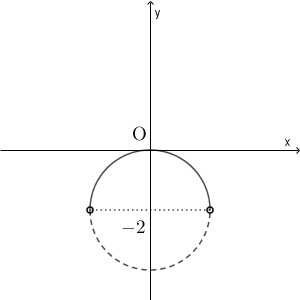
(終)
別解
幾何的に解くこともできます。垂心を H とします。
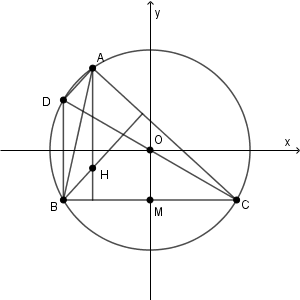
BC の中点を M とすると、 OM の長さは $1$ です。CO を伸ばして、 CD が直径となるようにすると、 OM と DB は平行で、 CD は CO の2倍なので、 $\mathrm{ DB }=2\mathrm{ OM }=2$ です。
また、 AH と BD はともに BC に垂直なので2つの線分は平行であり、 BH と DA はともに AC に垂直なので2つの線分は平行だから、四角形 AHBD は平行四辺形です。なので、 $\mathrm{ AH }=\mathrm{ BD }=2$ です。そのため、点 A の軌跡を、 $y$ 軸方向に $-2$ だけ平行移動したものが H の軌跡となります。





